Энтропия как количественная мера беспорядка в системе. Статистическая интерпретация энтропии. Микро и микросостояния системы
. Энтропия (Э) системы как количественная мера беспорядка системы определяется числом допустимых состояний (S) системы. Поэтому энтропию определяют как натуральный логарифм числа допустимых состояний системы, т.е. Э = 1nS. Энтропия системы тем больше, чем больше число допустимых состояний системы. При S =1, Э ≡ 1n1=0, а при S = SMaKC, Э ≡ lnSMакс = Эмакс.
Изолированная, или закрытая, система А3, состоящая из двух закрытых, или изолированных (не контактирующих), систем А1 и А2 (рис. 2.1) будет иметь S1 · S2 число допустимых состояний, где S1 -число допустимых состояний системы A1, a S2 - системы А2. Тогда
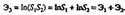 Всякая закрытая, или изолированная, система (A1, A2, A3) стремится к равновесному состоянию, когда число допустимых состояний системы максимально (Sмакс) и, следовательно, их энтропия тоже максимальна (Эмакс). Точнее, энтропия любой изолированной системы с подавляющей вероятностью со временем будет возрастать или, в крайнем случае, останется постоянной, т.е. ∆Э ≥ 0.Статистическая энтропия, определяемая по эмпирической реализации x=x1,x2,…xnнекоторого случайного процесса. Если pi — эмпирическая частота значения yi, то энтропия определяется по аналогии со случайной величиной:
Всякая закрытая, или изолированная, система (A1, A2, A3) стремится к равновесному состоянию, когда число допустимых состояний системы максимально (Sмакс) и, следовательно, их энтропия тоже максимальна (Эмакс). Точнее, энтропия любой изолированной системы с подавляющей вероятностью со временем будет возрастать или, в крайнем случае, останется постоянной, т.е. ∆Э ≥ 0.Статистическая энтропия, определяемая по эмпирической реализации x=x1,x2,…xnнекоторого случайного процесса. Если pi — эмпирическая частота значения yi, то энтропия определяется по аналогии со случайной величиной:
H=-SUM{pilog(pi) | i=1,…n};Микро- и макросостоянияМикросостояние — это состояние системы, определяемое одновременным заданием координат и импульсов всех составляющих систему частиц. Знание микросостояния в некоторый момент времени позволяет однозначно предсказать эволюцию системы во все последующие моменты. Макросостояние — это состояние системы, характеризуемое небольшим числом макроскопических параметров. Одно макросостояние может быть реализовано большим числом микросостояний за счет перестановки частиц, не меняющей наблюдаемого состояния. Статистическое описание больших систем существенно опирается на следующие постулаты. 1. Все разрешенные микросостояния равновероятны. 2. Термодинамически равновесным является то макросостояние, которое реализуется наибольшим числом микросостояний, т. е. является наиболее вероятным состоянием
46. Распределение молекул газа по скоростям. Распределение Максвелла.Скорости молекул газа имеют различные значения и направления, причем из-за огромного числа соударений, которые ежесекундно испытывает молекула, скорость ее постоянно изменяеться. Поэтому нельзя определить число молекул, которые обладают точно заданной скоростью v в данный момент времени, но можно подсчитать число молекул, скорости которых имеют значение, лежащие между некоторыми скоростями v1 и v2 . На основании теории вероятности Максвелл установил закономерность, по которой можно определить число молекул газа, скорости которых при данной температуре заключены в некотором интервале скоростей. Согласно распределению Максвелла, вероятное число молекул в единице объема; компоненты скоростей которых лежат в интервале от 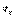 до
до 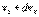 , от
, от 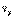 до
до 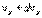 и от
и от 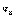 до
до 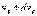 , определяются функцией распределения Максвелла
, определяются функцией распределения Максвелла 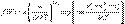 где m - масса молекулы, n - число молекул в единице объема. Отсюда следует, чтсг число молекул, абсолютные значения скоростей которых лежат в интервале от v до v + dv, имеет вид
где m - масса молекулы, n - число молекул в единице объема. Отсюда следует, чтсг число молекул, абсолютные значения скоростей которых лежат в интервале от v до v + dv, имеет вид 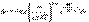
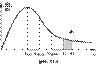 Распределение Максвелла достигает максимума при скорости Распределение Максвелла достигает максимума при скорости 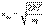 , т.е. такой скорсти, к которой близки скорости большинства молекул. Площадь заштрихованной полоски с основанием dV покажет, какая часть от общего числа молекул имеет скорости, лежащие в данном интервале. Конкретный вид функции распределения Максвелла зависит от рода газа (массы молекулы) и температуры. Давление и объем газа на распределение молекул по скоростям не влияет.Кривая распределения Максвелла позволит найти среднюю арифметическую скорость. , т.е. такой скорсти, к которой близки скорости большинства молекул. Площадь заштрихованной полоски с основанием dV покажет, какая часть от общего числа молекул имеет скорости, лежащие в данном интервале. Конкретный вид функции распределения Максвелла зависит от рода газа (массы молекулы) и температуры. Давление и объем газа на распределение молекул по скоростям не влияет.Кривая распределения Максвелла позволит найти среднюю арифметическую скорость. 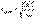 Таким образом, Таким образом, 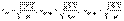 |
С Повышением температуры наиболее вероятная скорость возрастает, поэтому максимум распределения молекул по скоростям сдвигается в сторону больших скоростей, а его абсолютная величина уменьшается. Следовательно, при нагревании газа доля молекул, обладающих малыми скоростями уменьшается, а доля молекул с большими скоростями увеличивается.
47. Барометрическая формула. Распределение Больцмана. Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести. Для идеального газа, имеющего постоянную температуру T и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного паденияg одинаково), барометрическая формула имеет следующий вид: 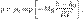 где p — давление газа в слое, расположенном на высоте h, p0 — давление на нулевом уровне (h = h0), M — молярная масса газа, R — газовая постоянная, T — абсолютная температура. Из барометрической формулы следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону:
где p — давление газа в слое, расположенном на высоте h, p0 — давление на нулевом уровне (h = h0), M — молярная масса газа, R — газовая постоянная, T — абсолютная температура. Из барометрической формулы следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону: 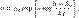 где m — масса молекулы газа, k — постоянная Больцмана.
где m — масса молекулы газа, k — постоянная Больцмана.
В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с закономраспределения Больцмана:n = n0exp( -mgh / kT )где n - концентрация молекул на высоте h, n0 - концентрация молекул на начальном уровне h = 0, m - масса частиц, g - ускорение свободного падения, k - постоянная Больцмана, T - температура.Мы можем видеть, что концентрация молекул у дна сосуда оказывается выше, чем концентрация в верхней части сосуда. Под действием теплового движения молекулы подбрасываются вверх, а затем падают вниз за счет действия сил тяжести.Если высота сосуда много меньше чем kT/mg, то зависимостью концентрации от высоты можно пренебречь. С другой стороны, в атмосфере концентрация молекул быстро уменьшается с увеличением высоты и, поэтому, величина атмосферного давления также уменьшается. Принимая во внимание, что P = nkT, мы можем записать так называемую барометрическую формулу, описывающую изменение атмосферного давления в зависимости от высоты:P = P0exp( -mgh / kT )Измеряя давление за бортом самолёта, мы можем вычислить при помощи барометрической формулы приблизительную высоту полёта.
48. Свободные затухающие колебания. Характеристики затухания: коэффициент затухания, время, релаксация, декремент затухания, добротность колебательной системы.Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Закон затухания колебаний зависит от свойств колебательной системы. Система называется линейной, если параметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса. Свободные затухающие колебания линейной системы описываются уравнением:
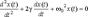 где
где 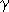 - коэффициент затухания,
- коэффициент затухания, 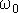 - собственная частота системы, т.е. частота, с которой совершались бы колебания в отсутствии затухания. Выражение коэффициента затухания через параметры системы зависит от вида колебательной системы. Для решения уравнения
- собственная частота системы, т.е. частота, с которой совершались бы колебания в отсутствии затухания. Выражение коэффициента затухания через параметры системы зависит от вида колебательной системы. Для решения уравнения 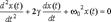 производится подстановка
производится подстановка 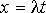 .Эта подстановка приводит к характеристическому уравнению:
.Эта подстановка приводит к характеристическому уравнению: 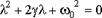 которое имеет два корня:
которое имеет два корня: 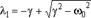
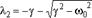
При не слишком большом затухании (при 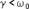 ) подкоренное выражение будет отрицательным. Если его представить в виде
) подкоренное выражение будет отрицательным. Если его представить в виде 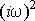 где
где 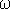 - вещественная положительная величина, называемая циклической частотой затухающих колебаний и равная
- вещественная положительная величина, называемая циклической частотой затухающих колебаний и равная 
то корни уравнения запишутся в виде: 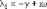
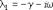 Общим решением уравнения будет функция:
Общим решением уравнения будет функция: 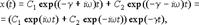 которую можно представить в виде:
которую можно представить в виде: 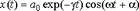 Здесь
Здесь 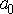 и
и 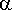 - произвольные постоянные.движение системы можно условно рассматривать как гармоническое колебание частоты w с амплитудой, изменяющейся по закону:
- произвольные постоянные.движение системы можно условно рассматривать как гармоническое колебание частоты w с амплитудой, изменяющейся по закону: 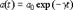 Период затухающих колебаний определяется формулой:
Период затухающих колебаний определяется формулой: 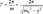 При незначительном затухании период колебаний практически равен
При незначительном затухании период колебаний практически равен 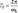
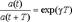 Такое отношение амплитуд называется декрементом затухания, а его натуральный логарифм - логарифмическим декрементом затухания:
Такое отношение амплитуд называется декрементом затухания, а его натуральный логарифм - логарифмическим декрементом затухания: 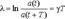 Логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в «e» раз. Помимо рассмотренных величин для характеристики колебательной системы употребляется величина
Логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в «e» раз. Помимо рассмотренных величин для характеристики колебательной системы употребляется величина 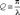 называемаядобротностью колебательной системы. Добротность пропорциональна числу колебаний, совершаемых системой за то время, за которое амплитуда колебаний уменьшается в «e» раз.время релаксации — время, за которое амплитуда колебаний уменьшится в e раз.
называемаядобротностью колебательной системы. Добротность пропорциональна числу колебаний, совершаемых системой за то время, за которое амплитуда колебаний уменьшается в «e» раз.время релаксации — время, за которое амплитуда колебаний уменьшится в e раз.
49. Электрический заряд. Закон Кулона. Электростатическое поле (ЭСП). Напряженность ЭСП. Принцип суперпозиции. Силовые линии ЭСП.Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия. Электрический заряд обычно обозначается буквами q или Q. Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:Существует два рода электрических зарядов, условно названных положительными и отрицательными.Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.закон сохранения электрического заряда-в изолированной системе алгебраическая сумма зарядов всех тел остается постоянной q1 + q2 + q3 + ... +qn = const. Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному заряду e. e = 1,6·10–19 Кл. Совокупность двух равных по величине разноименных точечных зарядов q, расположенных на некотором расстоянии 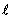 друг от друга, малом по сравнению с расстоянием до рассматриваемой точки поля называется электрическим диполем.(рис.13.1)
друг от друга, малом по сравнению с расстоянием до рассматриваемой точки поля называется электрическим диполем.(рис.13.1)  Закон Кулона: Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
Закон Кулона: Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними: 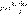 коэффициент к записывается в си:
коэффициент к записывается в си: 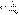 ЭЛЕКТРОСТАТИ́ЧЕСКОЕ ПО́ЛЕ, электрическое поле неподвижных и не меняющихся со временем электрических зарядов, осуществляющее взаимодействие между ними. Электростатическое поле характеризуется напряженностью электрического поля Е, которая является его силовой характеристикой: Напряженность электростатического поля показывает, с какой силой электростатическое поле действует на единичный положительный электрический заряд, помещенный в данную точку поля
ЭЛЕКТРОСТАТИ́ЧЕСКОЕ ПО́ЛЕ, электрическое поле неподвижных и не меняющихся со временем электрических зарядов, осуществляющее взаимодействие между ними. Электростатическое поле характеризуется напряженностью электрического поля Е, которая является его силовой характеристикой: Напряженность электростатического поля показывает, с какой силой электростатическое поле действует на единичный положительный электрический заряд, помещенный в данную точку поля
Электростатическое поле однородно, если вектор его напряженности одинаков во всех точках поля, если вектор напряженности в различных точках различается, поле неоднородно. То есть электростатическое поле - это потенциальное поле, энергетической характеристикой которого является электростатический потенциал , связанным с вектором напряженности Е соотношением
Е = -gradj.Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, которая действует на пробный единичный положительный заряд, помещенный в эту точку поля: 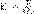 (1) Как следует из формулы (1) и закона Кулона, напряженность поля точечного заряда в вакууме
(1) Как следует из формулы (1) и закона Кулона, напряженность поля точечного заряда в вакууме 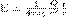 или
или 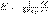 (2) Направление вектора Е совпадает с направлением силы, которая действует на положительный заряд. Если поле создается положительным зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положительного заряда); если поле создается отрицательным зарядом, то вектор Е направлен к заряду. За единицу напряженности принимается напряженность в такой точке поля, в которой на единицу заряда действует единица силы.
(2) Направление вектора Е совпадает с направлением силы, которая действует на положительный заряд. Если поле создается положительным зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положительного заряда); если поле создается отрицательным зарядом, то вектор Е направлен к заряду. За единицу напряженности принимается напряженность в такой точке поля, в которой на единицу заряда действует единица силы. 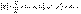
Принцип суперпозиции- результат воздействия на частицу нескольких внешних сил есть просто сумма результатов воздействия каждой из сил. Силовые линии электрического и магнитного полей, линии, касательные к которым в каждой точке поля совпадают с направлением напряжённости электрического или соответственно магнитного поля; качественно характеризуют распределение электромагнитного поля в пространстве. Силовые линии — только наглядный способ изображения силовых полей 
 Силовые линии электростатического поля всегда незамкнуты: они начинаются на положительных зарядах и оканчиваются на отрицательных (или уходят на бесконечность). Силовые линии нигде не пересекаются, так как в каждой точке поля его напряженность имеет одно единственное значение и определенное направление. Густота силовых линий больше вблизи заряженных тел, где напряженность поля больше.
Силовые линии электростатического поля всегда незамкнуты: они начинаются на положительных зарядах и оканчиваются на отрицательных (или уходят на бесконечность). Силовые линии нигде не пересекаются, так как в каждой точке поля его напряженность имеет одно единственное значение и определенное направление. Густота силовых линий больше вблизи заряженных тел, где напряженность поля больше.
Силовые линии электрического поля в пространстве между двумя положительными зарядами расходятся; можно указать нейтральную точку, в которой поля сил отталкивания обоих зарядов гасят друг друга.
50.Работа по перемещению заряда в ЭСП. Потенциальная энергия и заряд ЭСП. Принцип суперпозиции. Теорема о циркуляции для ЭСП.Работу по перемещению заряда в электростатическом поле удобно представить в виде 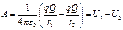 где U1 и U2 представляют собой величину потенциальной энергии в начальной и конечной точках при перемещения заряда в электростатическом поле. Потенциальная энергия и заряд ЭСПОтношение величины потенциальной энергии пробного заряда в рассматриваемой точке электростатического поля к величине этого заряда называется потенциалом электростатического поля и является энергетической характеристикой электрического поля
где U1 и U2 представляют собой величину потенциальной энергии в начальной и конечной точках при перемещения заряда в электростатическом поле. Потенциальная энергия и заряд ЭСПОтношение величины потенциальной энергии пробного заряда в рассматриваемой точке электростатического поля к величине этого заряда называется потенциалом электростатического поля и является энергетической характеристикой электрического поля 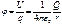 Для системы электрических зарядов
Для системы электрических зарядов 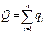 и
и 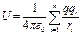 →
→ 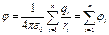 что означает, что потенциалы подчиняются правилу аддитивности. Если заряд распределен в пространстве непрерывно, то
что означает, что потенциалы подчиняются правилу аддитивности. Если заряд распределен в пространстве непрерывно, то 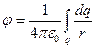 Принцип суперпозиции- результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил. Теорема о циркуляции для ЭСПЕсли в качестве перемещаемого заряда выбрать единичный точечный заряд, то работу сил поля можно выразить через напряженность Е
Принцип суперпозиции- результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил. Теорема о циркуляции для ЭСПЕсли в качестве перемещаемого заряда выбрать единичный точечный заряд, то работу сил поля можно выразить через напряженность Е 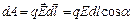 Тогда при перемещении единичного точечного заряда по замкнутому контуру получим
Тогда при перемещении единичного точечного заряда по замкнутому контуру получим 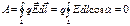 Интеграл
Интеграл 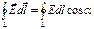 называют циркуляцией вектора напряженности. Поле, у которого циркуляция вектора напряженности вдоль любого замкнутого контура равна нулю, называется потенциальным, а силы создающие это поле – консервативными.
называют циркуляцией вектора напряженности. Поле, у которого циркуляция вектора напряженности вдоль любого замкнутого контура равна нулю, называется потенциальным, а силы создающие это поле – консервативными.
51. Поток вектора напряженности ЭСП. Теорема Гаусса. Применение теоремы Гаусса к расчету ЭСП. Бесконечной равномерно заряженной плоскости.
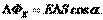 Если поле неоднородно или поверхность, через которую вычисляется поток, не является плоской
Если поле неоднородно или поверхность, через которую вычисляется поток, не является плоской 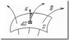 , то определение потока нужно применить к бесконечно малому элементу поверхности, а именно записать:
, то определение потока нужно применить к бесконечно малому элементу поверхности, а именно записать: 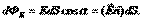 Тогда поток через всю поверхность S будет:
Тогда поток через всю поверхность S будет: 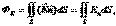 ,где
,где 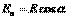 . Теорема Гаусса — один из основных законов электродинамики. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью.Применение теоремы Гаусса к расчету ЭСП.Объёмная плотность заряда
. Теорема Гаусса — один из основных законов электродинамики. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью.Применение теоремы Гаусса к расчету ЭСП.Объёмная плотность заряда 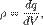 где dV — (бесконечно малый) элемент объема, Поверхностная плотность заряда
где dV — (бесконечно малый) элемент объема, Поверхностная плотность заряда 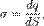 где dS — (бесконечно малый) элемент поверхности. Линейная плотность заряда
где dS — (бесконечно малый) элемент поверхности. Линейная плотность заряда 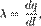 где dl — длина бесконечно малого отрезка. (Первая используется для зарядов, непрерывно распределенных по объему, вторая — для распределенных по поверхности, третья — для распределенных по одномерной линии (кривой, прямой).искомая напряженность электрического поля равномерно заряженной плоскости.
где dl — длина бесконечно малого отрезка. (Первая используется для зарядов, непрерывно распределенных по объему, вторая — для распределенных по поверхности, третья — для распределенных по одномерной линии (кривой, прямой).искомая напряженность электрического поля равномерно заряженной плоскости. 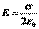 Применив теорему Гаусса, и учитывая Q = σΔS, получим (в системе СИ):
Применив теорему Гаусса, и учитывая Q = σΔS, получим (в системе СИ): 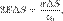 из чего
из чего 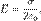 Поток вектора напряжённости равен (в силу (1)) потоку только через основания цилиндра, а он, в силу того, что E' и E'' перпендикулярны этим основаниям и в силу (2), равен просто 2EΔS.
Поток вектора напряжённости равен (в силу (1)) потоку только через основания цилиндра, а он, в силу того, что E' и E'' перпендикулярны этим основаниям и в силу (2), равен просто 2EΔS.
52.Поток вектора напряженности ЭСП. Теорема Гаусса. Применение теоремы Гаусса к расчету ЭСП. Бесконечной равномернозаряженной нити. 
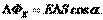 Если поле неоднородно или поверхность, через которую вычисляется поток, не является плоской
Если поле неоднородно или поверхность, через которую вычисляется поток, не является плоской
Поле равномерно заряженной нити (цилиндра).  то определение потока нужно применить к бесконечно малому элементу поверхности, а именно записать:
то определение потока нужно применить к бесконечно малому элементу поверхности, а именно записать: 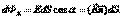 Тогда поток через всю поверхность S будет:
Тогда поток через всю поверхность S будет: 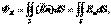 ,где
,где 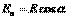 . Теорема Гаусса — один из основных законов электродинамики. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью.
. Теорема Гаусса — один из основных законов электродинамики. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. 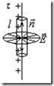 В данном случае электрическое поле обладает аксиальной симметрией – не зависит от азимутального угла φ и координаты z и направлено вдоль радиус-вектора
В данном случае электрическое поле обладает аксиальной симметрией – не зависит от азимутального угла φ и координаты z и направлено вдоль радиус-вектора  (рис.2.6). Поэтому для потока вектора E через выбранную цилиндрическую поверхность с осью, совпадающей с заряженной нитью, имеем:
(рис.2.6). Поэтому для потока вектора E через выбранную цилиндрическую поверхность с осью, совпадающей с заряженной нитью, имеем: 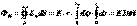 , где
, где 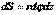 - элемент цилиндрической поверхности; l – длина произвольного участка нити.С другой стороны, по теореме Гаусса этот поток равен:
- элемент цилиндрической поверхности; l – длина произвольного участка нити.С другой стороны, по теореме Гаусса этот поток равен: 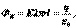 причем
причем 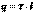 ,
,  - линейная плотность заряда нити. Поле равномерно заряженной нити.Отсюда находим:
- линейная плотность заряда нити. Поле равномерно заряженной нити.Отсюда находим: 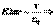
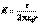 .Искомая напряженность электрического поля равномерно заряженной нити:
.Искомая напряженность электрического поля равномерно заряженной нити: 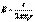
53.Эквипотенциальные поверхности. Связь напряженности и потенциала. ЭКВИПОТЕНЦИА́ЛЬНАЯ ПОВЕ́РХНОСТЬ, поверхность, во всех точках которой потенциал электрического поля имеет одинаковое значение j= const. На плоскости эти поверхности представляют собой эквипотенциальные линии поля. Используются для графического изображения распределения потенциала. Эквипотенциальные поверхности замкнуты и не пересекаются. Изображение эквипотенциальных поверхностей осуществляют таким образом, чтобы разности потенциалов между соседними эквипотенциальными поверхностями были одинаковы. В этом случае в тех участках, где линии эквипотенциальных поверхностей расположены гуще, больше напряженность поля. Эквипотенциальными поверхностями поля точечного электрического заряда являются сферы, в центре которых расположен заряд. Эквипотенциальные поверхности однородного электрического поля представляют собой плоскости, перпендикулярные линиям напряженности. Поверхность проводника в электростатическом поле является эквипотенциальной поверхностью.Электрическое поле характеризуется двумя физическими величинами: напряженностью (силовая характеристика) и потенциалом (энергетическая характеристика). Выясним как они связаны между собой. Пусть положительный заряд q перемещается силой электрического поля с эквипотенциальной поверхности, имеющей потенциал фи0, на близко расположенную эквипотенциальную поверхность, имеющую потенциал 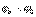
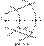 Напряженность поля Е на всем малом пути dx можно считать постоянной. Тогда работа перемещения
Напряженность поля Е на всем малом пути dx можно считать постоянной. Тогда работа перемещения 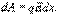 С другой стороны
С другой стороны 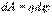 . Из этих уравнений получаем
. Из этих уравнений получаем 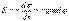 Знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала.
Знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала.
54. Диэлектрики. Связанные и сторонние заряды. Полярные и неполярные молекулы. Поляризация диэлектрика. Вектор поляризованности. Диэлектрические проницаемость и восприимчивость. Диэлектрики, вещества, плохо проводящие электрический ток. Состоит из молекул(атомов).3типа диэлектриков: неполярные-диэл. с неполярными молекулам(H2,O2).Полярные диэл они с полярными молекулами(вода,спирт). Ионные диэл имеют ионную кристаллическую решётку. Связанные заряды-нескампенсированные заряды,которые появились в результате поляризации на поверхности диэлектрика в электрическом поле.Они не могут передвигаться свободно и перемещаться только внутри молекул. Сторонниезаряды-первичные источники электрического поля в диэлектрике, E=E0+Eштрих (E-вектор)Е0вектор и Ештрих вектор – это макрополя. ПОЛЯРНЫЕ МОЛЕКУЛЫ, молекулы, обладающие постоянным дипольным моментом в отсутствие внеш. электрич. поля. Дипольный момент присущ таким молекулам, у к-рых распределение электронного и ядерного зарядов не имеет центра симметрии. чем больше дипольный момент, тем сильнее полярность В-ва, образованные сильно полярными молекулами как правило, хорошо раств. В случае неполярных молекул происходит смещение в пределах молекул их положительных зарядов в направлении внешнего поля и отрицательных в противоположном направлении. Для вещества, состоящего из полярных молекул, под действием момента сил происходит преимущественное выстраивание молекул в направлении внешнего поля. В обоих случаях (неполярных и полярных молекул) в результате появляется дипольный момент и у всего объема диэлектрика.Поляризацией диэлектрика называется процесс, в результате которого физический обьект(атом,молекула,ТВ.тело идр.)приобретает электрический дипольный момент. Степень поляризации диэлектрика характеризуется векторной величиной, которая называется поляризованостью или вектором поляризации(P). Поляризованность определяется как электрический момент единицы объема диэлектрика 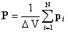 где N - число молекул в объеме
где N - число молекул в объеме 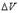 . Поляризованность P часто называют поляризацией, понимая под этим количественную меру этого процесса. ДИЭЛЕКТРИ́ЧЕСКАЯ ПРОНИЦА́ЕМОСТЬ, безразмерная величина e, показывающая, во сколько раз сила взаимодействия F между электрическими зарядами в данной среде меньше их силы взаимодействия Fo в вакууме: e =Fо/F. Диэлектрическая проницаемость показывает, во сколько раз поле ослабляется диэлектриком. Диэлектри́ческая восприи́мчивость (или поляризу́емость) вещества — физическая величина, мера способности вещества поляризоваться под действием электрического поля. Диэлектрическая восприимчивость χe — коэффициент линейной связи между поляризацией диэлектрика P и внешним электрическим полем E в достаточно малых полях:
. Поляризованность P часто называют поляризацией, понимая под этим количественную меру этого процесса. ДИЭЛЕКТРИ́ЧЕСКАЯ ПРОНИЦА́ЕМОСТЬ, безразмерная величина e, показывающая, во сколько раз сила взаимодействия F между электрическими зарядами в данной среде меньше их силы взаимодействия Fo в вакууме: e =Fо/F. Диэлектрическая проницаемость показывает, во сколько раз поле ослабляется диэлектриком. Диэлектри́ческая восприи́мчивость (или поляризу́емость) вещества — физическая величина, мера способности вещества поляризоваться под действием электрического поля. Диэлектрическая восприимчивость χe — коэффициент линейной связи между поляризацией диэлектрика P и внешним электрическим полем E в достаточно малых полях: 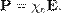
55. Теорема Гаусса для диэлектриков. Вектор электрического смещения. В диэлектрике теорема Гаусса справедлива для потока вектора электрической индукции D:
div D = 4*(пи)*g , где g - суммарный свободный заряд внутри поверхности S. Если электрическое поле имеет место в диэлектрике, то наблюдается поляризация вещества и появляются связанные электрические заряды. Учитывают поляризацию с помощью ектора поляризации 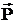 , который для анизотропных и однородных сред выражается через напряженность поля следующим образом:
, который для анизотропных и однородных сред выражается через напряженность поля следующим образом: 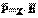 , где c – диэлектрическая восприимчивость вещества (диэлектрика). Вектор поляризации равен также поверхностной плотности связанных зарядов, возникающих в диэлектрике под воздействием внешнего электрического поля (Р = sсвяз ).Кроме этого, при анализе электростатических полей используют вектор электрического смещения
, где c – диэлектрическая восприимчивость вещества (диэлектрика). Вектор поляризации равен также поверхностной плотности связанных зарядов, возникающих в диэлектрике под воздействием внешнего электрического поля (Р = sсвяз ).Кроме этого, при анализе электростатических полей используют вектор электрического смещения 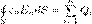 Единицей электрического смещения является кулон на метр квадратный (Кл/м2).Величина e = e0 + c является основной характеристикой диэлектрика и называется абсолютной диэлектрической проницаемостью. Отношение er = e/e0 называют относительной диэлектрической проницаемостью.
Единицей электрического смещения является кулон на метр квадратный (Кл/м2).Величина e = e0 + c является основной характеристикой диэлектрика и называется абсолютной диэлектрической проницаемостью. Отношение er = e/e0 называют относительной диэлектрической проницаемостью.
56. Проводники в ЭСП. Индукционные заряды. Напряженность и потенциал внутри и вблизи поверхности проводника. Электростатическая защита. Проводники - это вещества, в которых есть свободные заряды. Свободные заряды - заряды частиц, которые могут перемещаться внутри проводника (под действием электрического поля). К проводникам относятся в первую очередь металлы, в которых носителями свободных зарядов являются электроны. Электростатического поля внутри проводника нет. Если бы оно там было, свободные зарядыдвигались бы под действием кулоновских сил упорядоченно, чего в реальности не происходит. Внутри проводника напряжённость поля равна нулю, то поток напряжённости через любую замкнутую поверхность внутри него равен нулю. Значит, равен нулю заряд внутри любой замкнутой поверхности внутри проводника. Отсюда следует, что, так как внутри проводника заряда нет, то весь его заряд сосредоточен на поверхности. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды – индукционными зарядами. Индукционные заряды создают свое собственное поле 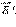 которое компенсирует внешнее поле
которое компенсирует внешнее поле 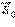 во всем объеме проводника:
во всем объеме проводника: 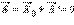 (внутри проводника). Полное электростатическое поле внутри проводника равно нулю, а потенциалы во всех точках одинаковы и равны потенциалу на поверхности проводника. Рассмотрим какую-либо заряженную поверхность произвольной формы с поверхностной плотностью заряда разделяющую два полупространства в которых есть электростатическое поле Возьмем бесконечно малую площадку dS и построим цилиндр очень малой высоты (консервную банку). Тогда по теореме Гаусса (поток через боковую поверхность пренебрежимо мал) имеем
(внутри проводника). Полное электростатическое поле внутри проводника равно нулю, а потенциалы во всех точках одинаковы и равны потенциалу на поверхности проводника. Рассмотрим какую-либо заряженную поверхность произвольной формы с поверхностной плотностью заряда разделяющую два полупространства в которых есть электростатическое поле Возьмем бесконечно малую площадку dS и построим цилиндр очень малой высоты (консервную банку). Тогда по теореме Гаусса (поток через боковую поверхность пренебрежимо мал) имеем 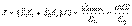 В проекциях на единую нормаль
В проекциях на единую нормаль 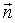 , проведенную от первой области ко второй
, проведенную от первой области ко второй 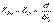 Электростатическаязащита - защита приборов и оборудования, основанная на том, что напряженность электростатического поля внутри проводника равна нулю. Заряд статического электричества возникает на поверхности материалов (особенно диэлектриков) в езультате контакта этих материалов посредством трения, отделения или соединения поверхностей, деформаций, разрыва и т. п.Основной причиной возникновения заряда на поверхности материалов при указанном контакте их является образование так называемого двойного слоя, т. е. образование положительных и отрицательных зарядов, расположенных друг против друга, на соприкасающихся поверхностях в виде противоположно заряженных слоев.
Электростатическаязащита - защита приборов и оборудования, основанная на том, что напряженность электростатического поля внутри проводника равна нулю. Заряд статического электричества возникает на поверхности материалов (особенно диэлектриков) в езультате контакта этих материалов посредством трения, отделения или соединения поверхностей, деформаций, разрыва и т. п.Основной причиной возникновения заряда на поверхности материалов при указанном контакте их является образование так называемого двойного слоя, т. е. образование положительных и отрицательных зарядов, расположенных друг против друга, на соприкасающихся поверхностях в виде противоположно заряженных слоев.
57.Электроемкость уединенного проводника. Конденсаторы. Емкость плоского конденсатора. Соединения конденсаторов.Электроемкость уединенного проводника - это физическая величина, численно равная заряду, необходимoму для повышения потенциала проводника на 1 В. Электрический конденсатор представляет собой систему из двух проводников электрического тока (обкладок), разделенных диэлектриком. Основной характеристикой конденсатора является его электрическая емкость, или просто емкость, которая характеризует способность конденсатора накапливать электрический заряд. Емкость конденсатора определяется отношением накапливаемого на одной из обкладок электрического заряда к приложенному напряжению: С=q/U. Она зависит от материала диэлектрика, формы и взаимного расположения обкладок.В цепях постоянного тока конденсатор не проводит электрический ток, поскольку между его обкладками находится диэлектрик.Электроемкость плоского конденсатора. Плоский конденсатор представляет из себя две плоские пластины, расстояние между которыми d мало по сравнению с их линейными размерами. Это предположение позволяет пренебречь малыми областями неоднородности электрического поля у краев пластин и считать, что все поле однородно и сосредоточено между пластинами. Заряд конденсатора Q - это заряд положительно заряженной пластины.Емкость конденсатора определяется как величина, численно равная заряду, необходимому для изменения разности потенциалов пластин, напряжения U между обкладками, на 1 В:  Заполнение пространства между пластинами диэлектриком, очевидно, увеличит емкость в
Заполнение пространства между пластинами диэлектриком, очевидно, увеличит емкость в  раз. У конденсаторов существует два вида соединения: последовательное и параллельное. Последовательное соединение. В этом случае обкладка одного конденсатора, заряженная отрицательно, соединена с обкладкой другого конденсатора, заряженного положительно. На рисунке показан пример последовательного соединения конденсаторов.
раз. У конденсаторов существует два вида соединения: последовательное и параллельное. Последовательное соединение. В этом случае обкладка одного конденсатора, заряженная отрицательно, соединена с обкладкой другого конденсатора, заряженного положительно. На рисунке показан пример последовательного соединения конденсаторов. 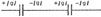
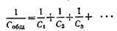 Параллельное соединение. При параллельном соединении конденсаторов положительно заряженные обкладки соединены с положительно заряженными, а отрицательно заряженные — с отрицательными.
Параллельное соединение. При параллельном соединении конденсаторов положительно заряженные обкладки соединены с положительно заряженными, а отрицательно заряженные — с отрицательными.  Собщ = С1 + С2 + С3
Собщ = С1 + С2 + С3
58.Энергия системы точечных зарядов. Энергия заряженного конденсатора. Энергия ЭСП. Плотность энергии. используем формулу потенциала уединенного заряда 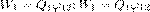 где φ12 и φ21 — соответственно потенциалы, которые создаются зарядом Q2 в точке нахождения заряда Q1 и зарядом Q1 в точке нахождения заряда Q2. Согласно,
где φ12 и φ21 — соответственно потенциалы, которые создаются зарядом Q2 в точке нахождения заряда Q1 и зарядом Q1 в точке нахождения заряда Q2. Согласно, 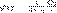
поэтому W1 = W2 = W и W=Q1фи12=Q2фи21=(1/2)(Q1фи12+Q2фи21)
Добавляя к нашей системе из двух зарядов последовательно заряды Q3, Q4, ... , можно доказать, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна 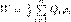 где φi — потенциал, который создается в точке, где находится заряд Qi, всеми зарядами, кроме i-го.Энергия заряженного конденсатора. Конденсатор состоит из заряженных проводников поэтому обладает энергией, которая из формулы
где φi — потенциал, который создается в точке, где находится заряд Qi, всеми зарядами, кроме i-го.Энергия заряженного конденсатора. Конденсатор состоит из заряженных проводников поэтому обладает энергией, которая из формулы  равна
равна 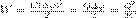 где Q — заряд конденсатора, С — его емкость, Δφ — разность потенциалов между обкладками конденсатора.Энергия электростатического поля. Используем выражение (4), которое выражает энергию плоского конденсатора посредством зарядов и потенциалов, и спользуя выражением для емкости плоского конденсатора (C=ε0εS/d) и разности потенциалов между его обкладками (Δφ=Ed. Тогда
где Q — заряд конденсатора, С — его емкость, Δφ — разность потенциалов между обкладками конденсатора.Энергия электростатического поля. Используем выражение (4), которое выражает энергию плоского конденсатора посредством зарядов и потенциалов, и спользуя выражением для емкости плоского конденсатора (C=ε0εS/d) и разности потенциалов между его обкладками (Δφ=Ed. Тогда 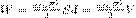 где V= Sd — объем конденсатора. Формула говорит о том, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, — напряженность Е.Плотность энергии — количество энергии на единицу объёма.
где V= Sd — объем конденсатора. Формула говорит о том, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, — напряженность Е.Плотность энергии — количество энергии на единицу объёма. 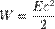 -это плотность энергии упругого тела, где ε — относительная деформация, E — модуль Юнга
-это плотность энергии упругого тела, где ε — относительная деформация, E — модуль Юнга
59. Электрический ток в проводниках. Характеристики электрического тока. Источник тока. ЭДС. Однородный и неоднородный участки цепи.электрическим током называется упорядоченное движение заряженных частиц. Чтобы электрический ток в проводнике существовал длительное время, необходимо все это время поддерживать в нем электрическое поле. Электрическое поле в проводниках создается и может длительное время поддерживаться источниками электрического тока. В настоящее время человечество использует четыре основные источника тока: статический, химический, механический и полупроводниковый, но во всяком из них совершается работа по разделению положительно и отрицательно заряженных частиц. Раздельные частицы накапливаются на полюсах источника тока. Один полюс источника тока заряжается положительно, другой - отрицательно.Электрический ток в проводниках представляет собой: в металлах — направленное движение электронов (проводники первого рода); в электролитах — направленное движение положительных и отрицательных ионов; в плазме — направленное движение электронов и ионов обоих знаков За направление электрического тока условились считать направление движения положительно заряженных частиц. Сила тока — скалярная физическая величина, равная отношением заряда Δq, проходящего через поперечное сечение проводника за некоторый промежуток времени Δt, к этому промежутку: 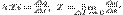 Плотность тока j — это векторная физическая величина, модуль которой равен отношению силы тока I в проводнике к площади S поперечного сечения проводника:
Плотность тока j — это векторная физическая величина, модуль которой равен отношению силы тока I в проводнике к площади S поперечного сечения проводника: 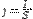 источник тока - это элемент электрической цепи, поддерживающий в этой цепи ток заданного значения, не зависящего от сопротивления прочих элементов цепи. Электродвижущая сила (эдс), физическая величина, характеризующая действие сторонних (непотенциальных) сил в источниках постоянного или переменного тока; в замкнутом проводящем контуре равна работе этих сил по перемещению единичного положительного заряда вдоль контура. Если через Eстр обозначить напряжённость поля сторонних сил, то эдс в замкнутом контуре (L) равна
источник тока - это элемент электрической цепи, поддерживающий в этой цепи ток заданного значения, не зависящего от сопротивления прочих элементов цепи. Электродвижущая сила (эдс), физическая величина, характеризующая действие сторонних (непотенциальных) сил в источниках постоянного или переменного тока; в замкнутом проводящем контуре равна работе этих сил по перемещению единичного положительного заряда вдоль контура. Если через Eстр обозначить напряжённость поля сторонних сил, то эдс в замкнутом контуре (L) равна 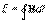 , где dl — элемент длины контура. Однородный и неоднородный участки цепи. Поле, в каждой точке которого вектор напряженности остается постоянным по величине и направлению, называется однородным. В противном случае поле называется неоднородным. Поля точечных зарядов - неоднородные поля..Закон Ома для однородного участка цепи. Сила тока в участке цепи прямо пропорциональна напряжению на нем и обратно пропорциональна сопротивлению участка I = U / R. Закон Ома для неоднородного участка цепи- Сила тока в неоднородном участке цепи прямо пропорциональна сумме разности потенциалов на его концах и действующей в нем ЭДС и обратно пропорциональна сопротивлению участка: I = (φ1 − φ2 + ε) / (R + r), где R - сопротивление внешнего участка цепи, r - внутреннее сопротивление.
, где dl — элемент длины контура. Однородный и неоднородный участки цепи. Поле, в каждой точке которого вектор напряженности остается постоянным по величине и направлению, называется однородным. В противном случае поле называется неоднородным. Поля точечных зарядов - неоднородные поля..Закон Ома для однородного участка цепи. Сила тока в участке цепи прямо пропорциональна напряжению на нем и обратно пропорциональна сопротивлению участка I = U / R. Закон Ома для неоднородного участка цепи- Сила тока в неоднородном участке цепи прямо пропорциональна сумме разности потенциалов на его концах и действующей в нем ЭДС и обратно пропорциональна сопротивлению участка: I = (φ1 − φ2 + ε) / (R + r), где R - сопротивление внешнего участка цепи, r - внутреннее сопротивление.
60. Законы Ома и Джоуля-Ленца в дифференциальной и интегральной формах.Закон Ома для однородного участка цепи. Сила тока в участке цепи прямо пропорциональна напряжению на нем и обратно пропорциональна сопротивлению участка I = U / R. Закон Ома для неоднородного участка цепи- Сила тока в неоднородном участке цепи прямо пропорциональна сумме разности потенциалов на его концах и действующей в нем ЭДС и обратно пропорциональна сопротивлению участка: I = (φ1 − φ2 + ε) / (R + r), где R - сопротивление внешнего участка цепи, r - внутреннее сопротивление..Закон Ома для полной цепиСила тока в цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна сумме сопротивлений внешнего и внутреннего участков цепи: I = ε / (R + r).Закон Джоуля-Ленца. Количество теплоты, выделившейся в проводнике при прохождении по нему электрического тока, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока:Q = I2 R t.Если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. Опыт показывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов 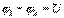 , тогда работу по переносу заряда q на этом участке равна
, тогда работу по переносу заряда q на этом участке равна 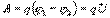 По определению I= q/t. откуда q= I t. Следовательно
По определению I= q/t. откуда q= I t. Следовательно 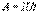 Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил
Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил 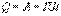 ЭТО Соотношение выражает закон Джоуля-Ленца в интегральной форме. Введем плотность тепловой мощности
ЭТО Соотношение выражает закон Джоуля-Ленца в интегральной форме. Введем плотность тепловой мощности 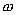 , равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника
, равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника 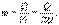 где S - поперечное сечение проводника, l- его длина. Используя и соотношение
где S - поперечное сечение проводника, l- его длина. Используя и соотношение 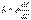 , получим
, получим 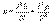 Но
Но 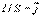 - плотность тока, а
- плотность тока, а 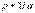 , тогда
, тогда 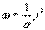 с учетом закона Ома в дифференциальной форме
с учетом закона Ома в дифференциальной форме 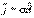 , окончательно получаем
, окончательно получаем 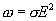 Формула выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.
Формула выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.
61. Соединение сопротивлений в ЭДС. Правила Кирхгофа. Основной характеристики источника является электродвижущая сила [1] (ЭДС) – работа, совершаемая сторонними силами по перемещению единичного положительного заряда 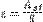 Суммарная работа электростатических и сторонних сил по перемещению единичного положительного заряда называется электрическим напряжением на участке цепи
Суммарная работа электростатических и сторонних сил по перемещению единичного положительного заряда называется электрическим напряжением на участке цепи 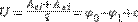 когда сторонние силы отсутствуют, электрическое напряжение совпадает с разностью потенциалов электрического поля.
когда сторонние силы отсутствуют, электрическое напряжение совпадает с разностью потенциалов электрического поля.  чевидно, что работа по преодолению этих сил не зависит от направления движения, так как силы сопротивления всегда направлены в сторону, противоположную скорости движения частиц. Так как силы сопротивления пропорциональны средней скорости движения частиц, то работа по их преодолению пропорциональна скорости движения, следовательно, силе тока силе. Таким образом, мы можем ввести еще характеристику источника – его внутренне сопротивление r, аналогично обычному электрическому сопротивлению. Работа по преодолению сил сопротивления при перемещении единичного положительного заряда между полюсами источника равна
чевидно, что работа по преодолению этих сил не зависит от направления движения, так как силы сопротивления всегда направлены в сторону, противоположную скорости движения частиц. Так как силы сопротивления пропорциональны средней скорости движения частиц, то работа по их преодолению пропорциональна скорости движения, следовательно, силе тока силе. Таким образом, мы можем ввести еще характеристику источника – его внутренне сопротивление r, аналогично обычному электрическому сопротивлению. Работа по преодолению сил сопротивления при перемещении единичного положительного заряда между полюсами источника равна 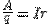 . Еще раз подчеркнем, эта работа не зависит от направления тока в источнике.Правила КирхгофаПравило вытекает из закона сохранения заряда и состоит в том, что алгебраическая сумма сил токов lk, сходящихся в любой точке разветвления проводников (узле), равна нулю, т. е.
. Еще раз подчеркнем, эта работа не зависит от направления тока в источнике.Правила КирхгофаПравило вытекает из закона сохранения заряда и состоит в том, что алгебраическая сумма сил токов lk, сходящихся в любой точке разветвления проводников (узле), равна нулю, т. е. 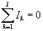 l — число токов, сходящихся в данном узле, причём токи, притекающие к узлу, считаются положительными, а токи, вытекающие из него,— отрицательными. Второе К. и. в любом замкнутом контуре, произвольно выделенном в сложной сети проводников алгебраическая сумма всех падений напряжений lkRk на отд. участках контура равна алгебраической сумме электродвижущих сил (эдс) Ek в этом контуре, т. е.
l — число токов, сходящихся в данном узле, причём токи, притекающие к узлу, считаются положительными, а токи, вытекающие из него,— отрицательными. Второе К. и. в любом замкнутом контуре, произвольно выделенном в сложной сети проводников алгебраическая сумма всех падений напряжений lkRk на отд. участках контура равна алгебраической сумме электродвижущих сил (эдс) Ek в этом контуре, т. е. 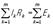 здесь m — число участков в замкнутом контуре), Ik и Rk — сила тока и сопротивление участка номера k; при этом следует выбрать положительное направление токов и эдс, например, считать их положительными, если направление тока совпадает с направлением обхода контура по часовой стрелке, а ЭДС повышает потенциал в направлении этого обхода, и отрицательными — при противоположном направлении
здесь m — число участков в замкнутом контуре), Ik и Rk — сила тока и сопротивление участка номера k; при этом следует выбрать положительное направление токов и эдс, например, считать их положительными, если направление тока совпадает с направлением обхода контура по часовой стрелке, а ЭДС повышает потенциал в направлении этого обхода, и отрицательными — при противоположном направлении
