Решение дисперсионного уравнения в случае однородной и изотропной среды с пространственной дисперсией

Мы будем рассматривать среды обладающие центром симметрии, т.е. проводить инверсию относительно точки – это упрощает запись тензора 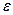. Тензор 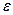может быть разложен на два независимых тензора :

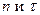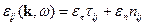
Можно показать, что 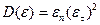. Тогда продольные волны могут существовать при 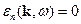. А поперечные волны могут существовать при 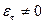и .

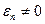Если рассчитать для 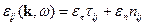выражение 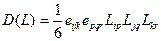, то получается уравнение Френеля:

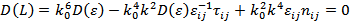
Получаем два корня данного уравнения: 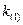и 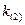, которые мы берём по абсолютному значению, т.е. в кристалле распространяются две поперечные волны.

В случае 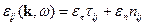решение уравнения 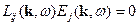может быть упрощено:

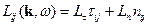
Тогда для поперечной составляющей:

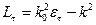
для продольной ( ):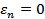

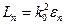
Тогда из

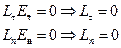
получаем

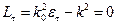
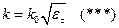
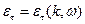
Здесь два одинаковых решения, т.к. среда изотропная.

Уравнение (***) трансцендентное, оно решается методом последовательных приближений. В нулевом приближении можно взять 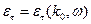.