Вычисление криволинейного интеграла второго рода, его физический смысл
Интегралов.
2. Замена переменной и внесение под знак дифференциала. Примеры.
3. Несколько важных интегралов ( 4 типа).
Интегрирование по частям.
5. Рациональная дробь. Простейшие дроби. Разложение дроби на простейшие.
Интегрирование простейших дробей.
6. Стандартные замены. Примеры интегралов, в которых применяются стандартные замены.
7. Определенный интеграл – определение,геометрический смысл.
8. Интегрируемость функции. Необходимое и достаточное условия интегрируемости.
9. Свойства определенного интеграла – линейность, аддитивность по промежутку, сохранение
знака, интегрирование неравенства, оценка интеграла, теорема о среднем и следствие из нее,
неравенство Коши-Буняковского.
10. Интеграл с переменным верхним пределом. Теорема Барроу. Формула Ньютона – Лейбница.
11. Интегрирование по частям и замена переменных в определенном интеграле.
12. Вычисление длины дуги плоской кривой с помощью определенного интеграла. Случаи пара-
метрического, явного и полярного задания плоской кривой. Длина эллипса, эллиптический
интеграл.
13. Вычисление площади плоской фигуры с помощью определенного интеграла. Площадь
криволинейного сектора в полярных координатах. Площадь криволинейной трапеции в
случае параметрического задания функции.
14. Вычисление объёма тел с помощью определенного интеграла. Объём тела вращения.
Площадь поверхности тела вращения.
15. Схема применения определенного интеграла к задачам физики – два подхода.
16. Теоремы Гульдена.
17. Несобственные интегралы первого рода – определение, геометрическая иллюстрация.
18. Несобственные интегралы второго рода – определение, геометрическая иллюстрация.
19. Признаки сходимости несобственных интегралов. Абсолютная и условная сходимость.
Эталонные интегралы.
20. Гамма-функция, её свойства и график.
21. Нормальная функция распределения, её свойства и график.
22. Криволинейный интеграл первого рода – определение, свойства.
23. Вычисление криволинейного интеграла первого рода, различные случаи. Применение
к вычислению масс, статических моментов и моментов инерции дуг.
24. Криволинейный интеграл второго рода – определении, теорема существования, векторная и
скалярная формы, свойства.
25. Циркуляция вектора в положительном и отрицательном направлении.
Вычисление криволинейного интеграла второго рода, его физический смысл.
27. Числовой ряд, основные определения. Два вопроса теории рядов.
28.Свойства сходящихся рядов, остаток ряда, необходимый признак сходимости.
29. Знакопостоянные и знакопеременные ряды. Положительные ряды, свойства их частичных
сумм.
30. Признаки сходимости положительных рядов – сравнения, предельный, Даламбера, Коши
радикальный, Коши - Маклорена интегральный.
31. Знакопеременные ряды.Абсолютная и условная сходимость. Основное отличие абсолютно
сходящегося ряда от условно сходящегося.Теорема Римана.
32. Лейбницевские ряды. Теорема Лейбница. Теоремы о лейбницевских рядах.
33. Функциональный ряд – определение, точки сходимости и расходимости, область
сходимости.
Отличие суммы функционального ряда от суммы конечного числа функций. Пример.
34. Равномерная сходимость функционального ряда. Геометрическая иллюстрация.
Теоремы о равномерно сходящихся рядах. Признак равномерной сходимости.
35. Нахождение области сходимости.
36. Степенные ряды – определение, интервал и радиус сходимости.
37. Теоремы о степенных рядах.
38. Ряды Тэйлора. Теорема о разложении функции в степенной ряд. Необходимое и достаточное
условие разложимости функции в степенной ряд. Достаточное условие разложимости
функции в степенной ряд. Способы оценки остатка.
39. Разложения основных элементарных функций в ряд Тэйлора и Маклорена -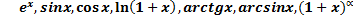 
, прогрессии.
40. Приближенные вычисления с помощью рядов Тэйлора и Маклорена – вычисление значений
функций, вычисление определенных интегралов, аналитическое представление
неэлементарных функций.