Из неравенства (1.1) следует и выполнение неравенства

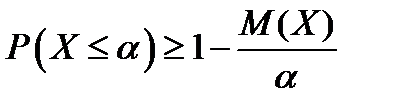(1.2)

Неравенства (1.1) и (1.2) называются неравенствами Маркова.

Пример 1.1. Предположим, что среднее число вызовов, поступающих на телефонную станцию в течение часа, равно 500. Оценить вероятность того, что в течение следующего часа число вызовов превысит 600.

Решение. Пусть случайная величина Х определяет число вызовов в течение часа. Очевидно, что эта величина принимает только неотрицательные значения. По условию М(Х)=500 и α=600. Применяя лемму Маркова, получим 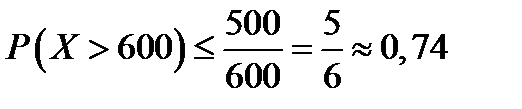, т.е. вероятность того, что число вызовов превысит 600, будет не более 0,74. ■

Рассмотрим теперь случайную величину Х, имеющую математическое ожидание М(Х) и дисперсию D(Х). В следующей лемме Чебышева оценивается вероятность события, состоящего в том, что отклонение Х-М(Х) не превосходит по абсолютной величине положительного числа ε.

Лемма Чебышева.Вероятность того,что отклонение случайной величиныХ от ее математического ожидания по абсолютной величине меньше положительного числа ε, не меньше, чем :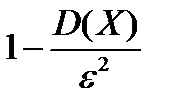

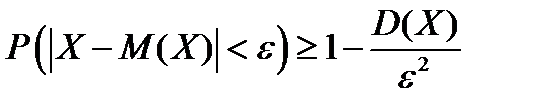. (1.3)

Из неравенства (1.3) следует неравенство

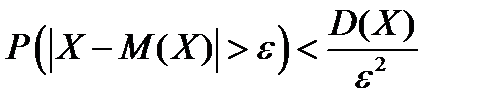(1.4)

Неравенства (1.3) и (1.4) называют неравенствами Чебышева.

Для практики неравенства Чебышева имеют ограниченное значение, так как дают часто грубую, а иногда и совершенно не представляющую интереса оценку. Однако теоретическое значение этих неравенств весьма велико. С их помощью выводится следующая очень важная теорема, составляющая основное содержание закона больших чисел.

Теорема Чебышева.Если Х₁, Х₂, …, Х_n – попарно независимые случайные величины, причем дисперсии их не превышают постоянного числа С, то, как бы мало ни было положительное число ε, вероятность неравенства

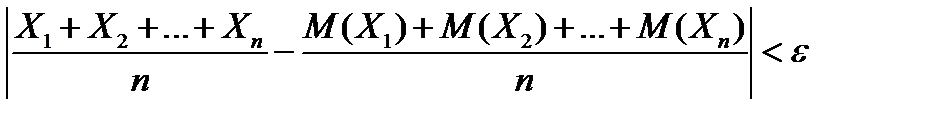
будет как угодно близка к единице, если число случайных величин достаточно велико.

Смысл теоремы Чебышева состоит в том, что при большом числе случайных величин, практически достоверно, что их среднее значение, которое, вообще говоря, является случайной величиной, сколь угодно мало отличается от неслучайной величины (среднего математических ожиданий), т.е. практически перестает быть случайной.

При доказательстве теоремы Чебышева выводится неравенство, которое имеет очень большое значение и иногда формулируется как отдельная теорема.

Следствие 1.В условиях теоремы Чебышева для любого положительного числа ε выполняется неравенство

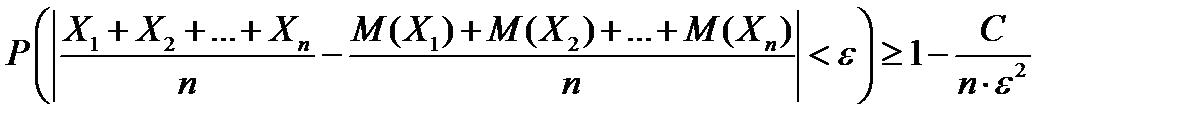(1.5)

В теореме Чебышева предполагалось, что случайные величины могут иметь разные математические ожидания. На практике же часто рассматриваются случайные величины, математические ожидания которых совпадают. В этом случае теорема Чебышева примет вид:

Следствие 2.Если Х₁, Х₂, …, Х_n – попарно независимые случайные величины, имеющие одно и то же математическое ожидание а, причем дисперсии их не превышают постоянного числа С, то, как бы мало ни было положительное число ε, вероятность неравенства

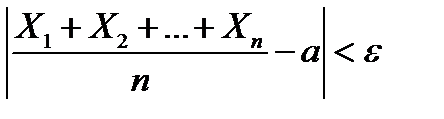
будет как угодно близка к единице, если число случайных величин достаточно велико, или иначе, для любого положительного ε выполняется неравенство

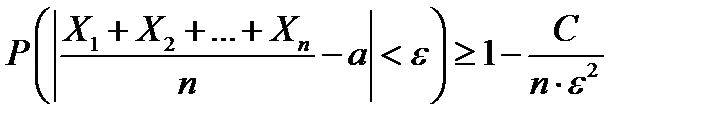(1.6)

Теорема Чебышева имеет большое практическое значение. Именно на этой теореме основан выборочный метод, который является основным методом математической статистики. Теорема позволяет, например, получить представление о величине математического ожидания случайной величины, используя среднее арифметическое некоторых наблюдаемых значений этой величины. Так, измеряя какой-либо параметр с помощью прибора, не дающего систематической погрешности, можно получить достаточно большое число результатов измерений, среднее арифметическое которых будет практически мало отличаться от истинного значения параметра.

Пример 1.2. Найти число измерений некоторой величины, чтобы с вероятностью не менее 0,95 гарантировать отклонение средней арифметической этих измерений от истинного значения величины не более, чем на 1 (по абсолютной величине), если среднеквадратическое отклонение каждого из измерений не превосходит 5?

Решение. Пусть Х_i – результат i-го измерения ( i =1, 2, …, n); а – истинное значение величины, таким образом математическое ожидание Х_i при любом i равно а.

В задаче требуется найти такое n, при котором выполнено неравенство

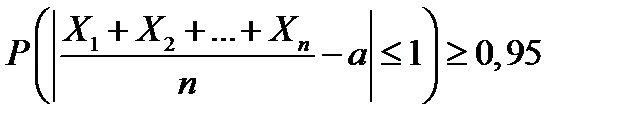
Воспользуемся формулой (1.6).

Имеем 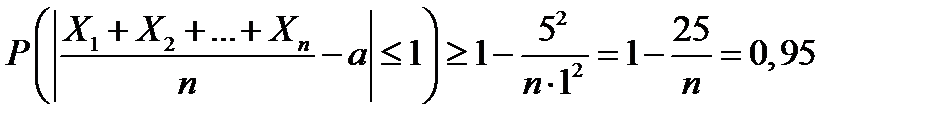. Из последнего равенства находим величину n:

.

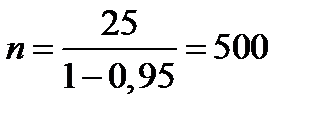Итак, потребуется не менее 500 измерений. ■