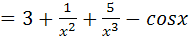Определители и системы линейных уравнений.
При решении системы линейных уравнений с двумя переменными
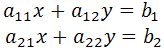Применяя к системе метод уравнивания коэффициентов, получим:
.
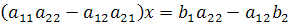
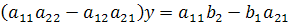Предположим, что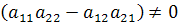 
. Тогда
.
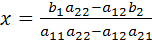
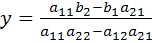Общий знаменатель значений и называется определителем системы уравнений, в данном случае число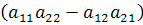 
называется определителем второго порядка и обозначается 
или 
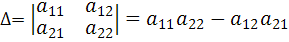
Пример:
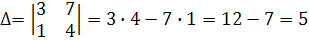
Введение определителей второго порядка не вносит существенных упрощений в решение систем двух линейных уравнений с двумя переменными, и без этого не представляющее никаких затруднений. Аналогичные методы для случая системы трех линейных уравнений с тремя переменными оказываются ужу практически полезными. Пусть дана система линейных уравнений с тремя переменными:
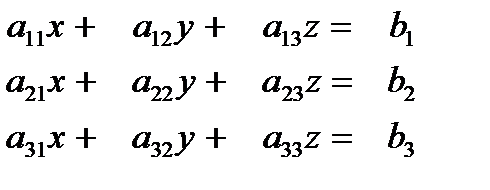
тогда определителем третьего порядка будет выражение: (для его записи употребляется такая же символика, как и в случае определителей второго порядка), таким образом
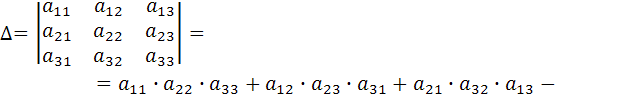
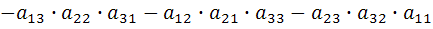
Пример:
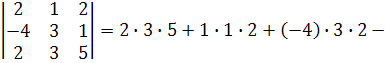
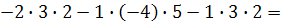30 + 2 - 24- 12 + 20 – 6 = 10
Решение систем линейных уравнений методом Крамера:
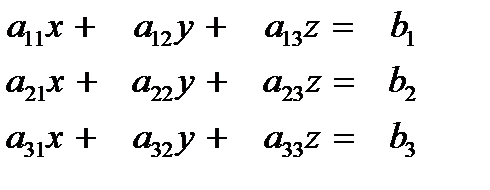
система имеет единственное решение при условии, что определитель системы не равен нулю.
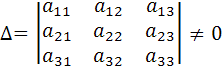
Решение системы находится по формулам:
; 
; 
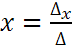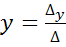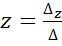. Где
.
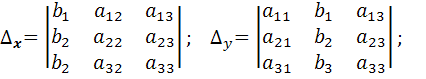
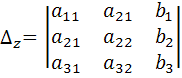Пример: 1. Решить систему уравнений методом Крамера.
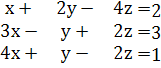
Вычислим главный определитель:
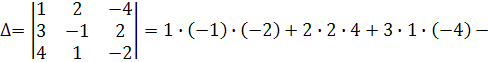
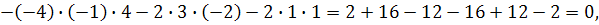
следовательно система не имеет решений.
Пример: 2.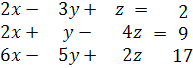 
Решение:
;
;
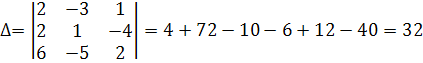
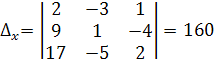
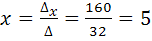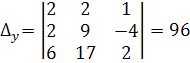
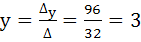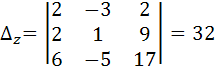
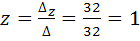
Решение систем линейных уравнений методом Гаусса:
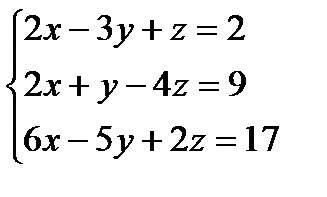
Постепенным исключением переменных находим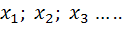 
Оставим первое уравнение неизменным. Исключим х из второго и третьего уравнений, вычтем из второго уравнения первое, а к третьему уравнению прибавим первое умноженное на (-3). Получим:
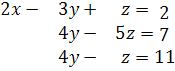
Оставим второе уравнение неизменным, исключив уиз третьего, умножив второе уравнение на (-1) и сложив с третьем уравнением получим.
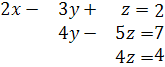
Из третьего уравнения найдем z
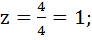
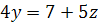
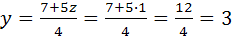
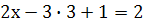
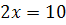
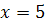
Ответ: 5; 3; 1.
Функция и пределы
Функция –зависимость, между двумя множествами Х и У, при котором одному элементу из множества Х поставлено в соответствие не более одного элемента из множества У.
Переменная у называется функцией переменной х.
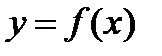Символически функциональная зависимость записывается с помощью равенства: . Множество всех действительных значений х, при которых функция существует называется областью определения функции.
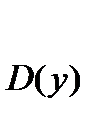Обозначается:
Пример: найти область определения функции: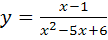 
Решение. Функция определена при всех значениях переменной х, кроме тех при которых знаменатель обращается в ноль. Решив уравнение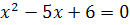 
, найдем его корни. Следовательно, функция определена на всей числовой прямой, кроме точек 
.
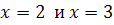Множество всех действительных значений у, которые может принимать функция называется множеством значений функции.
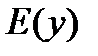Обозначается:
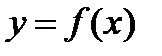Зависимость между аргументом x и функцией можно представить в виде некоторой линии.
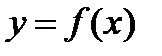Определение: графиком функции
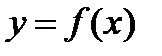называется множество всех точек плоскости, координаты которых удовлетворяют равенству .
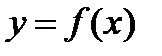Функция называется чётной,если перемена знака у аргумента не меняет значение функции, т. е.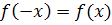 
График четной функции – кривая симметричная относительно оси ординат.
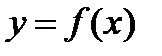Функция называется нечётной ,если перемена знака у аргумента изменяет только знак самой функции, т. е.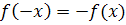 
График нечетной функции – кривая симметричная относительно начала координат.
Понятие предела переменной величины - одно из важнейших понятий математики.
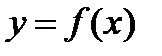§ Число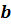 
называется пределом функции
при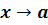 
, если для любой последовательности аргументов
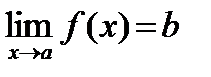сходящихся к 
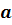, соответствующая последовательность значений функции сходится к .
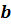Предел функции обозначается символом:
Функция называется бесконечно малой, если ее предел равен нулю
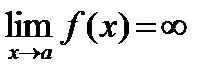Функция называется бесконечно большой, если ее предел равен бесконечности .
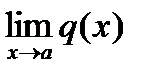
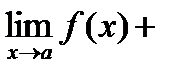
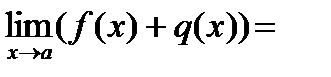Теоремы о пределах:
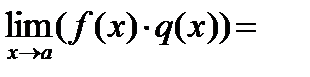
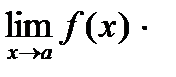
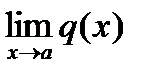
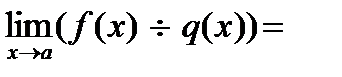
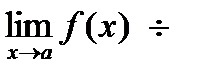
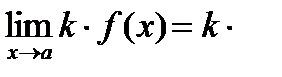
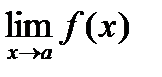
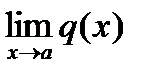
Следствия:
,
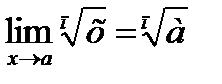
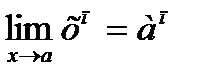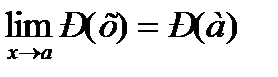
Примеры:
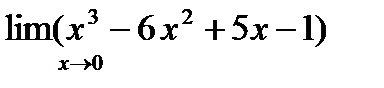1.Вычислить предел:
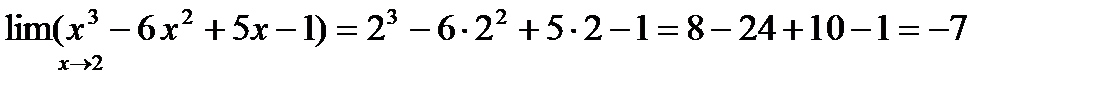По правилам нахождения предела многочлена находим
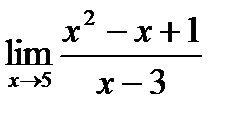
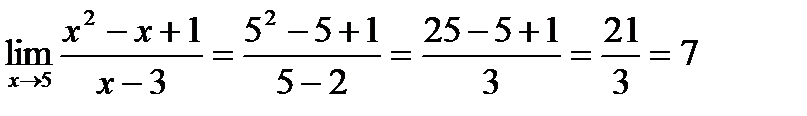2.Вычислить предел: , по правилам нахождения предела многочлена находим
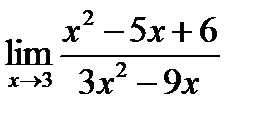
3.Вычислить предел:
В данном случае теорема о пределе частного частично не применима, т.к. при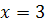 
, знаменатель равен нулю. Разложим числитель и знаменатель дроби на множител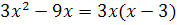и: 
и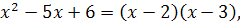 
Здесь 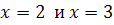корни уравнения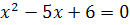
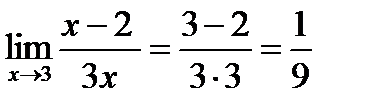
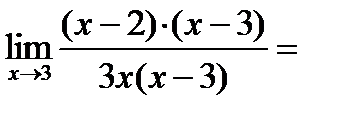
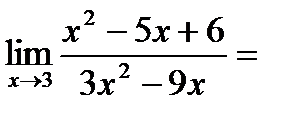4. Вычислить пределы:
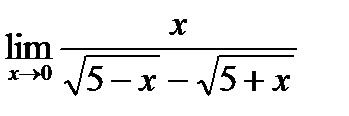1.
2.
умножим числитель и знаменатель дроби на выражение сопряженное знаменателю, т.е. на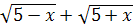 
, получим
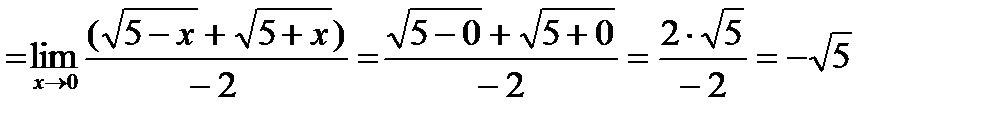
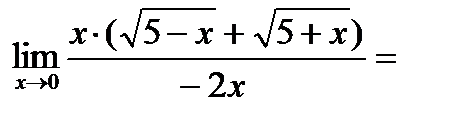
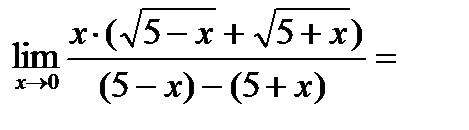
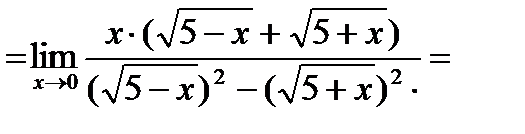
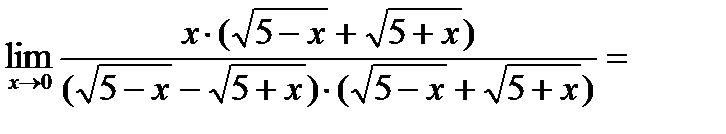
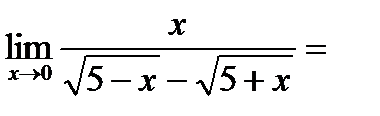
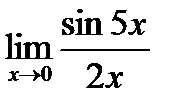
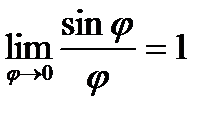5. Вычислить предел:
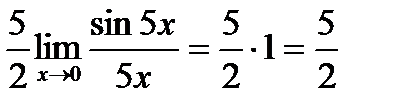
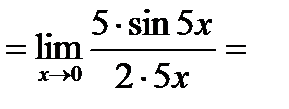
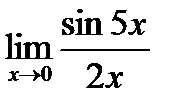Решение : используя первый замечательный предел
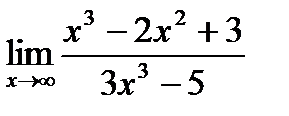имеем
6. Вычислить предел:
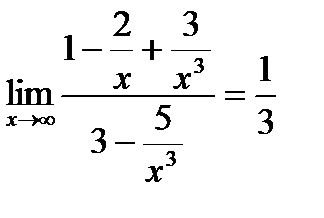
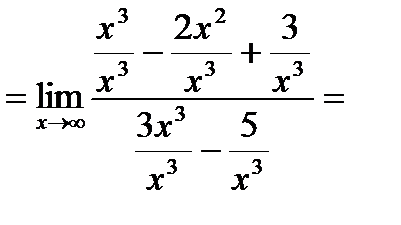Решение : разделим числитель и знаменатель дроби на 
,
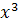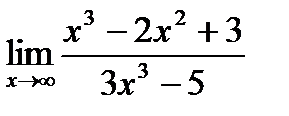
Здесь функци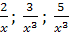и 
при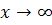 
бесконечно малы и их предел равен нулю.
Производная.
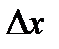
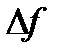Определение: Производной функции f(x) в точке называется предел отношения приращения функции в этой точке к
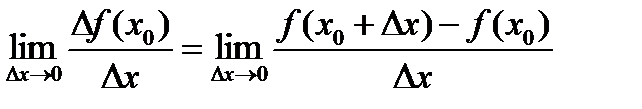приращению аргумента, когда
последнее стремится к нулю:
Обозначается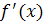 
, y’.
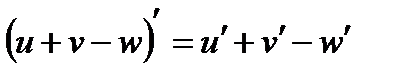Основные правила дифференцирования. (нахождения производной):
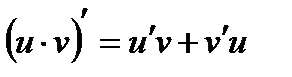- производная алгебраической суммы функций,
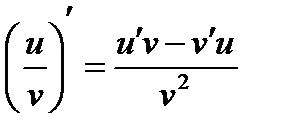- производная произведения двух функций,
- производная частного.
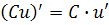
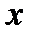Обозначения: С – постоянная; – аргумент.
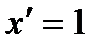
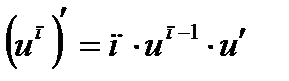
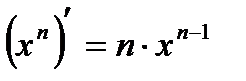Производные степени и корня:, С'=0,
,
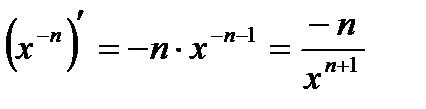
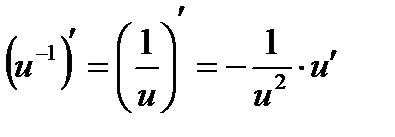
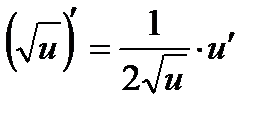
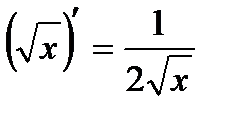
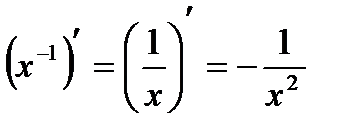
Физические приложения производной:
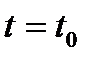
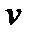При прямолинейном движении точки скорость в данный момент t есть производная от пути s по времени t, вычисленная при
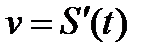
Ускорение движения точки находится по формуле:
.
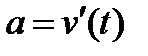Производные логарифмических и показательных функций:
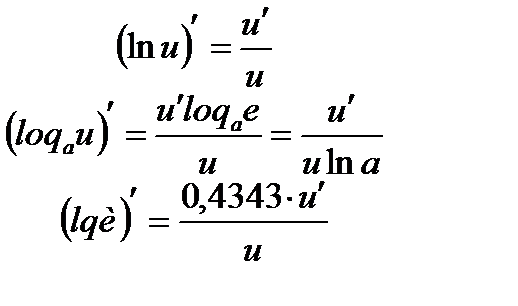
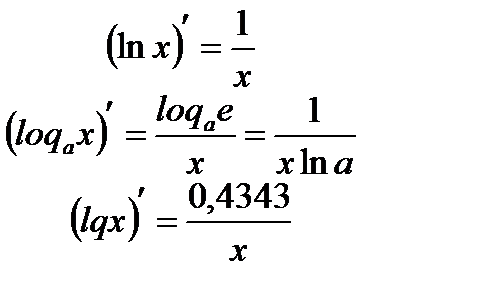
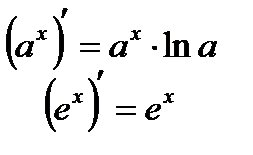
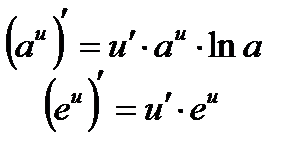
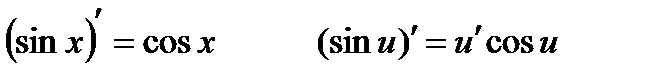Производные тригонометрических функций:
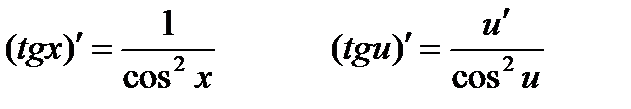
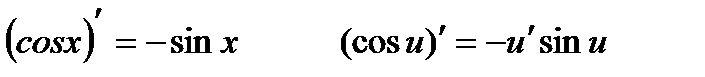
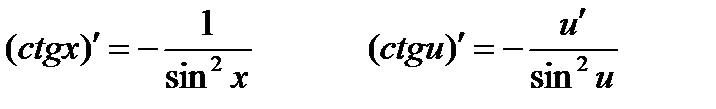
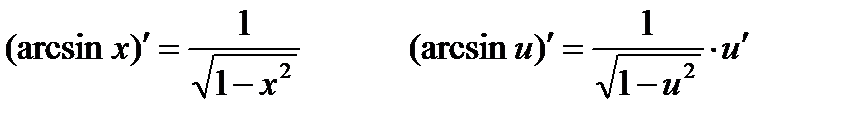Производные обратных тригонометрических функций:
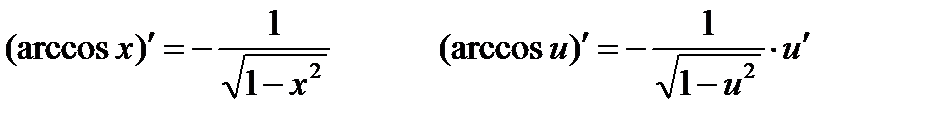
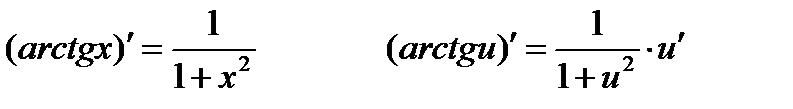
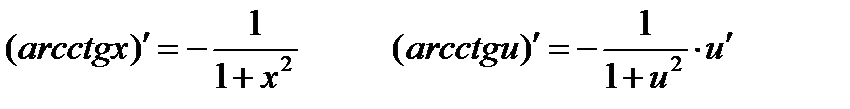
Примеры: применяя правила и формулы дифференцирования, найти производные следующих функций:
1. 
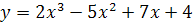
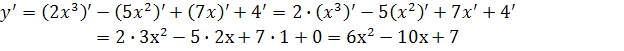
2. 
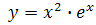
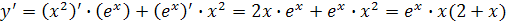
3. 
;
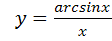
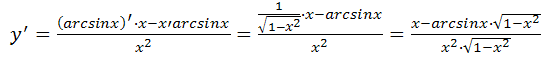4. 
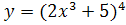
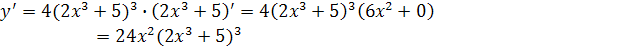
5. 
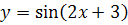
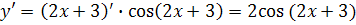
6. 
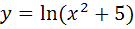
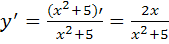
7. 
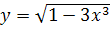
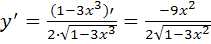
8. 
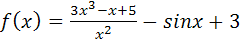
Приведем функцию к виду:
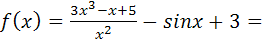
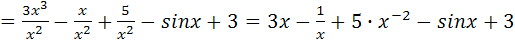, тогда
= 
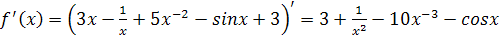