Определение и способ решения
Пусть  — некоторая функция,
— некоторая функция,  — ее производная. Для удобства будем записывать производную виде
— ее производная. Для удобства будем записывать производную виде  , имеющем смысл отношения бесконечно малых приращений — дифференциалов. Дифференциал
, имеющем смысл отношения бесконечно малых приращений — дифференциалов. Дифференциал  — приращение значения переменной в окрестности
— приращение значения переменной в окрестности  , стремящееся к нулю. Дифференциал функции
, стремящееся к нулю. Дифференциал функции  — малое приращение функции,
— малое приращение функции,  . Пусть
. Пусть 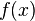 и
и  — некоторые функции от
— некоторые функции от  и
и  . Рассмотрим уравнение
. Рассмотрим уравнение
 .
.
Уравнение такого вида называется обыкновенным дифференциальным уравнением с разделяющимися переменными. Умножим его на  :
:
 .
.
Последнее равенство означает, что малые приращения левой и правой частей равны. Поэтому их суммы также равны. Предположим что при 
 и возьмем интегралы от левой и правой частей. Пределы интегрирования — от
и возьмем интегралы от левой и правой частей. Пределы интегрирования — от  до
до  для левой части и от
для левой части и от  для
для  для правой части уравнения:
для правой части уравнения:
 .
.
Решая получившееся в результате интегрирования алгебраическое уравнение, мы можем выразить  .
.
Значения  и
и  называются начальными условиями. В случае других начальных условий решение уравнения будет отличаться на постоянную. Поэтому, если начальные условия не даны, можно взять первообразные левой и правой частей и прибавить к ним константу. Используя неопределенный интеграл — обозначение множества первообразных —
называются начальными условиями. В случае других начальных условий решение уравнения будет отличаться на постоянную. Поэтому, если начальные условия не даны, можно взять первообразные левой и правой частей и прибавить к ним константу. Используя неопределенный интеграл — обозначение множества первообразных —  , где
, где  — первообразная
— первообразная 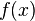 ,
,  — произвольная постоянная, запишем это в виде
— произвольная постоянная, запишем это в виде
 .
.
Следует отметить, что у дифференциального уравнения с разделяющимися переменными могут существовать так называемые нулевые решения — постоянные  , удовлетворяющие уравнению
, удовлетворяющие уравнению  . При них равны нулю как правая, так и левая части дифференциального уравнения (поскольку производная константы равна нулю).
. При них равны нулю как правая, так и левая части дифференциального уравнения (поскольку производная константы равна нулю).
2.3)
(О существовании и единственности решения задачи Коши). Пусть  - непрерывная функция в области
- непрерывная функция в области  , причем
, причем  - также непрерывен в
- также непрерывен в  . Тогда для любой точки
. Тогда для любой точки  задача Коши:
задача Коши:  имеет решение, причем единственное в том смысле, что если есть 2 ее решения
имеет решение, причем единственное в том смысле, что если есть 2 ее решения  и
и  , определенные на интервалах
, определенные на интервалах  и
и  , содержащих точку
, содержащих точку  , то они совпадают на пересечении
, то они совпадают на пересечении  этих интервалов.
этих интервалов.

Теорему оставим без доказательства.
Замечание. Говорят, что решение  дифференциального уравнения на интервале
дифференциального уравнения на интервале  есть продолжение решения
есть продолжение решения  на
на  , если
, если  и
и  на
на  . Также говорят, что решение
. Также говорят, что решение  - максимальное или непродолжаемое относительно
- максимальное или непродолжаемое относительно  , если
, если  не обладает продолжениями, целиком лежащими в
не обладает продолжениями, целиком лежащими в 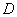 .
.
На основании этого замечания можно сказать, что при условиях теоремы существует единственное максимальное (непродолжаемое) решение задачи Коши.
Геометрический смысл сформулированной теоремы состоит в следующем. Левая часть уравнения  представляет собой
представляет собой  - тангенс угла наклона касательной к графику искомой функции в точке
- тангенс угла наклона касательной к графику искомой функции в точке  , а правая часть
, а правая часть  задает его численное значение
задает его численное значение  в этой точке. Поэтому можно считать, что уравнение задает поле направлений на области
в этой точке. Поэтому можно считать, что уравнение задает поле направлений на области 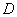 , т.е. к каждой точке
, т.е. к каждой точке  прикреплен вектор, указывающий направление касательной к искомой интергальной кривой.
прикреплен вектор, указывающий направление касательной к искомой интергальной кривой.
2.3)
