Дифференциал функции

Дифференциалом функции y=f(x), имеющей конечную производную 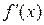, называется произведение её производной на приращение независимой переменной: /

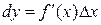Примечания:

1. В отличие от производной, величина которой может принимать как большие, так и малые значения в точке х, величина дифференциала всегда является малой и пропорциональной 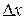(например, если 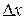уменьшается вдвое, то dy уменьшается вдвое).

2. Очевидно, что если функция имеет конечную производную в точке х, то она имеет и дифференциал, именно поэтому мы называем функцию дифференцируемой.

3. Дифференциал функции f(x) зависит от двух переменных: точки дифференцирования х и приращения 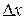в точке х.

Если 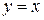, то , то 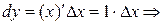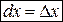есть дифференциал независимой переменной совпадает с ее приращением.

Поэтому 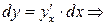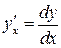, то есть производная функции равна отношению дифференциала функции к дифференциалу аргумента.

Пример 1.Найти дифференциал функции .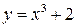

Решение. По формуле .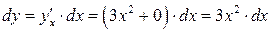

Основными свойствамидифференциала являются:

1) 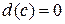, где с – константа.

2) .

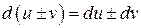3) .

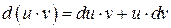4) .

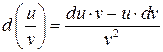Геометрический смысл дифференциала.

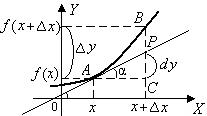
Дифференциал функции равен приращению ординаты точки касательной к графику y=f(x), когда аргумент 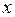получает приращение .

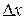Приближённые вычисления значений функций.

Практическое значение дифференциала: нахождение дифференциала функции позволяет определить, насколько изменяется эта функция при небольших изменениях переменной, от которой она зависит.

При достаточно малых 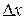верна приближённая формула:

(*)

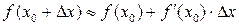При этом приближенные равенства тем точнее, чем меньше 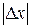, так как их погрешность есть величина более высокого порядка малости, чем .

----------------------------------------------------------------------------------------------------------------

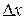Дифференциал функции. Стр. 1

Формулу (*) можно использовать для приближенного вычисления значения функции f(x) в "плохой" точке 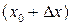, если известно ее значение в близкой "хорошей" точке .

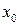Пример 2. Вычислить 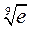при помощи дифференциала.

Решение. Вводим функцию 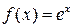. Требуется вычислить .

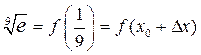Найдем ближайшую "хорошую" точку, в которой f(x) легко вычислить: 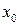= 0, тогда .

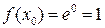Переходу от 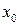к 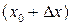соответствует приращение .

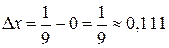Для применения формулы (*) найдем , .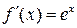

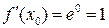В итоге получим 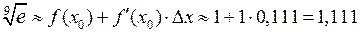.