Закон Ома в дифференциальной форме

Если проводник неоднороден по составу (неравномерно распределенные примеси), плотности или поперечному сечению, то применить формулу (6) не удастся. Поэтому выделим мысленно в окрестности некоторой точки внутри проводника элементарный цилиндрический объём, с образующими, параллельными вектору плотности тока j в данной точке (рис. 1).

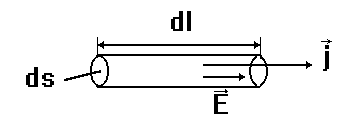
Рис. 1

Через поперечное сечение проводника течет ток силой jds. Разность потенциалов между концами цилиндра E dl, где Е- напряженность поля в данном месте. Сопротивление цилиндра, согласно (6), равно 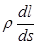. Подставив эти значения в формулы (2-6) получаем:

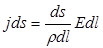(11)

Положительные носители заряда в каждой точке движутся в направлении вектора E. Поэтому направления векторов j и E совпадают. Таким образом, можно записать:

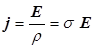(12)

где s - величина, называемая коэффициентом электропроводности или проводимостью материала. В отличие от интегральной формы закона Ома дифференциальная форма содержит величины, характеризующие электрическое состояние среды в одной точке.