Матричное 2х2 представление геометрических преобразований

В общем случае преобразования на плоскости (Слайд 7) представляют в виде линейных зависимостей новых координат от старых. Такие преобразования удобно переписывать в матричной форме: векторная строка из двух компонентов в виде старых (стартовых) координат x, y умножается на матрицу 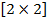, элементы которой – коэффициенты при линейных координатах, связанных с преобразованиями масштабирования, поворота и сдвига. К ним добавлена вектор-строка коэффициентов, связанных с параллельным переносом.

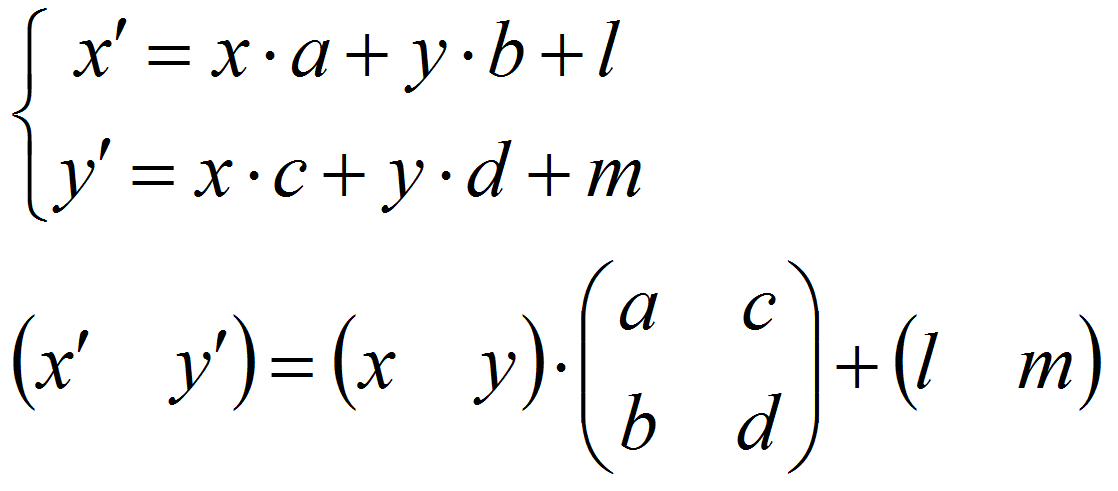
В практике удобно избавиться от слагаемого, связанного с параллельным переносом, и представить всё в виде матрицы, которая обеспечивает все четыре вида преобразований.

Матричная запись удобна. Лучше иметь единое произведение исходного вектора с координатами точки на матрицу преобразования, чем выражение в виде суммы разных слагаемых.

3. Однородные координаты и геометрические преобразования: слайд 8

Для преобразования матрицы аффинных преобразований к более удобному виду принято рассматривать так называемые однородные координаты. Эта тема (теория) рассматривается в проективной геометрии.

Суть преобразования состоит во введении в оборот дополнительной координаты. Формально - обычной паре координат x и y на плоскости ставится в соответствие тройка координат в некотором трёхмерном пространстве:

. .

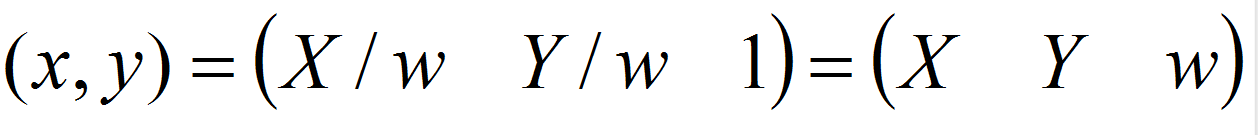Пусть W=1, тогда тройка координат получит вид

(x,y) = (x, y, 1)

А матричные преобразования 2х2 можно видоизменить, записав их с помощью однородной координаты в виде матрицы 3х3, добавив третью строку и третий столбец.

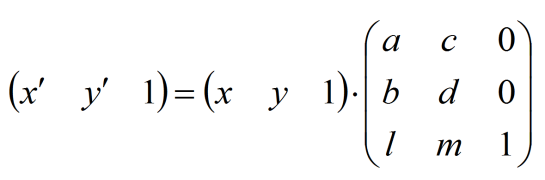
В качестве третьей координаты добавлена компонента W (обозначение может быть разным h, S, H и т. п.). Эту компоненту можно считать нормирующим множителем. Применение однородных координат даёт ряд плюсов.

1.Используя координату W как нормирующий множитель можно получать удобную форму для хранения в памяти машины значений координат в более рациональном виде.

2.Все преобразования, что были записаны раньше, могут быть пересчитаны также в более удобном виде как единое произведение матрицы–строки координат на матрицу преобразования.

Слагаемое, связанное с параллельным переносом может быть занесено в 3-ю строку, в предположении, что W=1.

На самом деле параллельный перенос не влияет на свободный вектор и его применяют только к радиус-вектору, который задаёт отдельную точку на плоскости (или в пространстве).

Если W=0, то получим точку в бесконечности, т. е. получим направление радиус-вектора, указывающего, где может находиться точка в бесконечности (например, направление полёта снаряда). Этим пользуются (приравнивая W=0) и когда надо показать отличие радиус-вектора от точки или получить направление радиус-вектора к точке в бесконечности.

Запись: W=1 = > X, Y, W – это точка, а запись: W=0 = > X, Y, 0 – это свободный вектор или его направление.

Если в уравнении преобразования подставить W=0, то никакого параллельного переноса мы не получим, но возможно масштабирование, поворот и сдвиг объекта по линии направления свободного вектора.

Перепишем все, ранее составленные матрицы преобразования с добавлением однородных координат. Вот что из этого получается: (Слайд 9)

~ translation (перенос)

T(dx, dy) =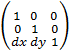

Сдвиг

~ shear by x (сдвиг по x)

sh_x (sh_x) =

~ shear by y (сдвиг по y)

Sh_y (sh_y) =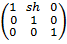

~ scaling (масштабирование)

S (s_x, s_y) =

~ rotation (вращение)

R (α) =

Все матрицы получились 3×3, все матрицы квадратные, все преобразования имеют обратное представление (обратные матрицы). Определитель всех матриц detA ≠ 0 и преобразования можно осуществлять как в одну сторону, так и в другую.