II. Краткая теория исследуемого явления

На проводник с током в магнитном поле действует сила. Обобщая опытные данные, Ампер установил, что сила 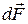, с которой магнитное поле действует на элемент проводника dl с током I, равна

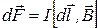, (1)

где 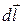– вектор по модулю, равный dl и совпадающий по направлению с током, 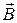– вектор магнитной индукции.

Направление силы 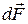можно найти по правилу векторного произведения или по правилу левой руки: если ладонь левой руки расположить так, чтобы линии вектора 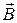входили в нее, а четыре вытянутых пальца направить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы Ампера.

Численное значение силы Ампера можно найти, раскрыв векторное произведение:

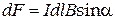, (2)

где 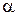– угол между векторам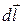и и .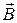

Для расчета силы Ампера, действующей на проводник заданной длины и формы, надо разделить проводник на прямолинейные участки 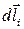столь малые, чтобы магнитное поле в пределах любого участка было однородно, а затем, используя формулу (1), вычислить силы 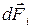и просуммировать их:

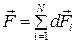или .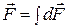

Из закона Ампера можно установить физический смысл вектора магнитной индукции (см. лаб. работу 32) и единицу его измерения.

Единица магнитной индукции в СИ называется тесла (Тл). Один Тл равен магнитной индукции однородного магнитного поля 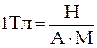, в котором на проводник длиной 1м с током в 1 А, расположенный перпендикулярно линиям индукции магнитного поля, действует сила, равная одному Ньютону.

Для характеристики магнитного поля, кроме вектора магнитной индукции 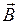, используют векторную величину 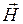, называемую напряженностью магнитного поля. Вектора 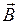и 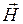связаны соотношением

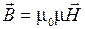, (3)

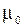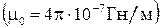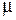где – магнитная постоянная , а – магнитная проницаемость вещества, которая зависит от свойств среды. Для вакуума 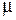=1.

Единица напряженности магнитного поля в СИ носит название ампер на метр (А/м).

Закон Ампера применяется для расчетов при конструировании электродвигателей, электроизмерительных приборов, магнитных реле, соленоидов для получения сильных магнитных полей и т.д.