Пример синтеза регулятора скорости
Пример 3.1 ( 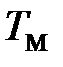 >
> 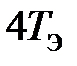 ).Рассчитать параметры и электрическую схему аналогового ПИД-регулятора. Для расчёта использовать данные, рассчитанные в примере 2.2а. Выбрать RC-элементы и операционный усилитель.
).Рассчитать параметры и электрическую схему аналогового ПИД-регулятора. Для расчёта использовать данные, рассчитанные в примере 2.2а. Выбрать RC-элементы и операционный усилитель.
Решение.Поскольку, 4Тэ меньше чем Тм, то передаточную функцию регулятора скорости представим в виде
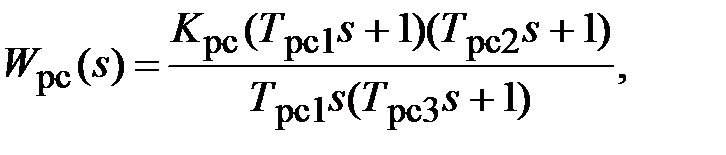
где постоянные времени 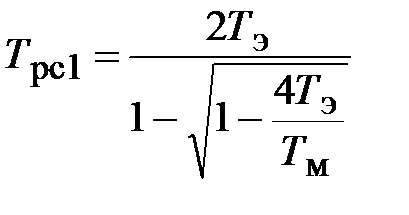 ,
, 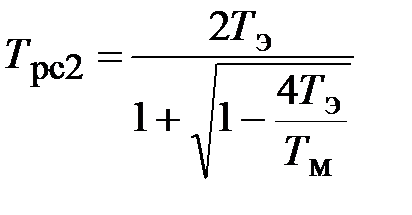 ,
, 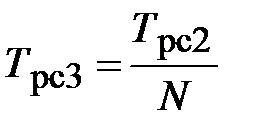 , коэффициент передачи
, коэффициент передачи 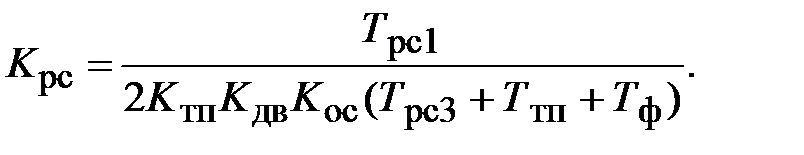
На основании схемы, представленной на рис. 3.9, постоянные времени и коэффициент передачи ПИД-регулятора скорости определяются по формулам:
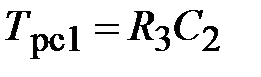 ;
; 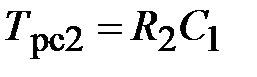 ;
; 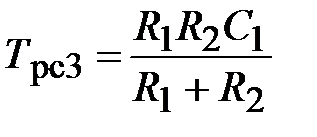 ;
; 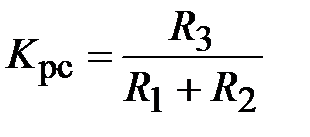 . (3.21)
. (3.21)
Рис. 3.9. Электрическая схема ПИД-регулятора скорости
Заметим, что в формулах (3.21) число неизвестных 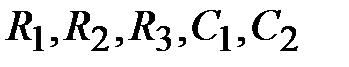 превышает число уравнений. Поэтому в инженерной практике прибегают к способу, когда значении емкостей назначаются из стандартного ряда 1; 10; 22; 33; 47; 100 мкФ. Тогда порядок расчета сводится к следующему.
превышает число уравнений. Поэтому в инженерной практике прибегают к способу, когда значении емкостей назначаются из стандартного ряда 1; 10; 22; 33; 47; 100 мкФ. Тогда порядок расчета сводится к следующему.
1. Задаемся емкостью 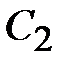 и рассчитываем
и рассчитываем 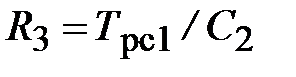 .
.
2. Задаемся емкостью 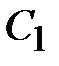 и рассчитываем
и рассчитываем 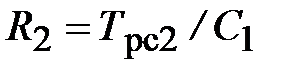 .
.
3. Согласно формулы 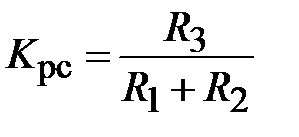 сопротивление
сопротивление 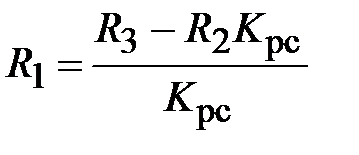 .
.
Приводим сопротивления 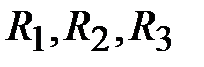 к номинальным значениям по ряду Е192 (табл. П5). Необходимо отметить, что при этом коэффициент передачи регулятора может измениться. В этой связи сопротивление
к номинальным значениям по ряду Е192 (табл. П5). Необходимо отметить, что при этом коэффициент передачи регулятора может измениться. В этой связи сопротивление 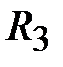 выбирается переменным, чтобы соответствующей его подстройкой выставить расчетное значение
выбирается переменным, чтобы соответствующей его подстройкой выставить расчетное значение 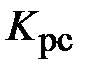 .
.
Переходим к расчету номинальных значений RC-элементов.
Постоянные времени РС
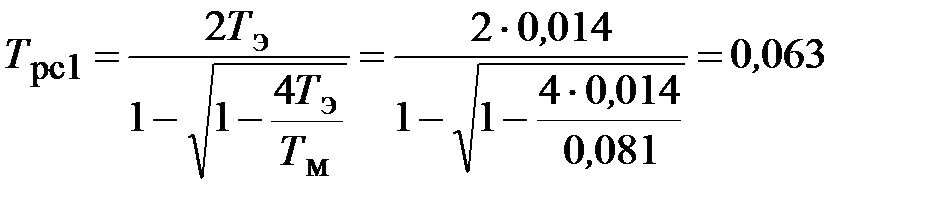 с;
с;
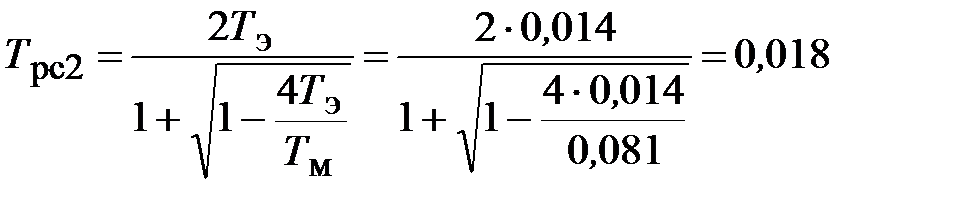 с;
с;
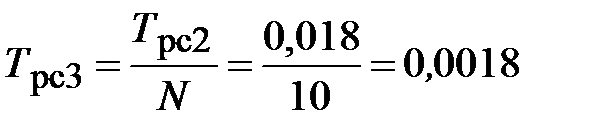 с.
с.
Коэффициент передачи регулятора скорости
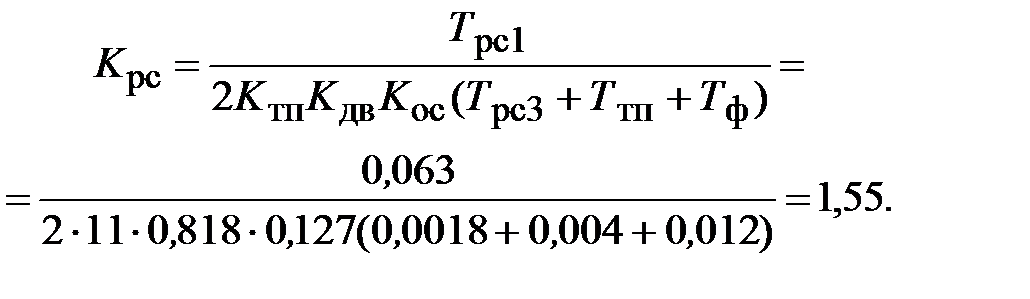 (3.22)
(3.22)
Задаем 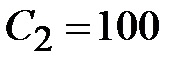 мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда
мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда
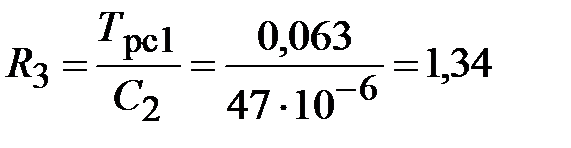 кОм.
кОм.
Приводим сопротивление к номинальному значению по ряду Е192 (см. табл. П5) и принимаем 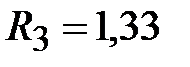 кОм.
кОм.
Задаем 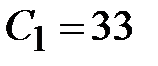 мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда
мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда
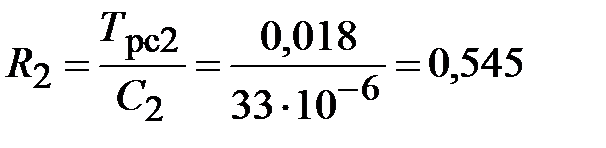 кОм.
кОм.
Приводим сопротивление к номинальному значению по ряду Е192 (см. табл. П5) и принимаем 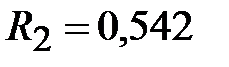 кОм.
кОм.
Рассчитываем сопротивление
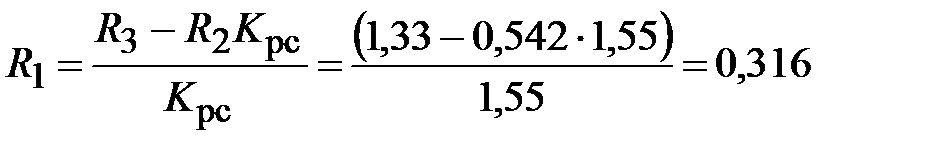 кОм.
кОм.
Приводим сопротивление к номинальному значению по ряду Е192 (см. табл. П5) и принимаем 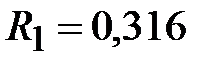 кОм.
кОм.
По полученным номинальным значениям сопротивлений РС пересчитываем коэффициент передачи
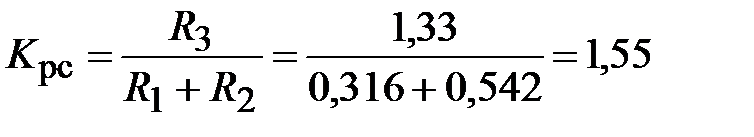 .
.
Полученное значение не отличается от величины коэффициента передачи 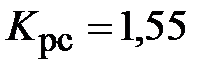 , рассчитанного по формуле (3.22), поэтому подстройки резистора
, рассчитанного по формуле (3.22), поэтому подстройки резистора  не требуется.
не требуется.
Пример 3.2.Провести моделирование КС с аналоговым ПИД-регулятором скорости по примеру 2.2а. Получить графики переходных функций по задающему воздействию и по моменту сопротивления нагрузки 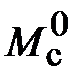 . Построить график ЛЧХ разомкнутого КС. Провести анализ результатов моделирования.
. Построить график ЛЧХ разомкнутого КС. Провести анализ результатов моделирования.
Решение.Для моделирования построим ССДМ КС в системе Simulink, представленную на рис. 3.10.
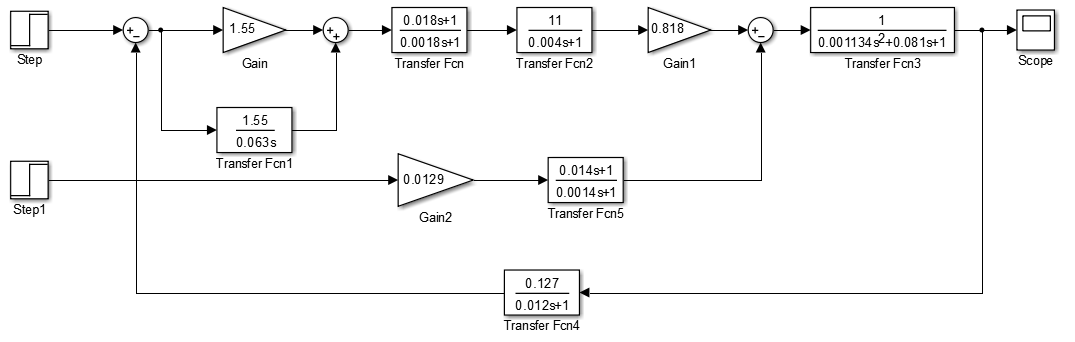
Рис. 3.10. Структурная схема динамической модели контура скорости
в системе Simulink
В блоке Step задаём воздействие, равное входному напряжению суммирующего усилителя КС 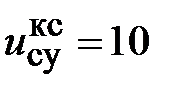 В, а в блоке Step 1 значение момента сопротивления нагрузки
В, а в блоке Step 1 значение момента сопротивления нагрузки 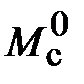
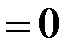 . На рис. 3.11 изображен график переходной характеристики контура скорости по управляющему воздействию.
. На рис. 3.11 изображен график переходной характеристики контура скорости по управляющему воздействию.
Для построения переходной характеристики по моменту сопротивления нагрузки Мс устанавливаем соответственно в блоке Step входное воздействие 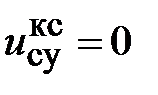 , а в блоке Step 1 – момент сопротивления
, а в блоке Step 1 – момент сопротивления 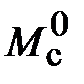
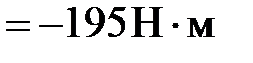 . Полученная зависимость представлена на рис. 3.12.
. Полученная зависимость представлена на рис. 3.12.
Ω(t), рад/с
 t, c
t, c
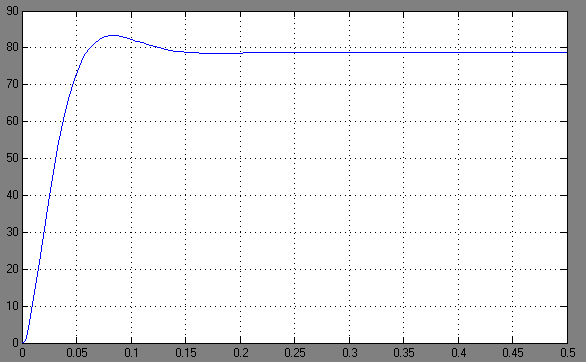
Рис. 3.11. График зависимости угловой скорости от времени скорректированного контура скорости по сигналу задания
Ω(t), рад/с
 t, c
t, c
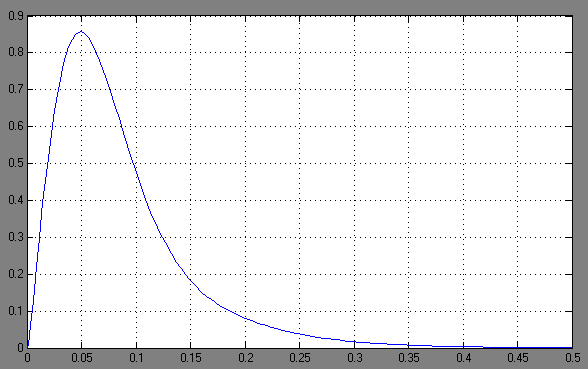
Рис. 3.12. График зависимости угловой скорости от времени скорректированного контура скорости по моменту сопротивления
Переходим к анализу полученных графиков. По графику на рис. 3.11 определяем максимальное значение угловой скорости вращения двигателя Ωmax = 83 рад/с и установившееся значение скорости Ωуст = 78,74 рад/с. По этим данным рассчитываем перерегулирование
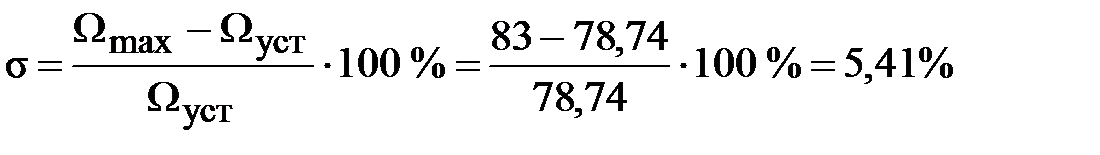 .
.
Перерегулирование, полученное в результате моделирования, отличается от требуемого значения 4,3 %. Такое изменение обусловлено влиянием малой постоянной времени Тф. Если принять Тф = 0, то перерегулирование будет равно 4,3 %, а передаточная функция ТГ представится безынерционным звеном
Wос(s) = Кос.
При этом суммарную малую постоянную времени КС следует рассчитывать по формуле
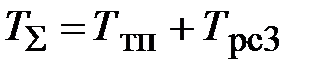 .
.
Время нарастания 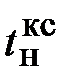 определяется в первой точке пересечения графика переходной функции и установившегося значения угловой скорости Ωуст и составляет
определяется в первой точке пересечения графика переходной функции и установившегося значения угловой скорости Ωуст и составляет
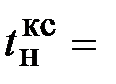 0,06 с.
0,06 с.
Проверяем соответствие полученного значения требованиям настройки на ОМ
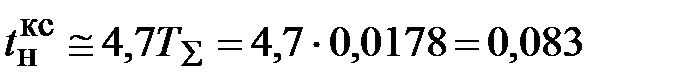 с.
с.
Из анализа графика на рис. 3.12 следует, что при воздействии неизменного по величине момента сопротивления Мс моментная составляющая ошибки ΔΩм примерно через 0,45 с становится равной нулю. Это говорит о том, что искусственная механическая характеристика стала абсолютно жёсткой. Увеличение точности обусловлено наличием в структуре регулятора скорости интегральной составляющей.
Для построения ЛЧХ необходимо написать программу в Command Window среды MatLab. Поскольку ЛЧХ строятся на основе передаточной функции разомкнутого контура скорости, то все передаточные функции соответствующих элементов, входящих в него, необходимо перемножить и получить
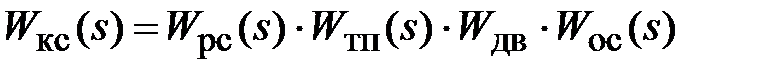 .
.
Обозначая Wрс(s) = sys1, Wтп(s) = sys2, Wдв(s) = sys3, Wос(s) = sys4, составляем программу в соответствии со следующим алгоритмом:
num1 = [KpcTpc1Tpc2 (Tpc1+Tpc2)Kpc Kpc];
den1 = [Tpc1Tpc3 Tpc1 0];
sys1 = tf(num1, den1)
num2 = [Kтп];
den2 = [Tтп 1];
sys2 = tf(num2, den2)
num3 = [Kдв];
den3 = [TэTм Tм 1];
sys3 = tf(num3, den3)
num4 = [Kос];
den4 = [Tф 1];
sys4 = tf(num4, den4)
sys5 = sys1*sys2*sys3*sys4
В результате решения будет получена искомая передаточная функция разомкнутого КС с численными значениями коэффициентов полиномов числителя и знаменателя b2, b1, b0, d6, d5, d4, d3, d2, d1, d0 = 0
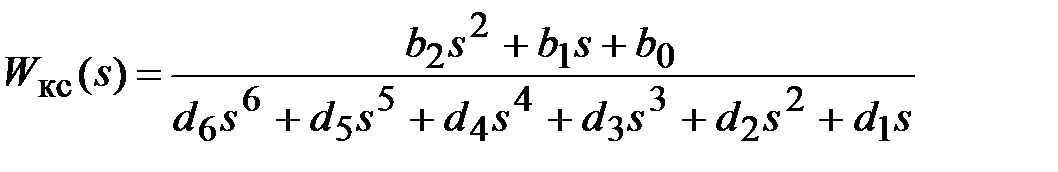 .
.
Далее переходим к построению ЛЧХ:
num = [b2 b1 b0];
den = [d6 d5 d4 d3 d2 d1 0];
bode(num, den)
Перед тем как применить программу построения ЛЧХ, находим соответствующие коэффициенты из блоков Transfer Fcn, Transfer Fcn1, Gain, Transfer Fcn2, Transfer Fcn3 схемы, изображённой на рис. 3.10:
num1=[0.0017577 0.12555 1.55];
den1=[0.0001134 0.063 0];
sys1=tf(num1, den1);
num2=[11];
den2=[0.004 1];
sys2=tf(num2, den2);
num3=[0.818];
den3=[0.001134 0.081 1];
sys3=tf(num3, den3);
num4=[0.127];
den4=[0.012 1];
sys4=tf(num4, den4);
sys5=sys1*sys2*sys3*sys4
sys5 =
0.002009 s^2 + 0.1435 s + 1.771
--------------------------------------------------------------------------------------
6.173e-12 s^6 + 5.928e-09 s^5 + 1.669e-06 s^4 + 0.0001671 s^3 + 0.006224 s^2 + 0.063 s
num=[0.002009 0.1435 1.771];
den=[6.173e-12 5.928e-09 1.669e-06 0.0001671 0.006224 0.063 0];
bode(num, den)
Результаты моделирования представлены на рис. 3.12.
Из анализа графиков видно, что запасы устойчивости по фазе и амплитуде составляют Lз = 17,8 дБ (Gain Margin) и 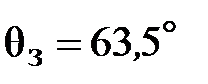 (Phase Margin) соответственно.
(Phase Margin) соответственно.
Напомним, что запас устойчивости по амплитуде Lз определяется как разность между линией 0 дБ и значением логарифмической амплитудно-частотной характеристики (ЛАЧХ) на частоте, соответствующей точке пересечения графика фазовой частотной характеристики со значением –180°.
Запас устойчивости по фазе 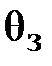 вычисляется по формуле
вычисляется по формуле
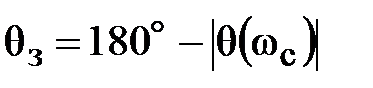 .
.
Значение фазы 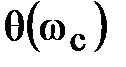 соответствует частоте среза ωс, т. е. точке пересечения графика ЛАЧХ с линией 0 дБ.
соответствует частоте среза ωс, т. е. точке пересечения графика ЛАЧХ с линией 0 дБ.
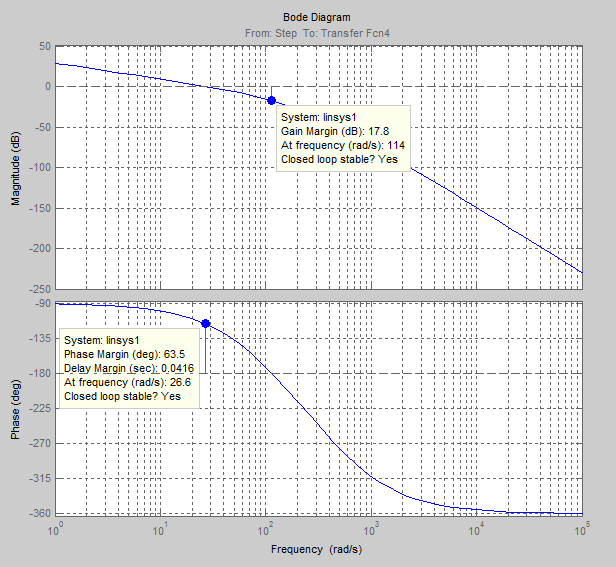
Рис. 3.12. Логарифмические частотные характеристики контура скорости
Результаты моделирования подтверждают правильность расчёта параметров РС и позволяют сделать вывод о том, что КС настроен на ОМ.
Задача построения ЛЧХ может решаться с применением приложения Linear Analysis Tool. Для этого необходимо выполнить следующие операции:
- определить вход и выход разомкнутого КС по рис. 3.10;
- нажать правой клавишей мыши на линию связи блоков Step и первого сумматора, и во вкладке Linear Analysis Points отметить Input Point;
- на выход разомкнутого КС установить блок Terminator и на соответствующей линии связи отметить Output Point;
- на панели инструментов окна модели открыть вкладку Analysis и в строке Control Design выбрать Linear Analysis;
- в окне Linear Analysis Tool в строке Plot Result выбрать Bode Plot, нажать пиктограмму Linearize и получить графики ЛЧХ.
Отчётные материалы
1. Расчет параметров структурной схемы динамической модели контура скорости.
2. Расчет параметров аналогового регулятора скорости.
3. Электрическая схема аналогового регулятора скорости.
4. Структурная схема динамической модели контура скорости.
5. Графики зависимостей угловой скорости от времени скорректированного контура скорости по сигналу задания и моменту сопротивления и их анализ.
6. ЛЧХ и их анализ.
Контрольные вопросы
1. Дать определение настройки на ОМ.
2. Дать определение настройки на СО.
3. Записать передаточную функцию замкнутого контура настроенного
на ОМ.
4. Записать передаточную функцию разомкнутого контура настроенного на СО.
5. Перечислить показатели качества переходного процесса с применением стандартных настроек.
6. Записать передаточную функцию ПИД-регулятора.
7. Начертить электрическую схему ПИД-регулятора.
8. Изложить порядок моделирования контура скорости с применением системы MatLab.
ЛАБОРАТОРНАЯ РАБОТА № 4
