БИЛЕТ№14
Ток смещения. Максвелл выдвинул идею: поскольку меняющееся во времени магнитное поле (  ) создает электрическое поле в соответствии с открытием Фарадея, то следует ожидать, что меняющееся во времени электрическое поле (
) создает электрическое поле в соответствии с открытием Фарадея, то следует ожидать, что меняющееся во времени электрическое поле (  ) создает магнитное поле. К этой идее можно прийти путем, например, следующих рассуждений. Выразим в теореме о циркуляции вектора
) создает магнитное поле. К этой идее можно прийти путем, например, следующих рассуждений. Выразим в теореме о циркуляции вектора  (90) ток как поток вектора плотности тока (36):
(90) ток как поток вектора плотности тока (36):
 . (110)
. (110)
 Применим эту теорему к случаю, когда предварительно заряженный плоский конденсатор разряжается через некоторое внешнее сопротивление (рис.37). В качестве контура Г возьмем периметр квадрата S, перпендикулярного проводу. Достроим квадрат до куба, так, чтобы грань параллельная S проходила внутри конденсатора. Пусть поверхность
Применим эту теорему к случаю, когда предварительно заряженный плоский конденсатор разряжается через некоторое внешнее сопротивление (рис.37). В качестве контура Г возьмем периметр квадрата S, перпендикулярного проводу. Достроим квадрат до куба, так, чтобы грань параллельная S проходила внутри конденсатора. Пусть поверхность 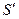 состоит из суммы всех граней куба, кроме грани S. Очевидно, обе поверхности, S и
состоит из суммы всех граней куба, кроме грани S. Очевидно, обе поверхности, S и 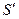 имеют одну границу - контур Г. Однако через поверхность
имеют одну границу - контур Г. Однако через поверхность  течет ток I, а через поверхность
течет ток I, а через поверхность 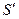 не течет никакого тока. Получается, что в (110) справа интеграл через поверхность
не течет никакого тока. Получается, что в (110) справа интеграл через поверхность 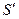 равен нулю, а через поверхность
равен нулю, а через поверхность  - току I. Т.е. теорема о циркуляции вектора
- току I. Т.е. теорема о циркуляции вектора  выполняется не для любой поверхности, ограниченной одним и тем же контуром Г, охватывающим ток. Чтобы избежать этой неприятности, заметим, что сквозь поверхность
выполняется не для любой поверхности, ограниченной одним и тем же контуром Г, охватывающим ток. Чтобы избежать этой неприятности, заметим, что сквозь поверхность 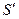 проходит только электрическое поле (через ту ее часть, которая находится внутри конденсатора). Продифференцируем теорему Гаусса для вектора электрического смещения
проходит только электрическое поле (через ту ее часть, которая находится внутри конденсатора). Продифференцируем теорему Гаусса для вектора электрического смещения  (78) по времени:
(78) по времени:  . С другой стороны, согласно уравнению непрерывности
. С другой стороны, согласно уравнению непрерывности
 . Сложив два последних уравнения, получим
. Сложив два последних уравнения, получим
 . (111)
. (111)
В этом выражении плотность тока проводимости складывается с производной по времени от вектора 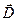 , которую Максвелл назвал плотностью тока смещения
, которую Максвелл назвал плотностью тока смещения
 . (112)
. (112)
Сумму тока смещения и тока проводимости называют полным током, Плотность полного тока равна
 . (113)
. (113)
Таким образом, линии плотности тока проводимости замыкаются линиями плотности тока смещения.
Теперь убедимся в том, что введение полного тока устраняет трудность, связанную с зависимостью циркуляции вектора  от выбора поверхности, ограниченной контуром Г. Введем в правую часть (110) полный ток
от выбора поверхности, ограниченной контуром Г. Введем в правую часть (110) полный ток
 . (114)
. (114)
Покажем, что полный ток будет одинаков для поверхностей  и
и 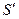 . Применим уравнение (111) к замкнутой поверхности
. Применим уравнение (111) к замкнутой поверхности  +
+ 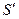 (полной поверхности куба на рис.37), с учетом того, что для замкнутой поверхности положительная нормаль направлена везде наружу
(полной поверхности куба на рис.37), с учетом того, что для замкнутой поверхности положительная нормаль направлена везде наружу
 . (115)
. (115)
Знак минус появился из-за того, что нормали (  ) для
) для 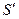 и
и 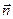 для
для  (рис.37, b) направлены в противоположные стороны. Отсюда следует, что
(рис.37, b) направлены в противоположные стороны. Отсюда следует, что
 , (116)
, (116)
что и требовалось доказать. Именно таким образом теорему о циркуляции вектора  , сформулированную ранее для постоянных токов, следует обобщить для произвольного случая и записать
, сформулированную ранее для постоянных токов, следует обобщить для произвольного случая и записать
 . (117)
. (117)
В таком виде теорема о циркуляции вектора  справедлива всегда, о чем свидетельствуют результаты эксперимента во всех без исключения случаях.
справедлива всегда, о чем свидетельствуют результаты эксперимента во всех без исключения случаях.
Несколько замечаний о токе смещения. Ток смещения эквивалентен току проводимости только в отношении способности создавать магнитное поле. Токи смещения существуют там, где меняется со временем электрическое поле.
Теорема и циркуляции вектора  (для магнитного поля постоянных токов). В магнетиках циркуляция вектора
(для магнитного поля постоянных токов). В магнетиках циркуляция вектора 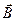 будет определяться не только токами проводимости, но и токами намагничивания:
будет определяться не только токами проводимости, но и токами намагничивания:
 . (93)
. (93)
Так как определение токов намагничивания 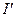 сложная задача, удобно ввести вспомогательный вектор (
сложная задача, удобно ввести вспомогательный вектор (  ), циркуляция которого будет определяться только токами проводимости внутри контура Г. Согласно (92) циркуляция вектора
), циркуляция которого будет определяться только токами проводимости внутри контура Г. Согласно (92) циркуляция вектора 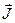 равна сумме токов намагничивания
равна сумме токов намагничивания  ® (87), Þ
® (87), Þ
 , Þ
, Þ
 , (94)
, (94)
где циркуляция вспомогательного вектора  =
=  определяется только токами проводимости
определяется только токами проводимости 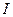 . В некоторых учебниках вектор
. В некоторых учебниках вектор  называется напряженностью магнитного поля. Итак,
называется напряженностью магнитного поля. Итак,
 , Þ (95)
, Þ (95)
теорема о циркуляции вектора  выглядит так. Циркуляция вектора
выглядит так. Циркуляция вектора  по произвольному замкнутому контуру Гравна алгебраической сумме токов проводимости, охватываемых этим контуром:
по произвольному замкнутому контуру Гравна алгебраической сумме токов проводимости, охватываемых этим контуром:
 . (96)
. (96)
