Согласно классическому определению вероятности 1 страница

ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ

КОНТРОЛЬНОЙ РАБОТЫ

Студенты ВВиДО выполняют одну контрольную работу по курсу "Теория вероятностей и математическая статистика". Контрольная работа содержит 7 заданий.

Номер варианта следует выбрать по первой букве фамилии студента в соответствии с данной таблицей:

Первая буква фамилии студента	Вариант контрольной работы
А, Б	№ 12
В, Г	№ 11
Д, Е, Ж	№ 10
З, И	№ 9
К	№ 8
Л, М	№ 7
Н, О	№ 6
П, Р	№ 5
С, Т	№ 4
У, Ф, Х	№ 3
Ц, Ч, Ш	№ 2
Щ, Э, Ю, Я	№ 1

Контрольная работа, выполненная не по своему варианту, к зачету не принимается.

На титульном листе надо разборчиво написать свою фамилию и инициалы, название факультета, специальности и номер варианта.

Перед решением задачи необходимо указать ее номер и записать полностью ее условие.

Решение задачи следует излагать подробно с объяснением всех действий.

После получения отрецензированной работы студент должен исправить все отмеченные ошибки или недочеты в той же тетради и явиться на собеседование. Если есть задачи, выполненные неверно, студенту необходимо переделать их и прислать работу повторно.

Образец выполнения контрольной работы

Задание 1. В ящике 12 писем, из них 7 иногородних и 5 городских. Какова вероятность того, что среди вынутых наудачу 4 писем окажется:

а) только одно городское;

б) городских и иногородних поровну.

Литература: 1, гл. 1. С. 7-13.

2, гл. 1. С. 7-9.

Решение. а) Пусть событиеА - среди вынутых 4 писем только одно городское.

Согласно классическому определению вероятности

,

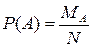где N - число всех равновозможных, единственно возможных и несовместных исходов; M_A - число исходов, благоприятствующих событию А.

В нашем случае 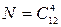- число всевозможных сочетаний из 12 писем по 4 письма.

Найдем число исходов, благоприятствующих событию А. Так как среди вынутых четырех писем будет только одно городское, то остальные три будут иногородние. Число способов, которыми можно вынуть одно письмо из пяти городских, равно 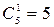. Три иногородних письма берут из имеющихся семи писем. Число сочетаний из семи по три равно 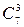. При этом каждое городское письмо может появиться с любой тройкой иногородних, поэтому

.

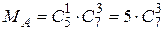Таким образом, .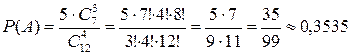

б) Пусть событие B - среди вынутых 4 писем городских и иногородних поровну. Вероятность событияВ

,

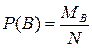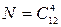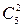где (см. пункт а); число исходов, благоприятствующих событиюВ, , так как каждая пара городских писем может появиться с любой парой иногородних. При этом два письма из пяти городских можно выбрать способами, а два письма из семи иногородних - .

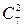Тогда .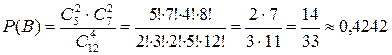

Задание 2. Вероятности того, что нужная сборщику деталь находится в первом, втором и третьем ящике, равны 0,5; 0,8; 0,6, соответственно. Найти вероятность того, что нужная деталь содержится:

а) во всех трех ящиках;

б) только в одном ящике;

в) по крайней мере, в одном ящике.

Литература: 1, гл. 2. С. 14-23.

2, гл. 1. С. 12-18.

Решение. Введем обозначения:

событие 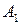- нужная деталь содержится в первом ящике;

событие 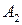- нужная деталь содержится во втором ящике;

событие 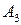- нужная деталь содержится в третьем ящике.

По условию ; ; .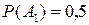

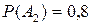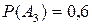а) Пусть событиеА - нужная деталь содержится во всех трех ящиках. Это событие является произведением событ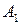ий 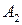, и , и 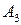, то есть .

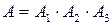Учитывая, что события 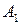, , 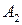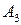- независимые, по теореме умножения вероятностей для независимых событий будем иметь

.

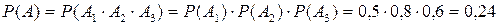б) Пусть событиеВ - нужная деталь содержится только в одном ящике. Это событие можно представить так:

,

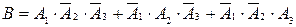где событие 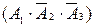означает, что нужная деталь содержится в первом ящике, а во втором и третьем ящиках нужной детали нет. Аналогично, событие 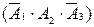- нужная деталь есть во втором, а в первом и третьем ящиках ее нет. Событие 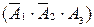- нужной детали нет в первом и во втором ящиках, в третьем она есть.

События, являющиеся слагаемыми последней суммы, несовместны, поэтому по теореме сложения вероятностей для несовместных событий получим

.

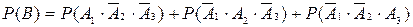Каждое слагаемое этой суммы можно найти, используя теорему умножения вероятностей для независимых событий

;

;

.

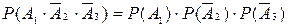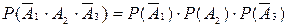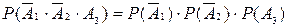Учитывая, что

;

;

,

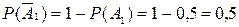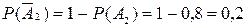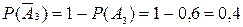окончательно получим

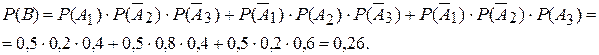
в) Пусть событиеС - нужная деталь содержится, по крайней мере, в одном ящике.

Рассмотрим противоположное событие 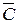- нужной детали нет ни в одном ящике, то есть 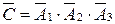. Тогда

.

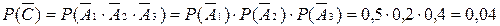Следовательно, .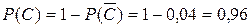

Задание 3. В сборочный цех завода поступили однотипные детали, изготовленные на трех автоматах. При этом с первого автомата поступило 600 деталей, со второго и третьего, соответственно, в 2 и 3 раза меньше. Известно, что первый автомат дает 3% брака, второй - 1%, а третий - 2% брака. а) Найти вероятность попадания на сборку годной детали, если деталь отбирается случайным образом. б) Наугад взятая деталь из сборочного цеха оказалась годной. Какова вероятность того, что она изготовлена на втором автомате?

Литература: 1, гл. 2. С. 23-26.

2, гл. 1. С. 26-28.

Решение. Пусть событиеВ - взятая наугад деталь оказалась годной. Это событие может произойти только вместе с одним из трех событий-гипотез:

событие 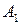- деталь изготовлена на первом автомате;

событие 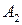- деталь изготовлена на втором автомате;

событие 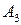- деталь изготовлена на третьем автомате.

События 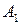, , 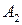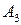образуют полную группу событий. Из условия задачи ясно, что на первом автомате изготовлено 600 деталей, на втором -300, а на третьем - 200 деталей. Отсюда находим

;

;

.

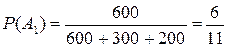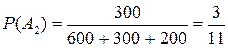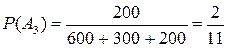В условии задачи даны условные вероятности события 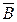(наугад взятая деталь бракованная), противоположного событиюВ, при гипотезах 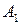, 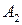и :

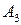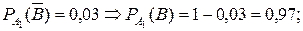
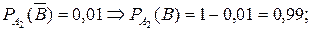
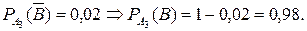
а) Вероятность событияВ найдем по формуле полной вероятности

.

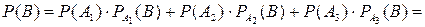
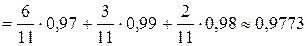б) Наугад взятая деталь оказалась годной, то есть событиеВ наступило. Вероятность того, что эта деталь изготовлена на втором автомате, вычисляем по формуле Байеса:

.

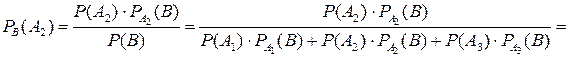
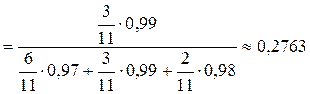Задание 4. Станок-автомат производит валики, причем контролируется размер их диаметра Х. Считая, что Х - нормально распределенная случайная величина с математическим ожиданием, равным 10 мм, и дисперсией, равной 0,01 мм²; найти: а) вероятность того, что размер диаметра валика будет от 9,8 до 10,3 мм; б) интервал, в который с вероятностью 0,9973 попадает размер диаметра наугад взятого валика.

Литература: 1, гл. 5. С. 81-95.

2, гл. 2. С. 78-80.

Решение. Диаметр валика - случайная величина Х, имеющая нормальный закон распределения со следующими параметрами:

; .

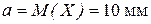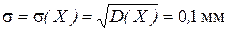а) Для нахождения искомой вероятности воспользуемся формулой

,

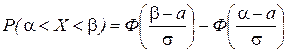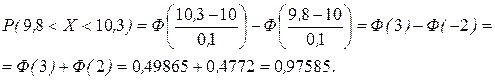
Здесь значения функции Лапласа Ф(3) и Ф(2) найдены по прил. 2.

б) Найдем искомый интервал с помощью формулы

.

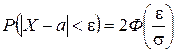Учитывая, что неравенство 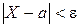равносильно неравенству 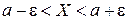, получим .

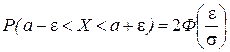По условию эта вероятность равна 0,9973, следовательно:

.

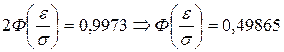По таблице значений функции Лапласа (прил. 2) находим 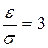. Отсюда, 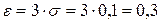. Таким образом, 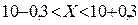или 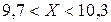. Искомый интервал - (9,7; 10,3) мм.

Задание 5. На ферме по схеме случайного повторного отбора были отобраны 100 коров. Распределение их по дневному надою (Х, л) следующее:

Дневной надой, л
Число коров

Вычислить выборочные характеристики: средний надой, моду, медиану, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.

Литература: 1, гл. 7. С. 125-130.

2, гл. 4. С. 110-114.

Решение. Признак Х - дневной надой коров. Для расчета выборочных характеристик данного распределения удобнее использовать таблицу:

Дневной надой (хi, л)	Число коров (mi)	хimi	Н(хi)	(х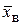i- )2mi	хi2mi
				63,48 54,08 18,72 58,80 80,92
Итого			-	276,00

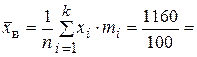11,6 (л) - средний дневной надой коров данной фермы.

Легко убедиться, что в случае дискретного признака Х в ранжированном вариационном ряду x_j=x_i при Н(х_i)+1£j£Н(х_i+1). Для рассматриваемого примера:x_j= 11 при 12£j£63.

Объем выборки n=100 - число четное. Пусть n=2j, тогда j=50. Поэтому медиана

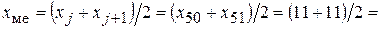11 (л).

Частота достигает максимума: m_i = m_max = 52 приx_i= 11, поэтому мода

х_мо= 11 (л).

Очевидно, х_мo=х_ме¹ 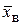. Таким образом, распределение признака Х асимметричное.

Размах вариации R = х_max - х_min= 15 - 7 = 8 (л).

Дисперсию можно вычислить двумя способами:

1)

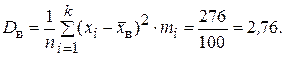
2)

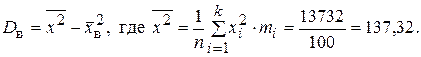
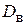= 137,32 - (11,6)² = 2,76.

Среднее квадратическое отклонение 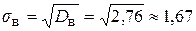(л) (дневной надой каждой коровы данной фермы отклоняется от среднего дневного надоя коров в среднем на 1,67 л).

Коэффициент вариации 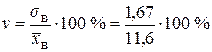»14,32 %.

На практике считают, что если 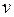<33%, то совокупность однородная. В данном случае исследуемая совокупность однородная.

Замечание. Если в условии задан интервальный ряд распределения признака Х, то сначала необходимо перейти к дискретному ряду, заменив интервалы их серединами.

Задание 6а. Установить при уровне значимости 0,05, случайно или значимо расхождение между эмпирическими и теоретическими частотами, которые вычислены, исходя из предположения, что некоторый признак Х распределен нормально:

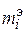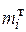Литература:1,гл. 9. С. 148-160.

2,гл. 5. С. 135-145.

Решение. Выдвигаем нулевую гипотезу Н₀ и ей конкурирующую Н₁.

Н₀: признак Х имеет нормальный закон распределения.

Н₁: признак Химеет закон распределения, отличный от нормального.

В данном случае рассматривается правосторонняя критическая область. Проверим гипотезу с помощью случайной величины 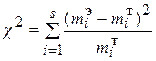, которая имеет распределение c² с k=s-3=7-3=4 степенями свободы. Вычислим наблюдаемое значение критерия c² по выборочным данным. Расчеты представим в таблице:

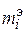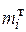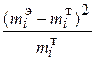			1,78 1,64 0,13 1,33 0,25 12,25 0,33
Итого			17,71

Итак, 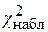»17,71. По прил. 3 находим критическое значение 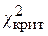(0,05; 4)=9,5. Сравниваем 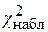и 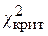(0,05;4).

Так как 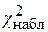> 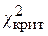(0,05; 4), то есть наблюдаемое значение критерия попало в критическую область, нулевая гипотеза отвергается, справедлива конкурирующая гипотеза, то есть признак Х имеет закон распределения, отличный от нормального, расхождение между эмпирическими и теоретическими частотами значимо.

Задание 6б. На предприятии разработаны два метода изготовления определенной продукции. Для проверки - одинаково ли материалоемки эти методы - собраны статистические данные о расходе сырья в расчете на единицу готовой продукции в процессе работы обоими методами. Получены следующие данные. При работе первым методом: количество наблюдений n_x=9, среднее значение 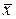_в=3,8, исправленное среднее квадратическое отклонение S_x=0,6; при работе вторым методом: количество наблюдений n_y=8, среднее значение
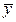_в=2,7, исправленное среднее квадратическое отклонение S_y=0,5. Согласно имеющимся данным проверить гипотезу о том, что средний удельный расход сырья при работе обоими методами одинаков, считая, что выборки извлечены из нормально распределенных генеральных совокупностей. Уровень значимости a=0,05.

Литература: 1, гл. 9. С. 161-172.

2, гл. 5. С. 152-155, 158-163.

Решение. Даны совокупности Х и Y, имеющие нормальный закон распределения, где Х - расход сырья при работе первым методом, Y - расход сырья при работе вторым методом. Требуется проверить гипотезу: Н₀:М(Х)=М(Y).

Так как о генеральных дисперсиях ничего неизвестно, то с помощью случайной величины 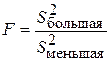, которая имеет распределение Фишера - Снедекора с k₁ =n_х-1=8 и k₂ =n_y-1=7 степенями свободы (n₁=n_х, так как 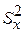= (0,6)² = 0,36, больше чем 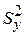= (0,5)² = 0,25) предварительно проверим вспомогательную нулевую гипотезу:

Н₀:D(Х)=D(Y) при Н₁:D(Х)>D(Y).

Находим F_набл= 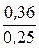=1,44. По прил. 5 определим критическое значение F_крит(a, k₁, k₂)=F_крит(0,05; 8; 7)=3,73.

Сравниваем F_набл и F_крит(0,05; 8; 7). Так как F_набл<F_крит(0,05; 8; 7), то есть F_набл попало в область принятия гипотезы, нет оснований отвергать нулевую гипотезу, по данным наблюдения D(Х)=D(Y), расхождение между исправленными выборочными дисперсиям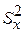и ( и 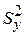) случайное. Следовательно, можно проверить основную гипотезу.

Предварительно выбираем конкурирующую гипотезу. В данном случае их может быть две: 1) Н₁:М(Х)¹М(Y) (двусторонняя критическая область); 2) Н₁:М(Х)>М(Y), так как 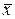_в> 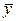_в (правосторонняя критическая область).

Проверяем гипотезу Н₀в первом случае:

Н₀: М(Х)=М(Y), Н₁: М(Х)¹М(Y).

Для проверки используется случайная величина

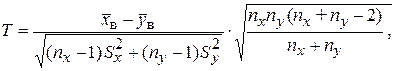
которая имеет распределение Стьюдента с k=n_x+n_y-2=9+8-2=15 степенями свободы.

Вычислим Т_набл 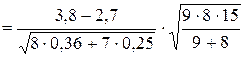» 4,075.

По таблице критических точек распределения Стьюдента (прил. 4) находим t_{крит.дв}(0,05;15)=2,13 (при двусторонней критической области). Сравниваем Т_набл и t_{крит.дв}(0,05;15). Так как ½Т_набл½>t_{крит.дв}(0,05;15), то есть Т_набл попало в критическую область, нулевая гипотеза отвергается, справедлива конкурирующая: М(Х)¹М(Y), следовательно, расхождение между выборочными средними значимо. Таким образом, средний удельный расход сырья при работе обоими методами различен.

Проверим гипотезу Н₀ во втором случае:

Н₀: М(Х)=М(Y), Н₁: М(Х)>М(Y).

Так как Т_набл»4,075, t_{крит.пр}(0,05;15)=1,75 (при односторонней (правосторонней) критической области), то Т_набл>t_{крит.пр}(0,05;15), то есть Т_набл попало в критическую область, вывод аналогичен предыдущему.

Замечание. В контрольную работу входит либо задание 6а, либо задание 6б (см. свой вариант).

Задание 7. В результате исследования зависимости выпуска валовой продукции (Y,тыс.руб.) от основных фондов (Х, тыс.руб.) однотипных предприятий получены следующие данные:

Х
Y

Полагая, что между Х и Y имеет место линейная зависимость, определить выборочный коэффициент корреляции, объяснить его смысл, проверить значимость коэффициента корреляции при уровне значимости 0,05. Построить уравнение регрессии и объяснить его. Вычислить предполагаемый выпуск валовой продукции, если основные фонды составят 80 тыс. руб.

Литература: 1, гл. 10. С. 182-196.

2, гл. 6. С. 177-182.

Решение. Признак Х-основные фонды, тыс.руб. (факторный признак). Признак Y-выпуск валовой продукции, тыс. руб. (результативный признак). Предполагаем, что признаки имеют нормальный закон распределения. Признаки находятся в статистической зависимости, так как выпуск валовой продукции зависит не только от основных фондов, но и от многих других факторов, которые в данном случае не учитываются. Определим форму связи. Построим точки с координатами (х_i, y_i) и по их расположению определим форму связи (см. рисунок).

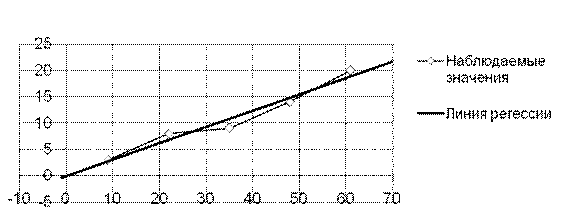
Рис.

Итак, форма связи линейная.

Проведем корреляционный анализ. Вычислим выборочный линейный коэффициент корреляции:

.

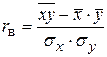Расчеты представим в таблице:

	хi	yi	хi×yi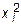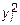
Итого