Теорема о сходимости к стационарному распределению
Пусть существует хотя бы одно состояние 
и такие 
и 
, что 
. Тогда существует и притом единственное стационарное распределение 
, такое, что 
при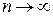 
. Кроме того, 
равномерно по всем состояниям не зависимо от начального распределения вероятностей.
Пример 2.1. В моменты времени 
производится осмотр ЭВМ. Возможные состояния ЭВМ: 
– полностью исправна; 
– незначительные неисправности, которые позволяют эксплуатировать ЭВМ; 
– существенные неисправности, дающие возможность решать ограниченное число задач; 
– ЭВМ полностью вышла из строя. Матрица переходных вероятностей имеет вид:
.
Построить граф состояний. Найти вероятности состояний ЭВМ после трех осмотров, если вначале (при 
) ЭВМ была полностью исправна.
Решение. 
По условию вектор вероятности состояний ЭВМ в начальный момент времени (до первого осмотра) равен
.
После трех осмотров он будет равен 
,
где 
, 
, 
.
С вычислительной точки зрения данную задачу проще решать по рекуррентной формуле:
, 
,
, 
,
.