Вычисление обратных матриц второго и третьего порядков
Для нахождения обратной матрицы используют следующую схему:
1°. Находят определитель матрицы А.
2°. Находят алгебраические дополнения всех элементов аij матрицы А и записывают новую матрицу.
3°. Меняют местами столбцы полученной матрицы (транспонируют матрицу).
4°. Умножают полученную матрицу на 1/D.
1. Найти матрицу, обратную матрице А = 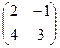 . Р е ш е н и е. 10. Находим определитель матрицы А: D = . Р е ш е н и е. 10. Находим определитель матрицы А: D = 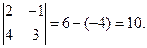 Так как D ≠ 0, то данная матрица является невырожденной и, следовательно, существует обратная матрица. 20. Найдем алгебраические дополнения каждого элемента данной матрицы: А11 = (-1)1+1 · 3 = 3; А12 = (-1)1+2 · 4 = -4; А21 = (-1)2+1 · (-1) = 1; А22 = (-1)2+2 · 2 = 2. Тогда получим матрицу Так как D ≠ 0, то данная матрица является невырожденной и, следовательно, существует обратная матрица. 20. Найдем алгебраические дополнения каждого элемента данной матрицы: А11 = (-1)1+1 · 3 = 3; А12 = (-1)1+2 · 4 = -4; А21 = (-1)2+1 · (-1) = 1; А22 = (-1)2+2 · 2 = 2. Тогда получим матрицу 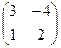 . 30. Транспонируем эту матрицу: . 30. Транспонируем эту матрицу: 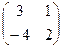 . 40. Умножим полученную матрицу на 1/D, т.е. 1/10: А-1 = . 40. Умножим полученную матрицу на 1/D, т.е. 1/10: А-1 = 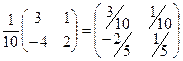 . Проверим полученный ответ. Выполнив умножение АА-1, находим . Проверим полученный ответ. Выполнив умножение АА-1, находим 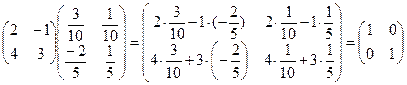 = Е. = Е. |
