События называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании.

Введение.

В жизни часто приходится иметь дело с явлениями, носящими случайный характер. Выполнение определенного комплекса условий будем называть опытом (экспериментом), а результат опыта – событием. Простейший пример – подбрасывают монету. Выпадение герба или цифры – случайные события, но при довольно большом количестве повторений опыта в одинаковых условиях можно заметить, что появление герба происходит примерно в половине случаев. Таким образом, в мире случайностей обнаруживаются определенные закономерности. Математический аппарат для изучения массовых однородных случайных явлений дает теория вероятностей.

Раздел математики, изучающий закономерности случайных событий, называют теорией вероятностей.

События материального мира можно разделить на три категории: достоверные, невозможные и случайные.

1. Достоверным называется событие, которое в данном опыте обязательно должно произойти. Например, таким событием является падение монеты при ее подбрасывании монеты.

2. Невозможным называется событие, которое в данном опыте не может произойти. Например, при подбрасывании монеты она не падает.

3. Случайным называется событие, которое в данном опыте может произойти или не произойти. Например, таким событием является выпадение «герба» или «цифры» при подбрасывании монеты.

Для каждого события А можно определить вероятность этого события p(A), представляющее «меру достоверности» данного события и подчиненное естественным требованиям. Вероятность любого события удовлетворяет неравенству: 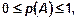причем вероятность невозможного события равна нулю, а вероятность достоверного события равна единице.

В создании теории вероятностей участвовали многие крупные математики: Паскаль, Ферма, Лаплас, Гаусс, Пуассон и др. В более поздний период решающие успехи в этой науке принадлежат российским математикам: Чебышеву, Маркову, Ляпунову, Бернштейну, Колмогорову, Хинчину и др.

Основные определения.

События называются равновозможными, если объективно по условиям симметрии ни одно из них не является более возможным, чем другие.

Примеры:

1. Появление цифры или герба при бросании монеты – события равновозможные, если монета изготовлена из однородного материала, имеет правильную цилиндрическую форму и наличие чеканки не оказывает влияния на выпадение той или другой стороны монеты. Если же монета, к примеру, погнута, то выпадение одной ее стороны становится более возможным.

2. Появление того или иного числа очков при бросании игральной кости – события равновозможные, если кость изготовлена из однородного материала, имеет форму правильного многогранника и наличие очков не оказывает влияния на выпадение той или другой грани.

События называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании.

Примеры:

1. Из ящика с деталями наудачу извлечена одна деталь. Появление стандартной детали исключает появление нестандартной детали. События – появление стандартной детали и появление нестандартной детали – события несовместные.

2. Попадание в цель и промах при одном выстреле – события несовместные.

3. Пусть А – появление четырех очков при бросании игральной кости; В – появление четного числа очков при бросании игральной кости. Число 4 является четным. События А и В – совместные.