Лінійні диференціальні рівняння вищих порядків

I. ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ -ГО ПОРЯДКУ

В загальному випадку диференціальне рівняння -го порядку, яке можна розв’язати відносно старшої похідної, має вид

Загальним розв’язком (інтегралом) диференціального рівняння називається функція

яка залежить від довільних сталих і задовольняє двом умовам:

1) при довільних значеннях сталих перетворює в рівняння тотожність;

2) при довільних початкових умовах

існують такі значення сталих , при яких функція задовольняє цим умовам.

Для задачі Коші і є теорема про існування та єдність розв’язку.

Якщо функція неперервна в області D разом зі своїми частинними похідними , ,..., , тоді для будь якої точки (х₀,у₀), яка належить області D, задача Коші має і причому єдиний розв’язок, визначений в деякому околі точки х_0.

ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ, ЯКІ ДОПУСКАЮТЬ ЗНИЖЕННЯ ПОРЯДКУ

1) рівняння виду

Розв’язок даного рівняння знаходиться -кратним послідовним інтегруванням. Так як , то дане рівняння може бути переписане у вигляді: , або

Інтегруючи послідовно рівняння, одержимо

.

(1.1)

Аналогічно, інтегруючи вираз (1.1), знаходимо

і так далі.

Загальний розв’язок матиме довільних сталих ; для одержання частинного розв’язку необхідно використовувати початкові умови (2).

Приклади.

1. Знайти загальний розв’язок .

Найдемо загальний розв’язок рівняння послідовним інтегруванням даного рівняння:

Тоді - загальний розв’язок.

2. Розв’язати задачу Коші

Найдемо загальний розв’язок рівняння послідовним інтегруванням даного рівняння:

- загальний розв’язок.

Знайдемо значення сталих , які задовольняють заданим початковим умовам:

Частинний розв’язок матиме вид

.

2) рівняння виду

Порядок такого рівняння можна понизити за допомогою заміни , тоді і так далі.

Визначаємо загальний розв’язок для функції з рівняння у вигляді .

Далі, після інтегрування співвідношення , маємо загальний розв’язок початкового рівняння:

.

Приклад. Знайти загальний розв’язок рівняння

Рівняння не має явно початкової функції , отже, використовуємо заміну

, .

Підставляючи вираз для 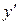і 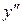в дане рівняння, одержимо рівняння першого порядку відносно функції :

Одержане рівняння є рівнянням з відокремлюваними змінними:

Так як , то

- розв’язок рівняння.

3) рівняння виду

Тут немає 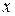. Порядок такого рівняння можна понизити за допомогою заміни , тоді .

В результаті порядок початкового рівняння понижується на одиницю:

.

Якщо знайдено розв’язок для функції

, то одержимо

або

- рівняння відокремлюваними змінними відносно змінних 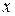і .

Приклад. Знайти загальний інтеграл рівняння

.

Дане рівняння не має незалежної змінної 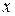.Робимо заміну

, .

Підставляючи вираз для 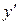і 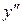в дане рівняння маємо:

Одержане рівняння є рівнянням з відокремлюваними змінними:

Так як ,

Загальний інтеграл має вид:

,

,

.

ЛІНІЙНІ ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ВИЩИХ ПОРЯДКІВ

Лінійне диференціальне рівняння -го порядку в загальному випадку має вид

(2.1)

де - задані неперервні функції.

Якщо , то рівняння (2.1) називають лінійним однорідним диференційним рівнянням -го порядку.

Загальний розв’язок лінійного однорідного диференційного рівняння -го порядку визначається як лінійна комбінація його лінійно незалежних частинних розв’язків, тобто

,

де 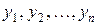- лінійно незалежні частинні розв’язки лінійного однорідного рівняння ; - довільні сталі.

Систему функцій 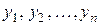називають лінійно незалежною на (а,b ), якщо тотожність

,

виконується тільки при С_і=0, у противному разі система лінійно залежна.

Для того щоб розв’язки 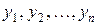лінійного однорідного диференційного рівняння були лінійно незалежними на (а,b ),необхідно і достатньо, щоб визначник , для будь якого . Цей визначник позначають W(x) і називають детермінант Вронського.

Для двох функцій можна дати більш простий критерій лінійної незалежності.

Функції лінійно незалежні, якщо їх відношення тотожно не дорівнює сталій величині , якщо , то функції лінійно залежні.

Загальний розв’язок рівняння (2.4) 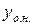може бути представлений у вигляді суми загального розв’язку відповідного однорідного рівняння і деякого частинного розв’язку неоднорідного рівняння , тобто

.
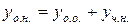