Задача Коши для дифференциального уравнения и для системы дифференциальных уравнений. Теоремы существования и единственности решения. Случай линейных уравнений и систем. 3 страница

33.Интуитивное понятие алг-ма.Машина Тьюринга.Тезис Черча.Интуитивное понятие алг-ма. Прежде чем дать строгое матем-кое опр-е понятия алг-м рассм-им осн. его св-ва:1)Массовость–алг-м пригоден для реш-я не 1-ой з-чи,а целого класса однотипных з-ч.2)Дискретность–алг-м раб-ет в дискретном времени так,что в исходный момент времени задается начальный набор величин,а в каждый последующий–набор величин получ.из набора им-гося в предыдущий момент времени.3)Детерминированность–действия,выполн-ся на каждом этапе опр-ся однозначно и однозначно опр-ся переход к следующему этапу.4)Элементарность шагов алг-ма-действия,выполн-ся на каждом этапе д.б.достаточно простыми.5)Направленность шагов алг-ма-если в рез-те выполнения какого-то этапа мы получим рез-т,то д.б.указано,что следует принимать за рез-т.Эти св-ва в какой-то степени опр-ют понятие алг-м.Такое понятие наз.интуитивным.Рассмотрим строгое матем-ое опр-ие понятия алг-м.Тьюринг исходили из того,что алг-ский процесс-процесс,кот.может выполнять устроенная подходящим образом“машина”.Он описал такие машины и в последствии эти машины были названы машинами Тьюринга.МТ состоит из ленты и головки.Лента ∞ в обе стороны,разделена на ячейки равной длины. В каждой ячейке записан ровно 1 символ из мн-ва {а₀,а₁,...,а_n}наз.внешним алфавитом МТ.В каждый момент времени головка находиться у вполне опр-ой ячейки.В каждый момент времени головка нах-ся в одном из состояний мн-ва {q₁,q₂,…,q_n}наз-го внутренним алфавитом МТ.В зависимости от того,в каком состоянии нах-ся головка и какую ячейку она обозревает головка выполняет следующие действия:1)стирает записанный в обозреваемой ячейке символ и записывает туда новый.2)сдвигает влево (Л),вправо(П) к соседней ячейке или остается на месте(С).3)переходит в новое внутр. состояние или остается в том же.Выполнение этих действий наз.выполнением команды, а сама команда записывается в виде:q_ia_i→a_jD_jq_j,где q_i–состояние головки в данный момент,a_i–символ в обозреваемой ячейке,a_j-символ запис-ый в обозреваемую ячейку,D_j 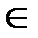{Л,П,С},q_j-состояние,в кот.переходит головка.Совокупность всех команд наз.программой МТ.Состояния q₁и q₀ наз.соответственно начальным и конечным. Конфигурацией МТ наз.совокупность след.3-х усл-ий:1)слово на ленте(последовательность символов в ячейках ленты);2)указание обозреваемого символа;3)состояние головки.В зависимости от пр-мы МТ и нач-ой конфигурации м.б.2 случая:1.после конечного числа раз выполнения команд машина приходит в состояние q₀,после чего она останавливается в том случае рез-ом работы машины счит-ся конечная конфиг-ия;2.головка машины никогда не приводит в состояние q₀.В этом случае машина раб-ет ∞ и говорят,что машина не применима к начальной конфиг-ии.Ф-ия наз.числовой,если она сама и её арг-ты принимают знач-я из мн-ва {0,1,2,3…}.Числовая ф-ия f(x₁,x₂,…,x_n)наз.вычислимой по Тьюрингуили просто вычислимой ф-ей,если им-ся такая МТ,что выполняется 2 усл-я:1)если f(m₁,m₂,..,m_n)=m,то машина слово на ленте 1^m1+1 0 1^m2+1 0 … 1^mn+1преобразует в слово 1^m+1;2)если знач-е f(m₁,m₂,..,m_n) не опр-но,то машина не применима к слову 1^m1+1 0 1^m2+1 0 … 1^mn+1.Тезис Чёрча: Всякий алг-м м.б.задан пр-мой МТ.Уверенность в справедливости ТЧ базируется на опыте.Опыт подсказывает,что не было ещё ни одной успешной попытки создания такого алг-ма,кот.невозможно было бы задать пр-мой МТ.Еще одним важным доводом явл-ся также эквивалентность различных строгих опр-ий понятия алг-м.А это говорит о том,что все эти различные строгие опр-я верно отражают природу алгоритма.

34.Исчисление высказываний.В логике при исследовании высказываний для выяснения того является ли данная ф-ла выполнимой(если на мн-ве М им.хотябы 1-н набор знач-й перемен-х из М, на кот.ф-ла приним.знач-е истина)или равносильны ли две данные ф-лы(если на любом наборе знач-й перемен.из М эти ф-лы приним.одинак.истинное знач-е)достаточно было построить таблицу истинности.Это было возможно,т.к.каждая перемен-я явл.лишь двоичной.В др.разделах такой метод не подходит т.к.переменные могут принимать сколь угодно много различ.знач-й.В таких случаях примен-ся так называемый аксиоматический метод.Рассмотрим применение этого метода в наиболее простом случае при исследовании высказываний.Аксиоматическую теорию,кот.в рез-те этого построим,наз-ем исчислением высказываний(ИВ).Каждой аксиоматической теории свойственны 3 след-ие черты:1)Язык включ.в себя алфавит и способы образования ф-ул.Опр.Алфавитом ИВ наз.мн-во,состоящее из 3-х групп символов:-большие печатные буквы латинского алфавита с индексами или без них (А,В₁,С₃…);-спец.символы“→”,“—”;-скобки (, ).Способы образования ф-ул–это те правила,по кот.из символов данного алфавита строят ф-лы. В ИВ явл-ся таким след-ие правила:1)каждый символ 1-ой группы алфавита является ф-лой;2)если А–ф-ла,то 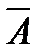–тоже ф-ла;3)если А и В –ф-лы,то(А→В)ф-ла;4)др.ф-ул нет.В опр-ии ф-лы использовали символы А и В 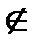алфавиту.Такие символы называются метасимволами.2)Аксиомы:во мн-ве ф-ул каждой аксиоматической теории выделяют некоторое подмн-во,ф-лы кот.и объявляют аксиомами. В ИВ все аксиомы задаются с помощью след-их 3-х схем: 1.А→(B→A); 2.(A→(B→C))→((A→B)→(A→C));3.(B¯ →A¯ )→((B¯ →A)→B).Эти 3 схемы порождают ∞ мн-во аксиом,кот.получаются при подстановке конкретных ф-ул на место метасимволов.3)Правила вывода:они позволяю из им-ся ф-ул получать новые.При этом те ф-лы,к кот.применяются правила вывода наз.посылками,а та ф-ла, кот. получается заключением.В ИВ им-ся всего одно правило вывода: modus ponens(MP). Это правило будучи примененным к ф-ле вида A и A→B дает ф-лу B.

Выводомназ.конечная послед-сть ф-ул,в кот.каждая ф-ла получена по одной из схем аксиом или по правилу вывода из предшествующих ф-ул.Ф-ла наз.выводимой,если им.вывод,в кот.эта ф-ла нах-ся на последнем месте.Если ф-ла В выводима,то пишут├В.Пусть дано некоторое мн-воф-ул Г,формулы этого мн-ва наз-ём исходными или гипотезами.Тогда выводом ф-лы В из гипотез Г наз.конечная посл-ть ф-л,в кот.на последнем месте нах-ся ф-ла В и в кот.каждая ф-ла получена либо по схеме аксиом, либо по правилу МР из предшествуюших,либо явл.гипотезой.Пишут Г├ В. Т.дедукции.Если из Г,А├В,то из Г├А→В.Аксиоматическая теория наз. непротиворечивой,если в ней из каждой пары ф-ул вида В и B¯ невыводимой явл хотя бы одна.ИВ наз.полным в широком смысле,если в нем выводимы все ф-лы,кот.в логике высказываний явл.тавтологиями(тавтология–при любом наборе истинностных знач-ий,вход-х в нее букв приним.знач.1,по-другому закон логики).ИВ назыв полным в узком смысле,если присоединив к его схемам аксиом любую невыводимую ф-лу мы получим противоречивую теорию.ИВ наз.абсолютно полным,если в нем из каждой пары ф-ул вида В и B¯ выводимой явл. хотя бы одна.Схема аксиом наз.независимой, если не одну из схем аксиом нельзя вывести из остальных.

35.Метод обратной функции моделирования непрерывной случайной величины.Моделирование на ЭВМ случайного элемента подчиняется двум основным принципам: 1) сходство между случайным элементом-оригиналом S* и его моделью S состоит в совпадении (близости) вероятностных законов распределения или числовых характеристик; 2) всякий случайный элемент S определяется как некоторая функция от простейших случайных элементов, так называемых базовых случайных величин

(БСВ). В качестве БСВ выбирается непрерывная случайная величина(СВ) α равномерно распределенная на полуинтервале [0, 1).

Функция распределения БСВ: 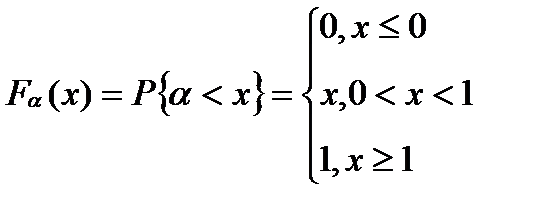(1),а плотность распределения определяется формулой: 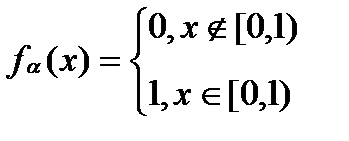.Если возникает необходимость моделирования непрерывной СВ ξ* с за-

данной плотностью распределения f (x), то в некоторых случаях для решения данных задач удается применить метод обратной функции. Функция распределения СВ ξ* определяется как: 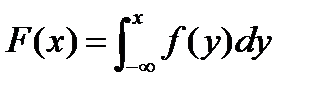(2),кот.будем полагать строго монотонно возрастающей. Через x = F 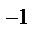(y) обозначим обратную функцию; она находится при решении уравнения F(x) = y . (3) Теорема. Если α — БСВ, то СВ ξ=F 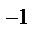(α) (4)им.заданную плотность распределения f (x).Док-во. Поскольку при строго монотонном преобразовании F(x) знак неравенства сохраняется, то из (3) и (2) получаем: Fξ(x) =[По определению ф-ии распределения]=P(ξ<x)=[ По формуле (4)]=P(F 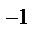(α)<x)=[По свойству монотонности ф-ии распределения]= =P(α<F(x))=[ По определ.ф-ии распределения]=F 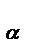(F(x))=[ По формуле (1)]=F(x) т.е. F 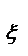(x) =F( x),а с учетом (2) получаем что f 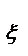(x)=f( x),.

Моделирующий алгоритм включает следующие этапы: 1) нахождение ф-ии распределения F(x) по заданной плотности распределения f (x) согласно (2); 2) нахождение обратной ф-ии F 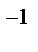(y) путем решения уравнения (3); 3) моделирование реализации БСВ α и вычисление реализации ξ по формуле (3).

Коэффициент использования БСВ κ = 1. Недостатком метода явл.аналитические трудности на первых двух этапах.В чистом виде метод обратной ф-ии применяется редко т.к.для многих распределений даже F(x) (не говоря уже о F 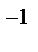(y)) не выражается ч/з элементарные ф-ии,а табулирование F 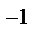(y) существенно усложняет моделирование.На практике этот метод дополняют аппроксимацией F(x) или сочетанием с другими методами.

36. Минимальные покрывающие деревья.Графом G=(V,E) наз. совокуп-ть непустых множ-в V и E, сост. из пар эл-ов множ-ва V. Если эл-ты мн-ва E явл. неупорядоченными, то они наз. рёбрами и граф-неориентир-ый, если упорядочены, то –дуги и граф ориентир-ый. Неориентир. граф наз. связным, если 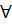его 2 вершины можно соед. путём. Путь-послед-ть рёбер, в кот. 2 сосед. ребра смежны(-им. общую концевую точку). Дерево – граф без циклов(-путь, в кот. 2 сосед. ребра смежны). Пусть дан связный неориентир. граф G=(V,E) и пусть каждому ребру припис. число >= 0 –вес ребра. Покрывающим(остовным)деревом связного неориентир. графа G=(V,E) наз. такой его подграф, кот.сод. все вершины исходного графа и явл. деревом. Min покрыв. деревом(МПД) связного неориентир. графа G=(V,E) наз.такое покрыв. дерево, кот. им. наименьшую сумму весов рёбер среди всех покрывающих деревьев. Рассм. 2 алгоритма построения МПД. Их общая схема: Выделяем нек-ое подмнож-во А, кот. будет частью МПД, затем к нему добавл. ребро 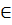МПД и оно наз. безопасным. Алгоритм Крускала.Идея: им. |V| мн-в, каждое из кот. сост. из 1 вершины. Каждая такая вершина образует дерево. Затем на каждом шаге доб. 1 ребро, с пом. кот. происходит объединение 2 деревьев в 1. Здесь исп. след. процедуры: 1) find_set (u)- возвращ. представит мн-ва, содержащего эл-т u, при этом 2 вершины u,v 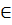одному мн-ву, если вып. find_set (u)= find_set (v); 2) union (u,v)- объед. 2 мн-ва, представит-ми кот. явл. u,v; 3) make_set (u)- созд.мн-во, ед. эл-ом кот. и представителем явл. u;

Mst_Kruskal(G,l):

1) А= 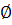2) for каждой v 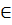V do make_set(v)

3) for (u,v) 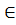E (в порядке возраст. веса) do if find_set(u) 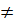find_set(v) then A:=A 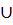{(u,v)} union(u,v) 4) return A

т.е. на каждом шаге берём ребро min веса. Если найденное ребро связывает 2 вершины из разных связных компонент графа А, то его добавляют в граф А, иначе это ребро отбрасывают т.к. его добавление в граф приведет к образованию цикла, и объед. мн-ва. O(|E|*log₂|E|)- время работы алгоритма.

Пр.

итер1 (1,3) вес 1; связанные компоненты {1,3}

итер2 (4,6) вес 2; связанные компоненты {1,3};{4,6}

итер3 (2,5) вес 3; связанные компоненты {1,3};{4,6};{2,5}

итер4 (3,6) вес 4; связанные компоненты {1,3,4,6};{2,5}

итер5 (3,4) нет т.к образуется цикл

(1,4) нет т.к образуется цикл

(2,3) вес 5; связанные компоненты {1,3,4,6,2,5}

Алгоритм Прима.Идея: в нач. выб. 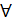вершина графа. r- корень дерева. Затем на кажд. этапе выб. ребро наименьшего веса, соед. вершины уже построенного дерева с вершиной не из дерева. В ходе работы алг-ма все вершины, ещё не попавшие в дерево, хранятся в очереди с приоритетами Q(мн-во, эл-ты кот. явл. числа). Приоритет вершины v в этой очереди опред. знач-ем key[v] и оно = весу наименьшего ребра, соед. вершину v c вершиной из дерева. Если такого ребра нет, то key[v]= 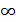. П[v] указ. на родителя вершины v в дереве. l(u,v)- вес ребра (u,v).

Mst_Prim(G,l,r):

1) Q:=V 2) for каждой вершины u 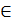Q do key[u]:= 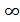3) key[r]:=0

4) П[r]:=null 5) while Q 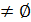do u:=extract_min(Q) 6)for каждой v 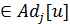do

if v 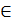Q and l(u,v) < key[v] then П[v]:=u; key[v]:=l(u,v) Здесь extract-min() –изъятие min эл-та из мн-ва. Время работы зав. от способа реализации очереди Q. (если Q двоичная куча, то время работы O(|E|*log₂|V|)

37. Оптимальные коды.Кодирование всегда играло существенную роль в матем-ке. Позволяет решать след.зад-чи: 1)представл. данных произвольной природы в памяти компа(чисел, текста, графики и т.д) 2)обеспеч. помехоустойчивости при передаче данных по каналам связи 3)защита инф-ции от несанкционированного доступа 4)сжатие инф-ции в базах данных. Пусть дан алфавит A={a₁, a₂,…a_n}, тогда конечные посл-ти A=a_i1a_i2…a_{i n} букв алфавита А наз. словом в алфавите А, при этом n- длина слова. Мн-во всех слов в алфавите А обознач. S(A), для алфавита В -S(B). S’(A )-подмн-во S(A) и его слова наз. сообщениями. Пусть дано отображение F, кот. каждому слову A 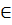S’(A) ставит в соотв. слово B 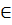S(B), B=F(A), тогда слово B наз. кодом слова А, а сам переход от слова А к В наз. кодированием. Основная з-ча теории кодирования – найти такое F при заданных алфавитах А и В и мн-ве сообщений S, кот. обладает опред. св-вами и оптимально в некотором смысле. Рассм. алфавитн. кодирование, при кот. каждой букве a_i 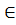A ставится в соотв. слово B_i 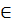B, т.е.

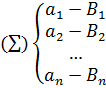и эта схема наз. схемой алфавитного кодирования. |B_i|= 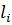- длина слова B_i Пусть даны вероятности p₁,p₂…p_n появления в сообщениях соотв. букв a₁, …a_n. Для определённости 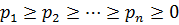. Очевидно 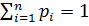. Ценой или длиной алфавитного кодирования ∑ при данном распределении P=( p₁,p₂…p_n) наз. величина 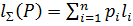. Цена кодирования означает матем. ожидание коэффиц. увеличения длины сообщения. Алфавитное кодирование 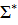, для кот. вып. усл-е 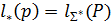наз. алфавитным кодированием с min избыточностью или оптимальным кодированием при данном распределении вероятности P, где 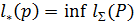Коды Хоффмана(строит оптимальный код).Суть алгоритма: находим буквы a_i, a_j алфавита А, кот. им. наименьшие вероятности. Затем эти 2 буквы заменяют новой буквой х, вер-ть кот. = сумме вер-тей букв a_i, a_j. После этого к алфавиту, у кот. кол-во букв уменьшилось на 1, применяем описанную процедуру и т.д. Для реализ. алг-ма Хоффмана исп. лес. В начале работы алгоритма лес сост. из n деревьев, кот. явл. вершины, соотв. буквам алфавита. Каждому такому дереву(вершине) приписана вероятность соотв. буквы. Замене букв a_i, a_j буквой x будет соотв. операция объединения 2-х деревьев в одно, при этом левым ребёнком в объед. дереве должна быть вершина с меньшей вероят-ю.

В алгоритме будет исп. очередь с приоритетами Q, в кот. хранятся символы алфавита А. Приоритет эл-та a_i в этой очереди опред. вер-ю p_i. Исп. процедура allocate_node() для выделения памяти, фун-ии :extract_min() – изъятие из мн-ва min эл-та, insert(Q, x)- добавление эл-та x ко мн-ву Q.

Huffman(A):

1) n:=|A| Q:=A 2) for i:=1 to n-1 do z:= allocate_node 3) x:=left[z]:=extract_min(Q)

y:=right[z]:=extract_min(Q) 4) P(Z):=p(x)+p(y) 5) insert(Q, z) 6) return extract_min(Q)

Время работы алгоритма O(n log₂n).

38.Выпуклое программирование. Теорема Куна –Таккера.Функция ¦(х), определенная на выпуклом множестве X, называется выпуклой(вогнутой), если для любых точек х' и x" из этого множества и любого 0£l£1 справедливо неравенство

¦(lx'+ (1 -l)х")£¦(х') +(1 -l)¦(x").М-во МÍХ назыв выпуклым, если любых a,b из М отрезок их соединяющий включается в М.

Задачи оптимизации (экстремальные задачи) - задачи вида: Задано векторное пространство X, функционал f: XàRÈ{+¥} и подмножество MÍX. Требуется найти минимальное значение функционала f на множестве M. При этом f называется целевым функционалом, множество X – основным пространством задачи, множество M задает ограничения задачи, его элементы называются допустимыми для задачи. Задачу оптимизации называют выпуклой, если целевой функционал f и ограничения M являются выпуклыми (соответственно, как функция и как множество).

Теорема 1 (Кун, Таккер). Пусть X – векторное пространство, fi:XàRÈ{+¥}, i=0,…,m – некоторые функционалы, AÍX. Предположим, что множество B={(b0, b1,…,bm)ÎRm+1| $xÎA: "i=0,..,m fi(x)£bi} – непустое и выпуклое. Тогда 1) Если x* – решение задачи 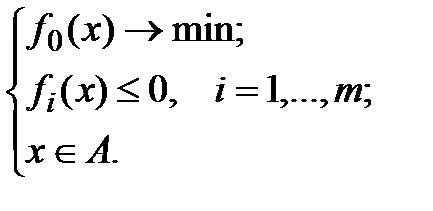(1) то найдется ненулевой вектор множителей Лагранжа l*=(l0*,…,lm*)ÎRm+1, такой что для функции Лагранжа L(x,l)= 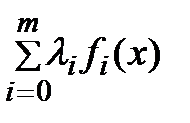выполняются следующие условия: а) принцип минимума для функции Лагранжа: 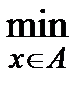L(x,l*)= L(x*,l*);(2) б) условие дополняющей нежесткости: l_i*f_i(x*) = 0, i=1,…,m; (3)

в) условие неотрицательности: li* ³ 0, i=0,…,m; (4)

2) Если l₀* > 0, то условия (2) - (4) достаточны для того, чтобы допустимая точка x* была решением задачи (1). 3) Для l₀* > 0 достаточно выполнения условия Слейтера: $x1ÎA: "i=1,…,m fi(x1) < 0. (5) Схема док-ва условий для мн-ей Лагранжа.

А) Пусть x* - решение задачи (1). Будем считать, что f₀(x*)=0 (заменим f₀(x) на f₀(x) - f₀(x*)). Пусть C = {(c0, 0,…,0)ÎRm+1| c0 < 0}. Мн-во C – непустое и выпуклое. Далее док-ваем от противного, что BÇC=Æ.Т к В и С не пусты и выпуклы и не пересеаются -> что существует не нулевой вектор 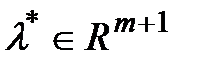для которого справедливо неравенство 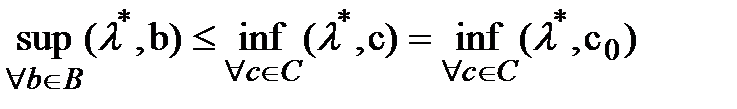Т.к ненулевой вектор тоже принадлежит В, получим 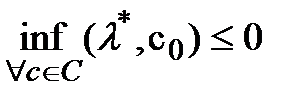а с другой стороны 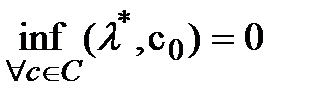т.к 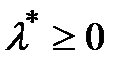Следво для всех bÎB выполняется условие 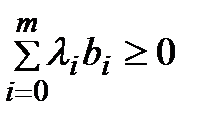(6). Аналогично если поменять местами B и С.

Г) Для каждого j=0,…,m вектор ej=(0,…,1,…,0) (1 на j+1-м месте) входит в множество B, поэтому его можно подставить в (6), из чего получаем условие неотрицательности (4).

Д) Зафиксируем i. Если fi(x*) = 0, то li*fi(x*)=0. Предположим, что fi(x*) ¹ 0, т.е. fi(x*) < 0. Тогда вектор b=(0,…, fi(x*),…,0) ÎB. Подставляя его в (6), получаем неравенство li*fi(x*)³ 0. Однако с учетом того, что fi(x*) < 0, li*³ 0, получаем, что li*= 0, а значит, снова li*fi(x*)=0. Условие (3) доказано.

Е) Пусть xÎA. Тогда вектор b=( f0(x),…, fi(x),…, fm(x)) ÎB. Подставляя его в (6), получаем: 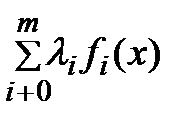= L(x,l*) ³ 0. С учетом усл-я дополняющей нежесткости получаем, что L(x*,l*)= 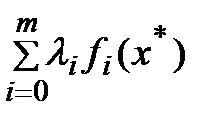=0., т.е для всех xÎA выполняется неравенство L(x,l*) ³ 0 = L(x*,l*), которое означает выполнение принципа минимума (2).

Пусть F=F(x,l) – функция двух переменных, определенная для всех xÎQÍX и всех lÎMÍRm+1. Точка (x*,l*), x*ÎQ, l*ÎM называется седловой для функции F, если для всех xÎQ и всех lÎM, выполняется неравенство: F(x*, l) £ F(x*, l*) £ F(x, l*).

С помощью понятия седловой точки можно сформулировать теорему Куна-Таккера: Теорема 2. Рассмотрим выпуклую задачу (1), для которой выполнено условие Слейтера (5).

1) Если x*- допустимый вектор, l*³0 (l*0=1) и (x*,l*) – седловая точка для функции Лагранжа L(x,l)= 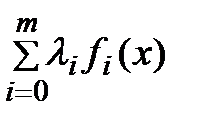на множестве допустимых векторов x и l³0 (l0=1), то x*- решение задачи (1).

2) Пусть x*- решение задачи (1). Тогда найдется вектор l*³0, такой что пара (x*,l*) – седловая точка для функции Лагранжа L(x,l) на множестве допустимых векторов x и l³0 (l0=1). В обоих случаях выполняются условия дополняющей нежесткости (3).

39.Давление идеального газа. 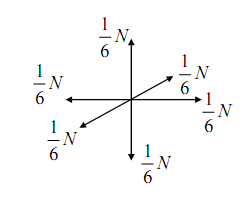Природа давления газа. Оценка давления газа для случая, когда скорости всех молекул одинаковы и направления движения строго определены относительно стенок сосуда. Оценка давления газа для общего случая. Связь давления и средней кинетической энергии молекул. Давление газа на стенку сосуда есть результат ударов молекул газа о стенку этого сосуда. Рассмотрим систему, состоящую из очень большого числа атомов или молекул, считая их маленькими, не взаимодействующими между собой шариками. Пусть вследствие малости объемов молекул по сравнению с объемом сосуда, в который они заключены, большую часть времени любая молекула находится в движении, относительно редко сталкиваясь с другими молекулами. Столкновения молекул газа со стенками, как показывает опыт, вызывают её упругое отражение. За давление газа принимают величину P = F/S , определяемую, как отношение силы, действующей на участок стенки сосуда со стороны ударяющих молекул к площади этого участка, усредненную за очень большие по сравнению с длительностью удара и длительностью промежутка времени между двумя последовательными ударами промежутки времени.

Установим количественную характеристику давления, применив упрощенный подход. Очевидно, что в однородном изотропном пространстве любые направления движения молекул равновероятны. Как следствие, в трехмерном пространстве в направлении избранной оси движется 1/3 N молекул, если N — полное число молекул, находящихся в рассматриваемом объеме. Если считать, что половина молекул движется «вдоль» оси, другая половина – «против», то в выделенном направлении будет двигаться 1/6 от общего числа молекул. Сделаем предельно упрощающее задачу приближение: все молекулы, содержащиеся в объеме, обладают одинаковой по модулю скоростью v.