Задача №1. Расчет ступенчатого бруса на прочность при растяжении
На составной ступенчатый брус, схема которого представлена на рисунке 2.4, действует система сил.
Ступени бруса изготовлены из различных материалов: Ма1 – бронза, Ма2 – сталь, Ма3 – чугун.
Рисунок 2.4 - Схема ступенчатого бруса
Требуется:
¾ построить эпюры продольных сил,
¾ подобрать поперечные сечения всех участков бруса,
¾ определить нормальные напряжения и осевые перемещения.
Решение:
Определение продольной силы
Разобьём брус на участки. Границы участков определяются сечениями, где изменяются поперечные размеры, материал, приложенные внешние нагрузки (рисунок 2.4).
Для определения продольных сил воспользуемся методом сечений (РОЗУ). Мысленно рассечём брус в пределах участка 1 и отбросим левую часть бруса. Для уравновешивания силы F1 необходимо, чтобы равнодействующая внутренних сил (продольная сила NI) равнялась этой внешней силе (рисунок 2.5):
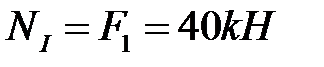 .
.
Аналогично, рассечём брус в пределах участка II и отбросим левую часть бруса. Чтобы уравновесить внешние силы F1 и F2, равнодействующая внутренних сил (продольная сила NII) должна равняться алгебраической сумме внешних сил F1,F2:
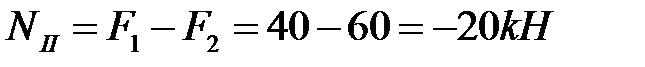 .
.
Аналогично, для остальных участков получим:
на участке III 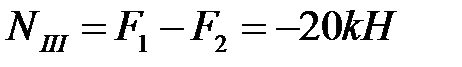
на участке IV 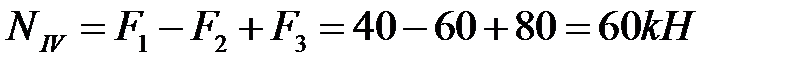 ;
;
на участке V 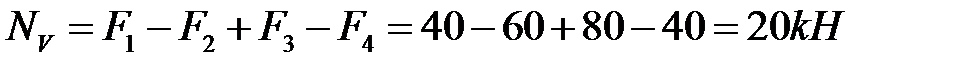 ;
;
на участке VI
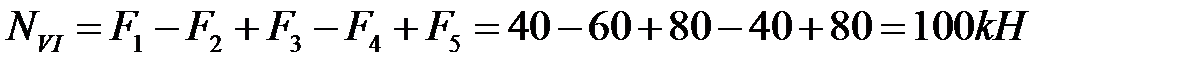 .
.
Продольные силы на IV,V и VI участках можно также определить, мысленно отбросив правую часть бруса и рассматривая равновесие его левой части. Для этого необходимо определить реакцию в заделке.
Согласно знакам продольных сил брус на участках I,IV,V,VI будет растягиваться, а на участках II, III - сжиматься.
В соответствии с полученными результатами строим эпюру продольных сил (эпюра N, рисунок 2.5).
Определение допускаемых напряжений для материала
Для решения проектной задачи по методу допускаемых напряжений необходимо их определить.
Механические характеристики материала определяются по таблице приложения С1, а коэффициенты запаса прочности материала по рекомендациям приложения С2.
Для материала Ма1 – бронза имеем:
модуль Юнга - Е1= 105МПа; предел текучести σТ=150 МПа; коэффициент запаса прочности nσ=1,5.
Для материала Ма2 – сталь имеем:
модуль Юнга – Е2= 2·105МПа; предел текучести σТ=240 МПа; коэффициент запаса прочности nσ=1,5.
Для материала Ма3 – чугун имеем:
модуль Юнга – Е3= 1,2·105МПа; предела текучести нет (т.к. материал – хрупкий), выбираем временное сопротивление при растяжении σВ=180МПа (т.к. участок имеет положительное значение продольной силы – растягивается); коэффициент запаса прочности nσ=3.
В результате, определяем [s]1=100МПа, [s]2=160МПа, [s]3=60МПа.
