Линейная интерполяция в MathCad

Функция linterp выполняет линейную интерполяцию данных между всеми соседними точками:

Интерполяция сплайнами

Кусочно-полиномиальная интерполяция выполняет приближение функции на серии последовательных отрезков. Поэтому в точках соединения отрезков функция будет иметь угловые точки (разрывы производных). Физические процессы, как правило, описываются непрерывными гладкими (с непрерывной производной) функциями.

Такая гладкая интерполяция выполняется так называемыми «сплайнами».

Например, если построить параболу 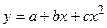, проходящую через две соседние точки, то можно определить только два коэффициента — третий коэффициент останется свободным. Точно также строится парабола по следующим двум точка, и снова один коэффициент свободный. Все свободные коэффициенты вычисляются так, чтобы производные функции в граничных точках всех смежных отрезков были бы равны.

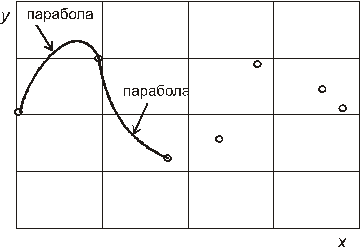
Такая интерполяция называется сплайнами.

Она более физична, чем кусочно-полиномиальная.

Ниже приведен пример использования указанных функций.

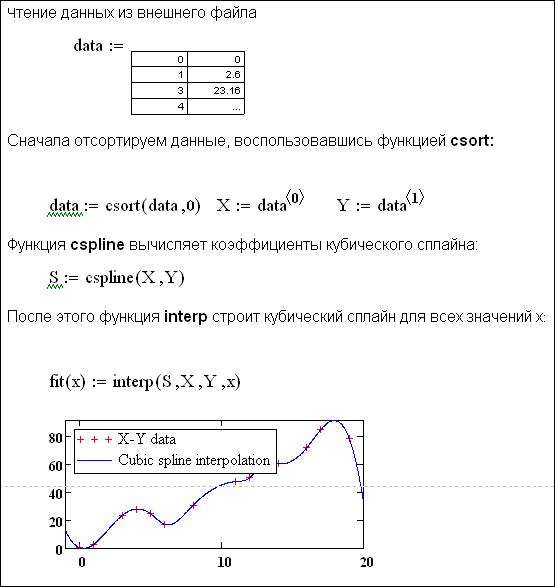
Регрессионный анализ

Регрессионный анализ имеет цель восстановления физической зависимости по экспериментальным данным.

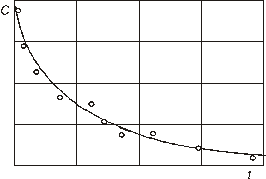
В этой задаче можно подбирать физическую зависимость формально, например, в виде какого-нибудь многочлена. Так иногда и поступают, если физика процесса неизвестна.

Однако, принципиально важно все же опирать на физику процесса, то исследователь должен указать вид функции, которая должна восстанавливаться по экспериментальным данным. Если приведенные на графике данные описывать прямой линией или синусоидой, то такая аппроксимация будет заведомо плохой. Если же мы знаем, что данные соответствуют реакции первого порядка, то есть будем подбирать функцию вида

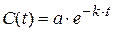
то в данном случае приближение будет вполне разумным. Формально задача сведется к отысканию коэффициентов a и k в последнем соотношении.

Определение вида функции целиком возложена на исследователя, и никакие формальные методы в этом помочь не могут.

Итак, задача состоит в том, чтобы подобрать функцию (соответствующую физике задач) в каком-то смысле близкую к исходным экспериментальным данным, в предположении, что имеются случайные ошибки эксперимента, которые и обуславливают отклонения экспериментальных точек от физической кривой.

Требуется уточнить, в каком смысле мы понимаем близость физической функции к экспериментальным данным. Наиболее распространенным методом для этого является так называемый метод наименьших квадратов.

Согласно этому методу функция близка к исходным данным, если

сумма квадратов отклонений экспериментальных данных от физической зависимости минимальна.

Проиллюстрируем это на простейшем примере, когда физическая зависимость является линейной (эта задача называется линейной регрессией).

Суть вычислений не меняется и для более сложных функций.