Геометрична інтерпретація сум Дарбу

Будемо вважати, що функція f(x) – неперервна і невід’ємна на [a,b].

Побудуємо графік функції

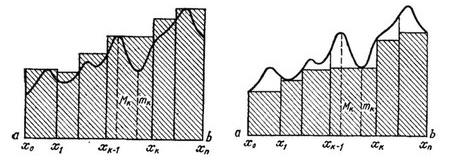
s – з геометричної точки зору уявляє собою площу ступінчатої фігури, що цілком міститься в криволінійній трапеції.

S – з геометричної точки зору уявляє собою площу ступінчатої фігури, що містить криволінійну трапецію.

Властивості сум Дарбу

Властивість 1.Нехай s₁, S₁ – нижня і верхня суми Дарбу, що відповідають розбиттю Т₁[a,b], а s₂, S₂ – суми Дарбу, що відповідають розбиттю Т₂[a,b]. Причому всі точки ділення Т₁ міститься серед точок ділення Т₂, тоді виконується нерівність: 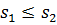, 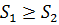. Тобто при додаванні точок ділення нижня сума Дарбу не зменшується, а верхня не збільшується.

Достатньо довести цю властивість для випадку, коли додається одна точка.

Нехай ця точка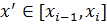

Тоді введемо позначення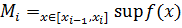

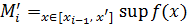
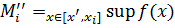
Доведемо, що 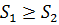, для цього знайдемо різницю S₂-S₁

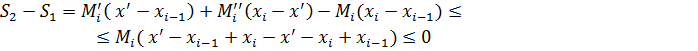
Отже, .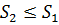

Властивість 2.Нехай s₁, S₁ – суми Дарбу, що відповідають розбиттю Т₁, а s₂, S₂ – суми Дарбу, що відповідають розбиттю Т₂.

Тоді нижня сума Дарбу одного розбиття не перевищує верхню суму іншого.

,

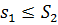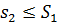
Введемо розбиття Т₃, що складається з точок ділення розбиття Т₁ і Т₂.

s₃, S₃ – суми Дарбу розбиття Т₃

Тоді з властивості 1 для розбиття Т₁ і Т₃ випливає 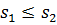, 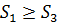(1)

З властивості 1 для Т₂ і Т₃ випливає 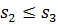, 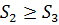(2)

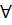розбиття (і для Т₃) одержимо, що 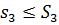(3)

З (1), (2), (3) випливає, що 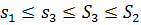, тобто .

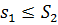Аналогічно для .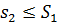

ІНТЕГРАЛИ ДАРБУ

Зауваження! Множина нижніх сум Дарбу, що відповідають різним розбиттям сегменту 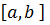обмежена зверху будь-якою верхньою сумою. Аналогічним чином верхніх сум Дарбу, що відповідають різним розбиттям сегменту [a,b] обмежена знизу будь-якою нижньою сумою.

Означення 1. Нижнім інтегралом Дарбу 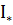називається точна верхня межа нижніх сум Дарбу. .

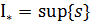Означення 2. Верхнім інтегралом Дарбу 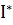називається точна нижня межа верхніх сум Дарбу.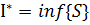

Твердження 4.Нижній інтеграл не перевищує верхнього інтегралу .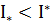

Доведення:припустимо протилежне, 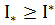=> 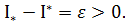З означення1 (верхньої точної межі): 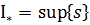: 1)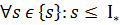
2) 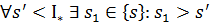. . 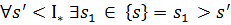Візьмемо 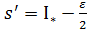, тоді 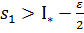(1). Аналогічно з означення 2 (нижньої точної межі): 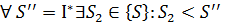=> 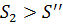, тоді 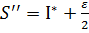=> 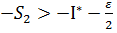(2) З (1) та (2) => 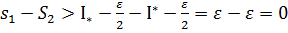=> 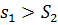, прийшли до протиріччя.

Наслідок. З означень інтегралів Дарбу => виконується 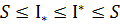для будь-якого розбиття

Теорема(про існування визначеного інтегралу)

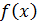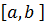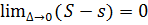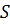Для того, щоб існував визначений інтеграл функції на необхідно і достатньо, щоб виконувались рівність , де і 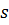- верхня та нижня суми Дарбу, - діаметр розбиття проміжку .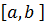

Доведення.

Необхідність: 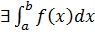=> 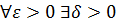: 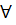розбиття 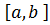, 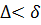. 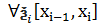: 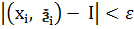, за означенням визначеного інтегралу. З останньої нерівності випливає, що 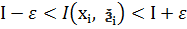(1). Для данного розбиття має місце рівність: 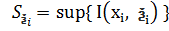; ; 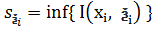Оскільки 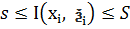=> з (1) отримаємо 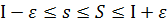. З нерівностей (1) та (2) випливає, що 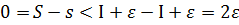, це означає,що що різницю 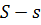можна зробити як завгодно малою => 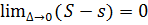, необхідність доведена.

Достатність: 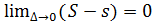. Для розбиття проміжних точок, згідно з наслідком до твердження 4: 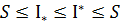=> 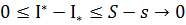(при 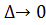). 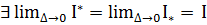=> 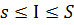(3). Нехай 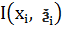- 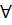з інтегрованих сум, що відповідає тому ж розбиттю сегменту, що і суми Дарбу 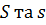. Тоді згідно із твердженням (3): 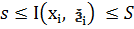(4). З нерівностей (3) та (4) => 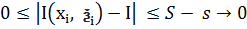(при ) =>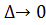

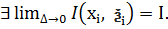
Наслідок.Оскільки виконуються рівності: 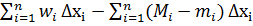= 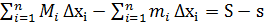, , 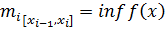, 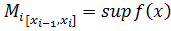то необхідну і достатню умову інтегрованості можна подати у вигляді: 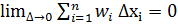(**). Величину 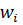називають коливанням функції 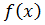на проміжку .

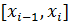КЛАС ІНТЕГРОВАНИХ ФУНКЦІЙ

1) Класс неперервних функцій

Теорема 1. Якщо функція 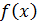неперервна на заданому проміжку 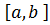, то вона інтегрована на цьому проміжку.

Доведення.Нехай функція 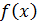непереревна на заданому проміжку 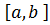, за теоремою Кантора, тоді вони рівномірна- непереревна на цьому проміжку. З наслідку до теореми Кантора випливає 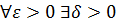: для будь-якого розбиття 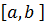, 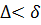: 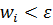. Тоді розглянемо суму 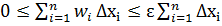= =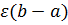> => 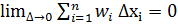функція 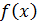інтегрована на проміжку 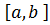, згідно з необхідною і достатньою умовою інтегрованості.

2) Класс обмежених розривних функцій

Означення. Будемо говорити, що точка х покрита інтервалом 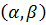, якщо вона належить цьому інтервалу.

Теорема 2. Нехай виконується умови: 1) функція 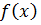обмежена на проміжку 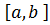, 2) 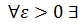скінченне число інтервалів, що покривають всі точки розривів 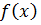і мають сумарну довжину менше ніж 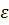, тоді функція 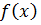інтегрована на проміжку .

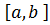Доведення.Нехай задано 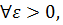тоді згідно з другою умовою теореми 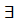скінченне число інтервалів 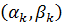(k=1,2,..,m), що покривають всі точки розриву функції 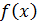на проміжку 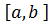і мають сумарну довжину 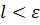. 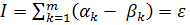(1). Всі точки проміжку 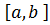, що не належать 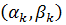утворюють скінченне число сегментів, на яких функція 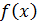неперервна і згідно з теоремою Кантора рівномірно-неперервна. Розібємо ці сегменти на часткові сегменти таким чином, щоб коливання функції 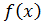на кожному з них було менше ніж 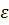і 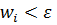(2). Таким чином, інтервал 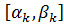, а також точки ділення сегментів на яких функція неперервна, утворюють розбиття сегмента 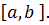Для цього розбиття утворюються наступна рівність: 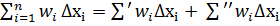(3), де сума 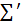побудована для точок 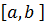, що відповідають інтервалам 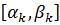, а 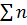- з усіх інших точок. Введемо позначення: 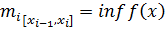, , 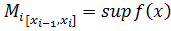, 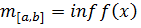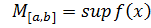. 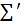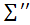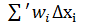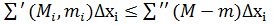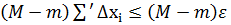Зробимо оцінку сум та : = = (4). 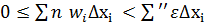= 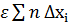(5). З нерівностей (3), (4) та (5) => 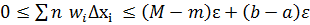= 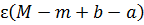. Цю суму можна зробити як завгодно малою .

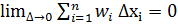Наслідок. Нехай виконуються умови: 1) функція 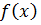обмежена на проміжку 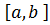, 2) функція 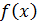має розрив в скінченному числі точок сегмента 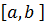, тоді функція 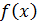інтегрована на проміжку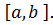

Зауваження! Нехай виконані умови: 1) функція 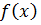неперервна на проміжку 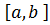, 2) функція 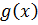обмежена на проміжку 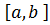та співпадає з 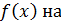проміжку 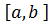за виключенням скінченного числа точок, тоді функція 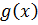також інтегрована на проміжку 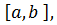при чому виконується рівність: .

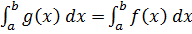3) Класс обмежених монотонних функцій

Теорема 3.Нехай функція 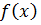обмежена та монотонна на проміжку 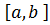, тоді вона інтегрована на цьому проміжку.

Доведення.Нехай 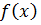не спадає і обмеженна на проміжку 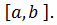Нехай задано 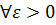. Обчислимо 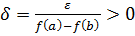. Розібємо сегмент 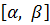точками 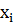таким чином, щоб діаметр покриття 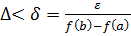. Тоді розглянемо суму 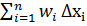= = 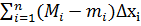= = 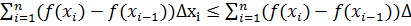= 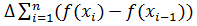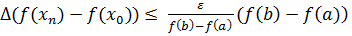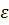, тобто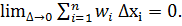

ВЛАСТИВОСТІ ВИЗНАЧЕНОГО ІНТЕГРАЛА

Коли вводилось поняття визначеного інтеграла, ми вважали, що а < b
За означенням будемо вважати:

1. Якщо a > b, то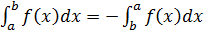

2. Якщо a = b, то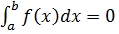

Властивість 1

Якщо функція f(x) інтегрована на [a, b], то вона інтегрована і на [b, a], при чому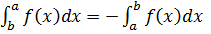

Властивість 2

Якщо функція f(x), g(x) інтегровані на [a, b], то функції [f(x) ± g(x)] також інтегровані на цьому проміжку. Причому (*)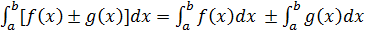

Доведення

Нечай умови теореми виконані, тобто функції f(x) та g(x) – інтегровані на [a, b]. Для будь-якого розбиття сегменту точками х; і для будь-якого вибору проміжків точок ξ_і є [x_i-1, x_i] виконується рівність рівняння інтегральних сум:

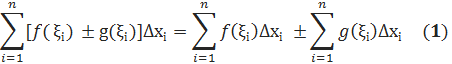
Оскільки функції f(x) і g(x) – інтегровані то існують скінчені границі ∃ 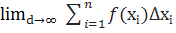, ∃ 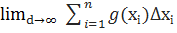(де d – діаметр розбиття). Це означає, що існує і границі лівої суми 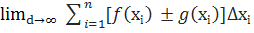, це означає що функція 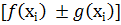інтегрована на [a, b]

Рівність (*)можна отримати з (1), якщо перейти до границі коли d прямує до 0.

Властивість 3

Якщо функція f(x) інтегрована на [a, b], то функція с·f(x) також інтегрована на [a, b]. Причому виконується рівність: 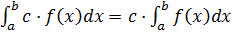Доведення аналогічно другій властивості.

Наслідок

Якщо функції f_i(x) (і = 1, 2, …, n) – інтегровані на проміжку [a, b], то їх лінійна комбінація 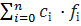( 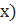також інтегрована на [a, b]. Причому виконується рівність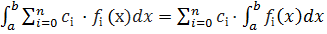

Властивість 4

Нехай f(x) інтегрована на найбільшому з проміжків [a, b], [a, c], [c, b], тоді вона інтегрована на двох інших проміжках. При чому ∀ розташуванні точок a, b, c, виконується рівність: 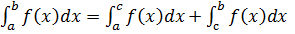(1)

Доведення

I) Якщо a < c < b. Розіб’ємо проміжок [a, b] точками x_i на n проміжків [x_i-1, x_i] Причому с – є однією з точко ділення

S – s = 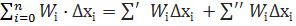(2)

W_i - коливання функції на f(x) на [x_i-1, x_i], W_i^’, W_i^’’ відповідні коливання функції на частинних проміжках [a, c], [c, b].

Оскільки функція f(x) інтегрована на [a, b], то границі 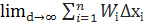= 0

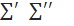- складаються з невід’ємних доданків то з (2)одержимо, що 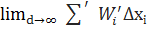= 0 , 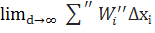= 0, а це означає, що функція f(x) інтегрована на проміжках [a, c] і [c, b] відповідно.

Запишемо очевидні рівності для інтегральних сум:

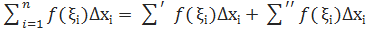(3)

Якщо в цій рівності перейти до границі, де d → 0, то перейдемо до рівності (1)

II) При будь-якому іншому розташуванні точок a, b, c, рівність (1)не змінюється. Наприклад b < a < c. Застосувавши доведення в I випадку твердження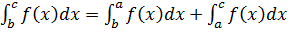

В результаті одержимо:

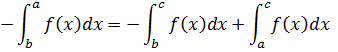
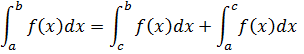
Тобто одержали рівність (1), рівність доведена.

Зауваження:

Якщо функція f(x) інтегрована на будь-яких двох проміжках з трьох проміжків [a, b], [a, c], [c, b], то вона інтегрована і на третьому також.

Властивість 5

Нехай виконуються умови:

1) функція f(x) інтегрована на проміжках [a, b];

2) ∀x є [a, b] : f(x) ≥ 0

3) a < b

Тоді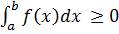

Доведення

Нехай задане ∀ розбиття сегмента [a, b] точками x_i, і вибрані ∀ 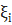є [x_i-1, x_i], тоді з II умови впевнимося, що інтегральна сума

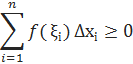
Оскільки функція f(x) інтегрована на [a, b], то існує скінчена границя:

∃

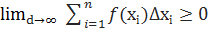
Властивість 6

Нехай виконується умови:

1) функції f(x) і g(x) – інтегровані на проміжку [a, b];

2) ∀x є [a, b] : f(x) ≤ g(x);

3) a < b;

Тоді

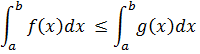
Доведення

Введемо функцію h(x) = g(x) – f(x), ця функція очевидно, що більше 0 : h(x)≥0. Ця функція задовольняє властивості 5, а це означає що виконується нерівність:

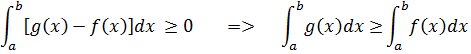
Властивість 7

Нехай виконується умови:

1) функція f(x) – інтегрована на [a, b];

2) ∀x є [a, b] : m ≤ f(x) ≤ M;

3) a < b;

Тоді виконується наступна подвійна нерівність:

m(b – a) ≤ 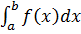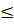M(b – a)

Доведення цієї властивості випливає з властивості 6, якщо взяти функції y=m, y = f(x) і y = f(x), y = M.

Властивість 8

Нехай виконується умова:

1) функція f(x) – інтегрована на [a, b];

2) a < b

Тоді функція |f(x)| також інтегрована на [a, b] причому виконується нерівність: | 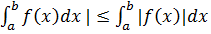(1)

Доведення

Нехай умови теореми виконані розіб’ємо проміжок [a, b] точками x_i на n частинних проміжків [x_i-1, x_i]. Застосуємо нерівність трикутника для подальшого доведення.

||α| - |β|| ≤ | α – β|(∀α, βє R) (2)

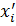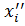∀ , : ||f( 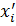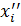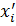)| - |f( 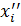)|| 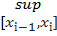≤ |f( )| – f( 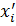)| => ||f( 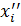)| 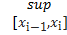- |f( )|| ≤ |f( 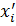)| – f( )|

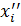Тобто 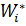≤ 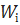(3) , де 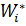, 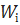– коливання f(x), |f(x)| на 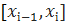. А тоді з нерівності (3)випливає наступна нерівність для сум:

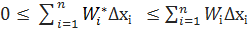(4)

Оскільки функція f(x) інтегрована на [a, b], то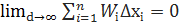

Тоді з нерівності (4)=> 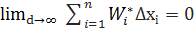це означає, що функція |f(x)| - інтегрована на [a, b]. Нерівність (1)випливає з нерівності інтегральних сум. Оскільки |f(x)| ≤ f(x) ≤ |f(x)| згідно нерівність (6), (7)|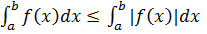

ФОРМУЛИ СЕРЕДНЬОГО ЗНАЧЕННЯ

Властивість 9.

Нехай виконані умови:

1. Функція 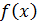– інтегрована на проміжку ;

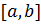2. .

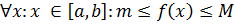Тоді має місце формула середнього значення:

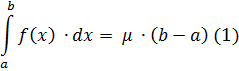
Доведення:

1) Розглянемо випадок 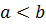, тоді за властивістю 7:

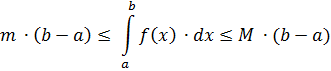
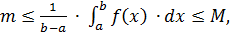
Оскільки 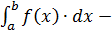існує, то .

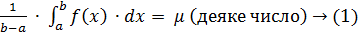2) Розглянемо тоді для проміжку 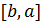виконується властивість 7. Тоді можемо записати:

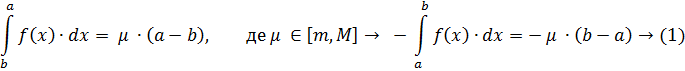
Наслідок

Якщо умови властивості 9 виконані і крім того функція 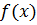– неперервна на 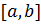, то має місце формула середнього значення для неперервної функції:

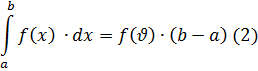
Де .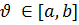

Доведення:

Нехай умови виконані, тоді за 2 теоремою Вейерштрасса функція 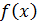досягає своїх точних верхньої і нижньої меж на 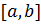. А тоді згідно з 2 теоремою Больцано-Коші для одержаного у властивості 9 числа 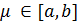знайдеться число 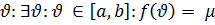, а це означає, що виконується рівність (2).