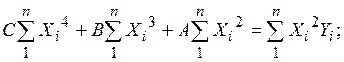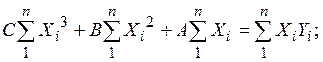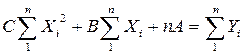Указания по выполнению

1. Серии экспериментальных данных студент выбирает из таблице 4 по предпоследней и последней цифрам шифра. Например, шифру 96836 соответствуют серии, включающие все результаты измерений X (числитель) и У (знаменатель), которые представлены в строке 3 и столбце 6.

2. Считать, что результаты измерений не содержат ошибок.

2.5.3 Порядок расчета

Обработку экспериментальных данных при изучении зависимостей целесообразно осуществлять по алгоритмам [4, с. 99-109].

1. В осях координат X и Y построить n экспериментальных то­чек с координатами X_i ,Y_i, i Î (1…20) и по характеру расположе­ния точек принять гипотезу о виде уравнения регрессии Y на X.

Таблица 4 – Исходные данные

Предпоследняя цифра шифра	Последняя цифра шифра

В качестве уравнения регрессии целесообразно использовать полином степени m:

Y = А + В∙Х + С∙Х² + ... + К∙Х^m.

В первом приближении для решения данной задачи рекомендуется принять m = 1, т.е.

Y = А + В∙Х.

2 Определить параметры уравнения регрессии по методу наи­меньших квадратов. Для этого необходимо:

– составить систему уравнений по числу рассчитываемых параметров:

; ; ; … ; ,

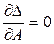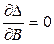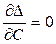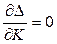где .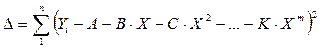

Например, для линейного уравнения регрессии система уравнений имеет вид:

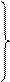
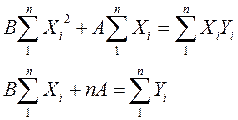
– решить систему уравнений и определить неизвестные параметры, например, для линейного уравнения регрессии решение имеет вид:

.

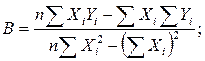
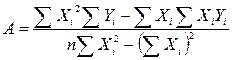3. Проверить правильность выбора вида уравнения регрессии. Для этого следует применить непараметрические критерии серий и инверсий:

– рассчитать отклонения экспериментальных значений Y_i от соответс­твующих значений Y_pi, рассчитанных для того же аргумента X_i по по­лученному уравнению регрессии:

DY_i = Y_i – Y_pi ;

– построить в осях координат X, DY полученные значения DY_i для со­ответствующих X_i;

– записать последовательность значений DY_j по мере возрастания X_j, X_j Î [l,n];

– рассчитать число серий N в полученной последовательности DY_j (под серией в данном случае понимают последовательность отклоне­ний одного знака, перед и после которой следуют отклонения про­тивоположного знака или нет вообще никаких отклонений);

– задавшись доверительной вероятностью Р ( уровнем значимости a = 1 – Р) для n = 20 определить по соответствующей таблице (таблица А.6 [4] или таблица Ж.1) допустимые границы N_1-0,5a и N_0,5a;

– рассчитать число инверсий А в полученной последовательности DY_j (под инверсией понимается событие, заключающееся в том, что DY_j > DY_jk при k > j):

,

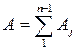где A_j – это число инверсий j - гo члена последовательности, т.е. число членов последовательности, которые, будучи расположенными в последовательности после j - ого члена, имеют значение меньшее, чем DY_j;

– задавшись доверительной вероятностью Р ( уровнем значимости a = 1 – Р) для n = 20 определить по соответствующей таблице (таблица А.7 [4] или таблица И.1) допустимые границы A_1-0,5a и A_0,5a;

– сравнить А с A_1-0,5a и A_0,5a;

Если выполняются неравенства

N_1-0,5a < N £ N_0,5a;

A_1-0,5a < A £ A_0,5a,

то с выбранной доверительной вероятностью Р можно считать, что отклонения экспериментальных значений Y_i, от соответствующих зна­чений Y_рi найденного уравнения регрессии являются случайными, не содержат аддитивного, мультипликативного или колебательного трендов, т.е. рассчитанное уравнение регрессии достоверно описывает экспериментально исследуемую зависимость между величинами X и Y.

Если хотя бы одно из указанных выше неравенств, не выполня­ется, то следует пересмотреть выбор вида уравнения регрессии. В частности, можно увеличить степень полинома m на единицу и повто­рить вычисления по описанному выше алгоритму. Например, для полинома второй степе­ни:

Y = А + В∙Х + С∙Х².

Сцелью определения параметров уравнения регрессиив данном слу­чае необходимо решить систему уравнений: