Формула Тейлора
Замена функции ее дифференциалом дает возможность получить приближенные формулы. Эти формулы можно уточнить, используя дифференциалы высших порядков.
Рассмотрим многочлен
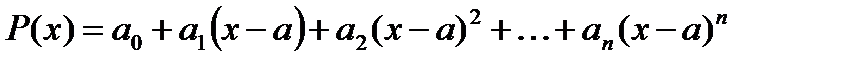 . (1)
. (1)
Его можно разложить по степеням. Коэффициенты можно найти, положив 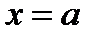 ,
, 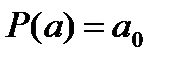 . Продифференцируем
. Продифференцируем
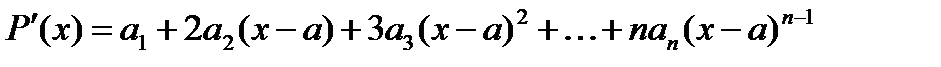 ,
, 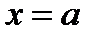 ,
, 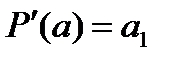 .
.
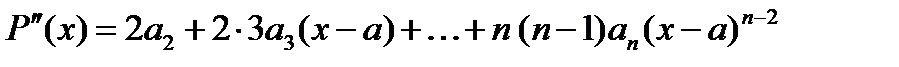 ,
, 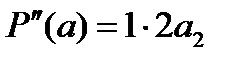 ,
,
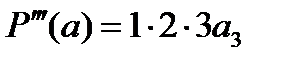 ,
,
…,
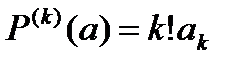 .
.
Следовательно, 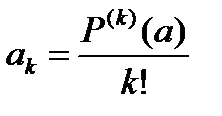 . Тогда
. Тогда
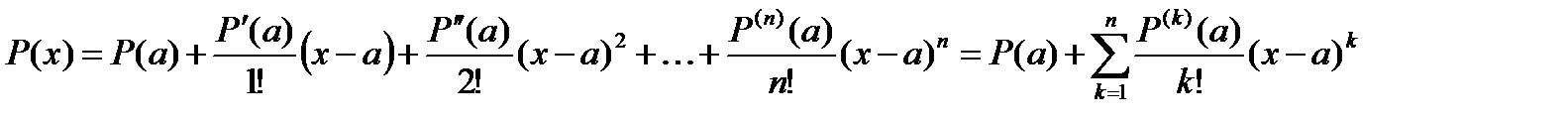 . (2)
. (2)
Если вместо 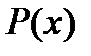 взять
взять 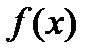 произвольно, то (2) уже не будет справедлива, но если обозначить отличие через
произвольно, то (2) уже не будет справедлива, но если обозначить отличие через 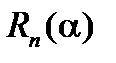 (остаточный член), то можно написать
(остаточный член), то можно написать
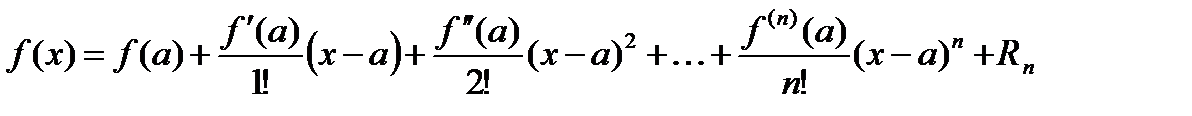 . (3)
. (3)
Это и есть формула Тейлора. При 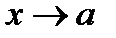
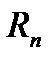 имеет по крайней мере
имеет по крайней мере 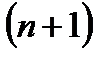 -й порядок малости по сравнению с
-й порядок малости по сравнению с 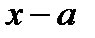 , то есть более высокий порядок, чем последний из выписанных «точных» членов в формуле (3).
, то есть более высокий порядок, чем последний из выписанных «точных» членов в формуле (3).
Формула (3) дает возможность заменить функцию 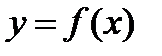 многочленом
многочленом 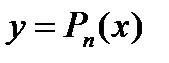 с соответствующей степенью точности, равной значению
с соответствующей степенью точности, равной значению 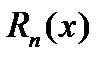 .
.
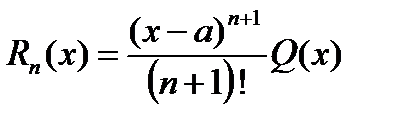 .
.
Форма Лагранжа для остаточного члена
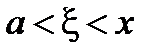
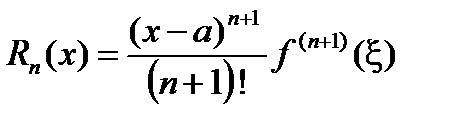 , (4)
, (4)
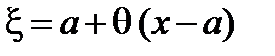 ,
, 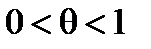 .
.
Если 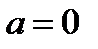 , то
, то
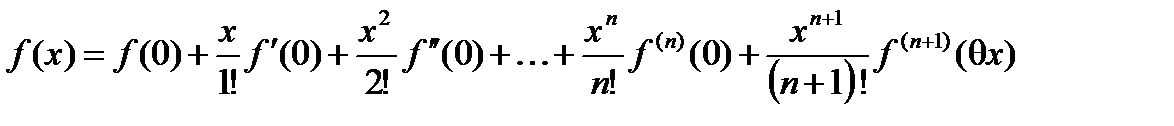 – (5)
– (5)
формула Маклорена.
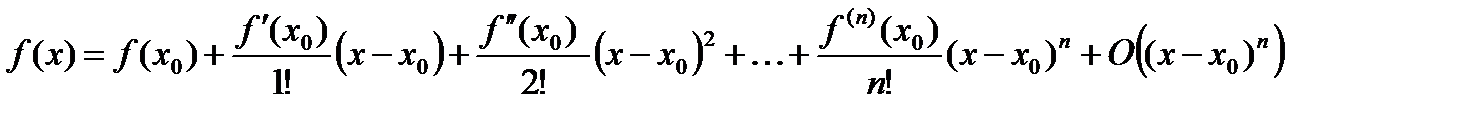 . (6)
. (6)
Формула (6) называется формулой Тейлора с дополнительным членом в форме Пеано.
