Задача о распространении тепла в цилиндрической стенке также одномерная, если ее рассматривать в цилиндрических координатах. температура изменяется только вдоль радиуса r, а по длине и по ее периметру остается неизменной.
В соответствии с законом Фурье, тепловой поток через однородную цилиндрическую стенку длиной l определяется по формуле: 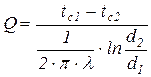 ,
,









Тепловой поток Q через цилиндрическую стенку можно отнести к единице длины l:
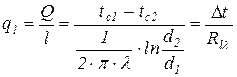 ,
,
| Рисунок 9.5 - Изменение температуры по толщине однородной цилиндрической стенки | |
где q
l - линейная плотность теплового потока, Вт/м;
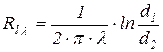 - линейное термическое сопротивление теплопроводности трубы.
- линейное термическое сопротивление теплопроводности трубы.
При значениях d2/d1 близких к единице расчеты Rl 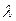 должны производиться с высокой точностью, т.к. при округлении d2/d до одного знака после запятой погрешность вычисления логарифма будет больше 10%. С точностью до 4% при d2/d1 < 2 в практических расчетах рекомендуется пользоваться формулой для плоской стенки:
должны производиться с высокой точностью, т.к. при округлении d2/d до одного знака после запятой погрешность вычисления логарифма будет больше 10%. С точностью до 4% при d2/d1 < 2 в практических расчетах рекомендуется пользоваться формулой для плоской стенки:
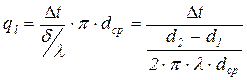 ,
,
где dcp=0,5(d1+d2) - средний диаметр трубы.
В толще однородной цилиндрической стенки температура изменяется по логарифмическому закону.
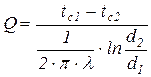 ,
,









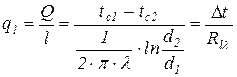 ,
,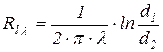 - линейное термическое сопротивление теплопроводности трубы.
- линейное термическое сопротивление теплопроводности трубы.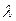 должны производиться с высокой точностью, т.к. при округлении d2/d до одного знака после запятой погрешность вычисления логарифма будет больше 10%. С точностью до 4% при d2/d1 < 2 в практических расчетах рекомендуется пользоваться формулой для плоской стенки:
должны производиться с высокой точностью, т.к. при округлении d2/d до одного знака после запятой погрешность вычисления логарифма будет больше 10%. С точностью до 4% при d2/d1 < 2 в практических расчетах рекомендуется пользоваться формулой для плоской стенки: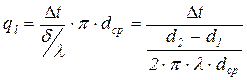 ,
,