Формула Тейлора с остаточным членом в форме Лагранжа и Коши

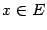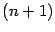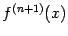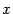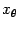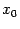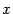Теорема 6.2 (остаток в формуле Тейлора в форме Лагранжа) Пусть при всех существует -я производная . Тогда для любого существует точка , лежащая между и (то есть 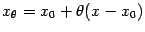при 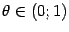), такая что

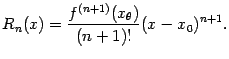
(Остаточный член формулы Тейлора, представленный в таком виде, называется остаточным членом в форме Лагранжа.)

Доказательство. Это доказательство не столь прямолинейное, как в предыдущей теореме. Рассмотрим вспомогательную функцию 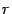переменного 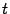, изменяющегося в рассматриваемой окрестност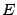и точки 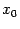. Эта функция будет зависеть также от параметра :

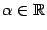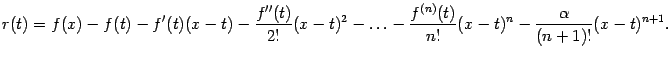
Подберём такое значение параметра 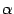, равное 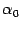, чтобы при 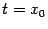функция обращалась в 0: 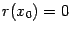. Фиксируем такое значение .

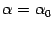Тогда функция 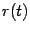удовлетворяет условиям теоремы Ролля на отрезке 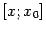(или 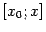, если 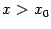): 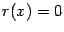, что очевидно по определению функции 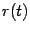; 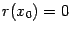согласно выбору параметра; дифференцируемость на 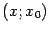и непрерывность в точках 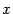и 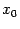следуют из предположенных свойств функции 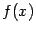. По теореме Ролля существует такая точка 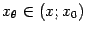, что

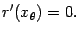
Однако нетрудно подсчитать, находя производные произведений в определении функции 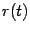, что

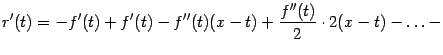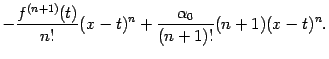Все слагаемые в начале правой части, включая обозначенные многоточием, взаимно уничтожаются, так что получаем

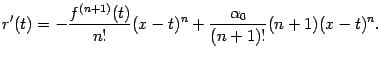
Подстановка 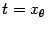даёт

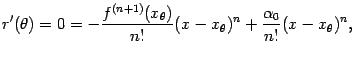
откуда следует, что

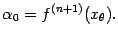
Теперь вспомним, что значение параметра мы выбрали так, что 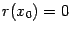. Подставив найденное значение 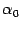в выражение для , получим:

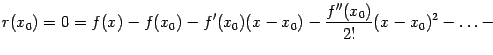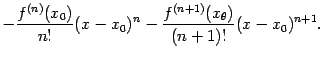Отсюда получаем, наконец,

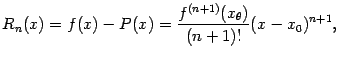
Что и требовалось доказать.

Общие свойства предела!

Определение 2.5. Последовательность называется постоянной, если

Уп:х_п=а = соп$1.

Определение 2.6. Последовательность называется финально постоян­ной, р^пи она постоянна, наминая с некоторого номера:

N х_п=а = соп81.

Замечание 2.2. Конечное число членов последовательности не влияет на её сходимость.

Теорема 2.1.

Финально постоянная последовательность сходится;

если 1ипх_п = А то VУ(А) содержит все члены последователь-

Л-*»

ности за исключением конечного числа;если последовательность имеет предел, то он единственный:

Иша:_п = а, а Итх„ = а₂ => а, = а₂;

п—юо Л—>оо

сходящаяся последовательность ограничена:

1ЮШ = а=> ЭМ : \/п Ы < М.

П—¹ '

4 Докажем 3: пусть о, * а₂,а₂ = а, + Д,Д > 0 =>

Ншх_п=а_]: \/е=— 3N^:Уп>N^ \х_п-а_]\<е,

Нш х„ = а₇: Уе = — 3//,: Уп > 1Ё I х„ - а, |< е.

„_*» " 2

Если N := тах-^рЛ^}, то л:_я е У(о,)пУ(я₂), но ^(а₁)пУ(й₂) = 0=> приходим к противоречию, т.е. а^=а₂ => пре­дел единственный. ►

■4 Докажем 4: Нтл = а => Пусть € = 1 =>

Л-)оо

ЭЛГ = N(6) :\/п>и\х_П-а\<1=>

.к,, е (а-1,а + 1) |лг„ |< А:=тах(|я + 1|,|а-1|). Возьмем М := тах(А,| л:, |,| х₂х_м |), тогда |д:„| <МУп. ►

Предел сложной функции:

Из существования пределов f ( x ) в точке a и g ( y ) в точке f ( a ) следует существование предела сложной функции g ( f ( x )) в точке a .