Индивидуальные задачи к заданию 5
| №№ | f(x) | №№ | f(x) |
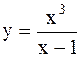 | 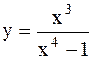 | ||
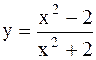 | 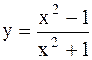 | ||
 |  | ||
 |  | ||
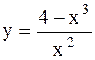 | 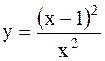 | ||
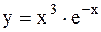 | 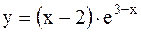 | ||
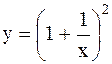 | 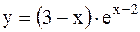 | ||
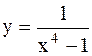 | 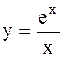 | ||
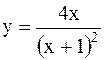 | 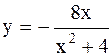 | ||
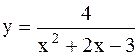 | 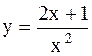 | ||
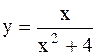 | 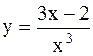 | ||
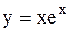 | 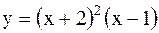 | ||
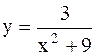 | 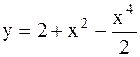 | ||
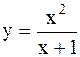 | 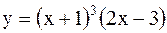 |
Продолжение табл.1.4
| №№ | f(x) | №№ | f(x) |
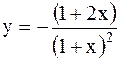 | 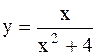 | ||
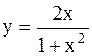 | 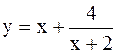 | ||
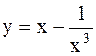 | 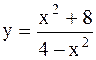 | ||
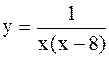 | 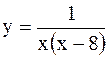 | ||
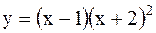 | 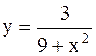 | ||
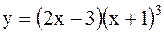 | 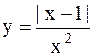 | ||
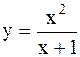 | 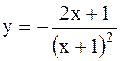 | ||
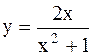 | 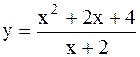 | ||
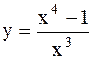 | 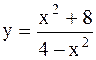 | ||
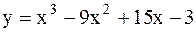 | 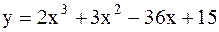 | ||
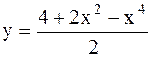 | 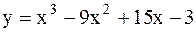 |
Контрольные вопросы
1. Сформулируйте определение предела функции.
2. Какая величина называется бесконечно малой?
3. Сформулируйте теоремы о пределах.
4. Запишите формулу первого замечательного предела. Перечислите следствия.
5. Запишите формулу второго замечательного предела. Перечислите следствия.
6. Дайте определение производной функции.
7. Приведите уравнение касательной и нормали к кривой в данной точке.
8. Какова связь между дифференцируемостью и непрерывностью функции в точке.
9. Дайте определение дифференциала функции. Приведите связь между дифференциалом и производной функции.
10. Сформулируйте лемму Ферма.
11. Сформулируйте теорему Лагранжа о среднем.
12. Сформулируйте теорему Коши о среднем.
13. Сформулируйте правило Лопиталя.
14. Запишите формулу Тейлора.
Список рекомендуемой литературы
1. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.I. – М.:Наука, 1985.
2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. Т.I. – М.:Наука, 1988.
