Аналитический способ синтеза регулятора

ПОЛОЖЕНИЯ

Аналитический способ синтеза предполагает определение полной модели РП, полученной в соответствии с выражением

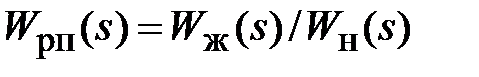(6.1)

с применением программы в Command Window [18]. Применение данного подхода позволяет обойтись без построения ЛАЧХ РП и не требует дополнительных графических построений и расчетов, что, в свою очередь, упрощает решение задачи синтеза в целом.

Полученная модель наиболее адекватно соответствует заданным точностным характеристикам и обеспечивает достаточную плавность переходных процессов. На основании решения (6.1) производится дискретная аппроксимация аналоговой модели РП с применением формулы трапеций. Таким образом, задача сводится к следующим этапам:

- расчет параметров желаемой передаточной функции 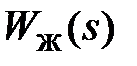на основании ошибки по скорости Da_W, ошибки по ускорению Da_e, максимальной угловой скорости нагрузки 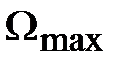, максимального углового ускорения нагрузки 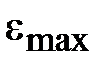и показателя колебатеьности М;

- расчет передаточной функции неизменяемой части системы по формуле ;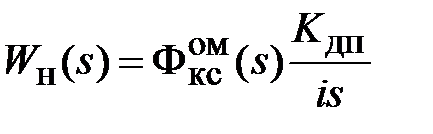

- составление программы решения задачи в соответствии с формулой (6.1);

- определение дискретной передаточной функции РП 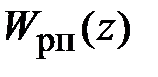с применением формулы трапеций;

- определение коэффициентов матриц A, B, C, D векторно-матричной модели цифрового регулятора положения.

ПРИМЕР ПРОГРАММНОЙ РЕАЛИЗАЦИИ РЕГУЛЯТОРА

ПОЛОЖЕНИЯ ДЛЯ ЭЛЕКТРОПРИВОДА С АСТАТИЗМОМ

ВТОРОГО ПОРЯДКА. МОДЕЛИРОВАНИЕ КОНТУРА

ПОЛОЖЕНИЯ

Пример 6.1. Синтезировать регулятор положения на основе критерия динамической точности системы. Получить алгоритм работы цифрового регулятора положения. При решении задачи считать период квантования Т₀ = 0,001 с. Для расчётов принять следующие параметры:

- максимальная угловая скорость нагрузки 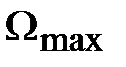= 10 град/с;

- максимальное угловое ускорение нагрузки 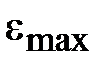= 6 град/с²;

- ошибка по скорости Da_W = 10 мин;

- ошибка по ускорению Da_e = 35 мин;

- передаточное число редуктора ;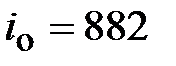

- показатель колебательности М = 1,1;

- коэффициент передачи вращающегося трансформатора

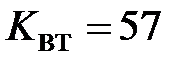В/рад.

Моментную составляющую ошибки определить при отработке квадратично возрастающего момента сопротивления .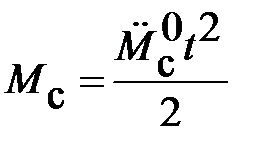

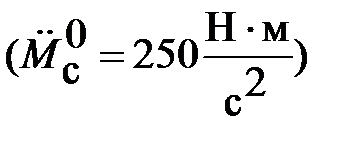Параметры контура скорости принять из примера 4.2.

Решение. Определяем параметры желаемой передаточной функции ЭП (5.6). Коэффициент передачи по ускорению будет равен

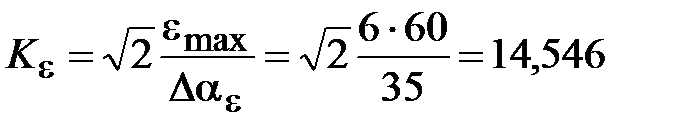с^{– 2}.

Значение базовой частоты определится по формуле (5.4) и будет равно

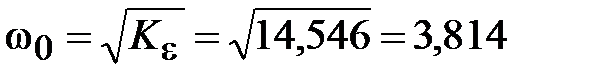с^{– 1}.

По выражениям (5.7) рассчитываем постоянные времени

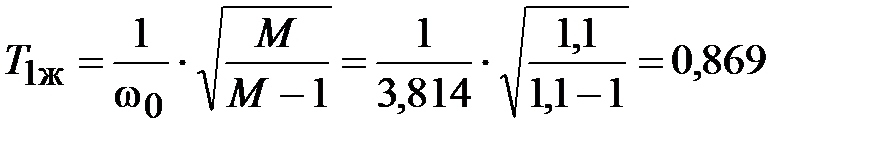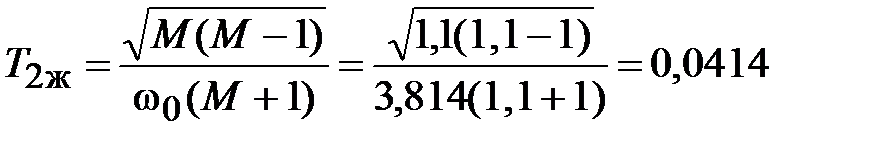с;

с.

С учётом проведённых расчётов запишем желаемую передаточную функцию ЭП с астатизмом второго порядка

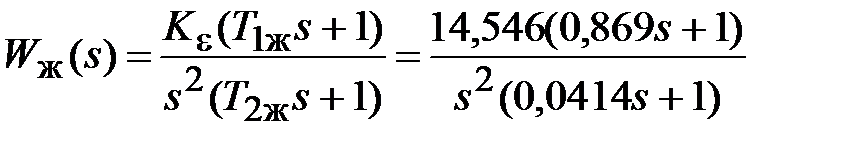. (6.2)

Передаточная функция неизменяемой части

.

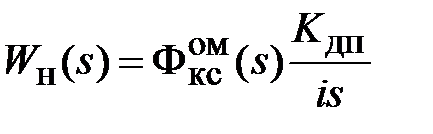Так как контур скорости настроен на оптимум по модулю, то передаточная функция замкнутого контура может быть записана в виде

.

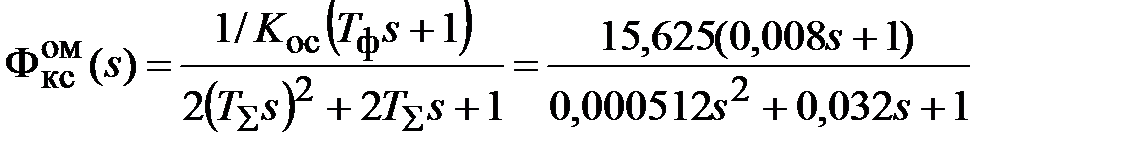Тогда

.

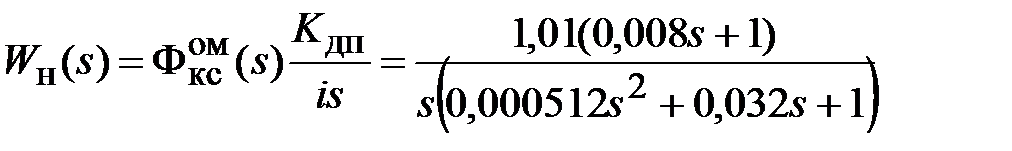Для определения передаточной функции регулятора положения составляем следующую программу:

num1=[14.546*0.869 14.546];

den1=[0.0414 1 0 0];

sys1=tf(num1, den1);

num2=[1.01*0.008 1.01];

den2=[0.000512 0.032 1 0];

sys2=tf(num2, den2);

sys3=sys1/sys2

sys3 =

0.006472 s^4 + 0.4119 s^3 + 13.11 s^2 + 14.55 s

-----------------------------------------------

0.0003345 s^4 + 0.04989 s^3 + 1.01 s^2

Полученную передаточную функцию регулятора положения можно упростить:

num=[0.006472 0.4119 13.11 14.55 0];

den=[0.0003345 0.04989 1.01 0 0];

sys=tf(num, den);

minreal(sys)

ans =

19.35 s^3 + 1231 s^2 + 3.919e04 s + 4.35e04

-------------------------------------------

s^3 + 149.1 s^2 + 3019 s

Для определения передаточной функции цифрового регулятора положения 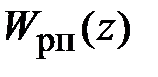с применением формулы трапеций составим программу:

num=[19.35 1231 3.919e04 4.35e04];

den=[1 149.1 3019 0];

fs=1000;

[numd, dend]=bilinear(num, den, fs)

numd =

18.576410954661924 -54.547965297744668 53.403203894058869

-17.431609097327989

dend =

1.000000000000000 -2.858534057438136 2.719875691054094

-0.861341633615959

Коэффициенты матриц векторно-матричной формы записи уравнений цифрового регулятора скорости получим с применением программы:

num=[18.576410954661924 -54.547965297744668 53.403203894058869

-17.431609097327989];

den=[1.000000000000000 -2.858534057438136 2.719875691054094

-0.861341633615959];

[A, B, C, D]=tf2ss(num, den)

A =

2.858534057438136 -2.719875691054094 0.861341633615959

1.000000000000000 0 0

0 1.000000000000000 0

B =

C =

-1.446661918876679 2.877675311442928 -1.430972938918092

D =

18.576410954661924

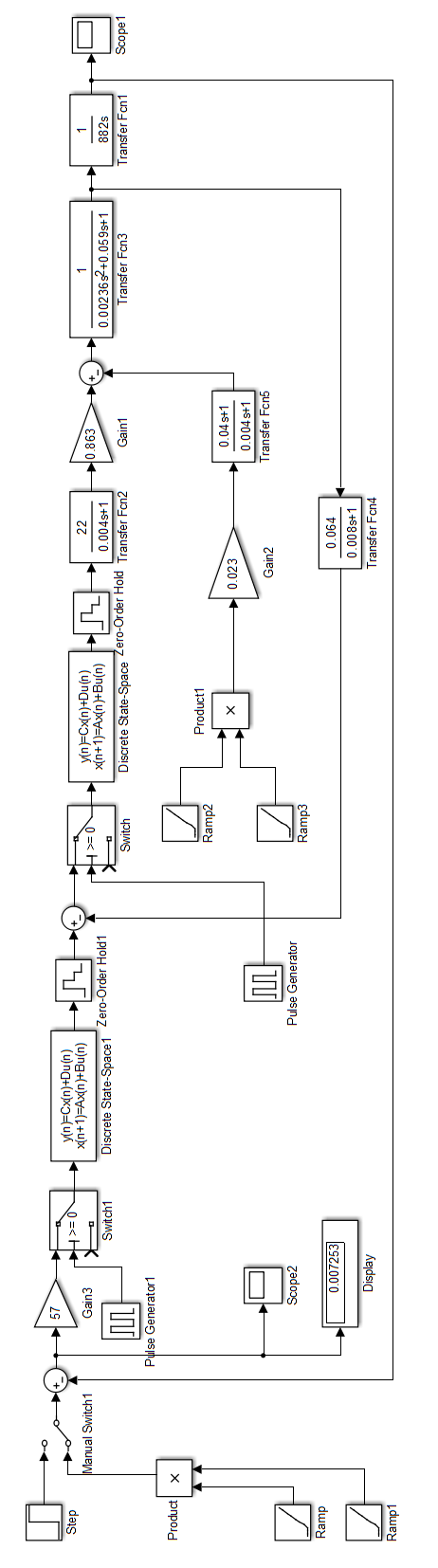
Переходим к построению и моделированию ССДМ ЭП, показанной на рис. 6.1.

Рис. 6.1. Структурная схема динамической модели электропривода в среде MatLab

Для формирования квадратично возрастающих воздействи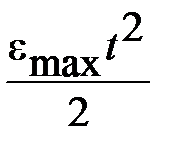й и 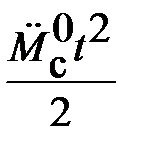используются, соотвтетственно, блоки Ramp, Ramp1 и Ramp2, Ramp3. Результаты моделирования показаны на рис. 6.2-6.4.

α(t), рад

t, c

Рис. 6.2. Переходная характеристика системы по задающему воздействию

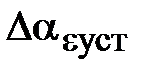, рад

t, c

Рис. 6.3. График ошибки системы при квадратично возрастающем

задающем воздействии

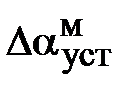, рад

t, c

Рис. 6.4. График моментной составляющей ошибки системы

при квадратично возрастающем моменте сопротивления

Анализ графика (рис. 6.2) показывает, что следящий позиционный ЭП отрабатывает ступенчатое воздействие 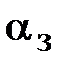примерно за 3,0 с с перерегулированием 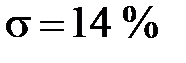и числом колебаний N < 1, что соответствует заданному показателю колебательности М = 1,1.

Поскольку контур положения содержит ПИД-регулятор положения, очевидно, что при ступенчатом и линейно возрастающем задающем воздействии статическая ошибка и ошибка по скорости будут равны нулю. На рис. 6.3 представлена характеристика при отработке типового задающего воздействия 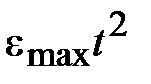/2. Установившаяся ошибка системы 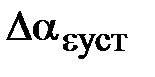составляет около 25 мин. Моментная составляющая ошибки 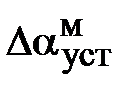при отработке квадратично возрастающего момента сопротивления 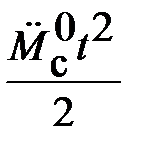составляет 0,1 мин по истечении 4 с (рис. 6.4).

Графики переходных процессов получены с применением блока MultiPlot Graph из раздела Robust Control Toolbox библиотеки Simulink.