В высшей математике всегда стремимся складывать и умножать, а не вычитать и делить

Пример 6

Решить систему линейных уравнений:

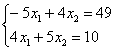
8) Правило Крамера

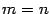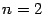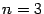Рассмотрим частный случай системы линейных уравнений (15.1), когда , то есть когда число уравнений совпадает с числом неизвестных. Именно такие системы при или рассматриваются в школе.

Если число уравнений равно числу неизвестных, то матрица 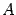исходной системы -- квадратная, порядка 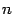, 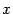и 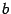-- столбцы высоты 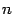. Предположим, что 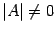. Тогда по теореме 14.1существует обратная матрица. Умножив слева обе части равенства (15.2) на 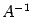, получим

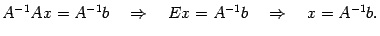
Таким образом, система уравнений (15.1) имеет единственное решение и оно в матричной форме может быть записано в виде

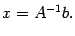(15.3)

Это так называемый матричный способ решения системы линейных уравнений.

Введем следующие обозначения. Пусть 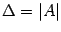, 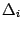-- определитель матрицы, полученной из матрицы 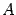заменой столбца с номером 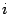на столбец 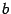свободных членов, :

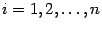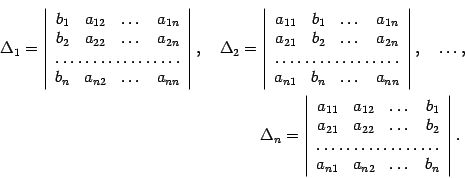
Теорема 15.1 (Правило Крамера) Если в системе 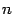линейных уравнений с 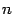неизвестными 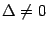, то система имеет решение и притом единственное. Это решение задается формулами

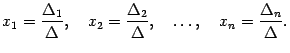
Доказательство. По теореме 14.1 обратная матрица находится по формуле

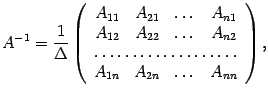
где 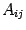-- алгебраические дополнения. Тогда из (15.3) следует, что

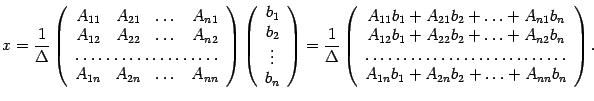
Заметим, что по формуле (14.13) разложение определителя 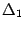по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя 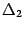по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому 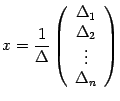, откуда и следует утверждение теоремы.

Пример 15.1 Решите систему уравнений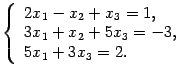

Решение. Выписываем матрицу системы 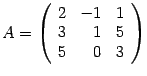и столбец свободных членов .

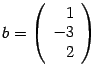Находим определитель системы: 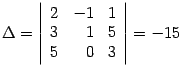. Определитель отличен от нуля, следовательно, можно применить правило Крамера. Находим дополнительные определители:

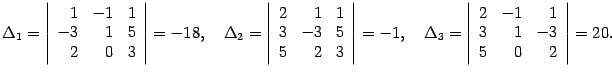
Итак,

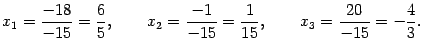
Ответ: .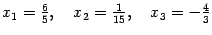

Замечание 15.1 При кажущейся простоте правила Крамера применяется оно для систем более, чем из трех уравнений, только в каких-то исключительных случаях. Дело в том, что вычисление определителей требует выполнения большого числа арифметических операций и существует способ, требующий меньшей вычислительной работы. Этот способ будет описан позже.

Замечание 15.2 При решении системы уравнений приходится выполнять довольно большой объем вычислений. Поэтому велика вероятность ошибки. Чтобы обнаружить эту ошибку, рекомендуется выполнить проверку ответа, то есть подставить полученные значения неизвестных в уравнения системы. Если все уравнения превратятся в верные равенства, то решение найдено верно. В противном случае при вычислениях где-то допущена ошибка.

9) Метод Гаусса (последовательного исключения неизвестных).
Примеры решений для чайников

Продолжаем рассматривать системы линейных уравнений. Этот урок является третьим по теме. Если Вы смутно представляете, что такое система линейных уравнений вообще, чувствуете себя чайником, то рекомендую начать с азов на странице Как решить систему линейных уравнений? Далее полезно изучить урок Правило Крамера. Матричный метод.

Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто!Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.

Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА.Необходимо уметь складывать и умножать!Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.

Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:

1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной).

Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решениялюбой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случаеприведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статьяНесовместные системы и системы с общим решением. Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.

Вернемся к простейшей системе с урока Как решить систему линейных уравнений?
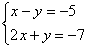и решим ее методом Гаусса.

На первом этапе нужно записать расширенную матрицу системы:
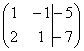. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.

Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: 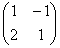. Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: 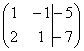. Любую из матриц можно для краткости называть просто матрицей.

После того, как расширенная матрица система записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.

Существуют следующие элементарные преобразования:

1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки: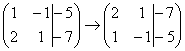

2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .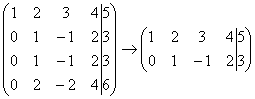

3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следуетудалить. Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули.

4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Рассмотрим, например, матрицу 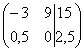. Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: 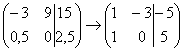. Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.

5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим нашу матрицу из практического примера: 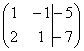. Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: 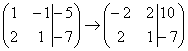, и ко второй строке прибавляем первую строку умноженную на –2: 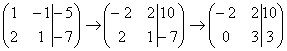. Теперь первую строку можно разделить «обратно» на –2: 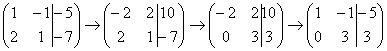. Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.

На практике так подробно, конечно, не расписывают, а пишут короче:

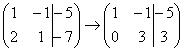
Еще раз: ко второй строке прибавили первую строку, умноженную на –2. Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:

«Переписываю матрицу и переписываю первую строку: »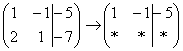

«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: 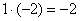, и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »

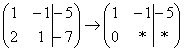«Теперь второй столбец. Вверху –1 умножаю на –2: 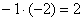. Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »

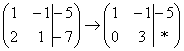«И третий столбец. Вверху –5 умножаю на –2: 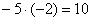. Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »

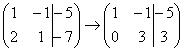Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.