Динамический синтез маховика

4.1 Определение момента инерции маховика

Неравенство работ сил движущих и сил сопротивления, а также непостоянство приведенного момента инерции механизма приводят к изменению скорости ведущего звена. При установившемся периодическом режиме движения это вызывает периодические колебания угловой скорости. Для машин, выполняющих различные технологические процессы, эти колебания допустимы лишь в определенных пределах, устанавливаемых практикой эксплуатации оборудования. Критерием допускаемой величины относительного изменения скорости принят коэффициент неравномерности хода машины

(4.1)

Предварительный расчет проектируемой машины может показать полное несоответствие неравномерности хода заданной величине .

Практически задачу регулирования периодической неравномерности хода машины решают посредством установки дополнительной, так называемой маховой массы. Такую массу обычно конструктивно оформляют в виде маховика - массивного диска или колеса со спицами. Маховые массы накапливают кинетическую энергию на участках цикла, имеющих приведенный момент движущих сил больший, чем приведенный момент от сил сопротивления, когда скорость ведущего звена возрастает. На участках с обратным соотношением этих моментов скорость снижается и маховые массы отдают накопленную кинетическую энергию, выполняя роль механического аккумулятора энергии.

Динамический синтез маховика рассмотрим на примере.

Исходные данные: структурная схема строгального станка с длинами звеньев ½ОА½=0,12м, ½АВ½=0,5 м, ½ВО₁½=0,4 м, ½ВС½=0,15 м, ½ДС½=0,5 м (рис. 4.1).

Рис. 4.1

Угловая скорость w₁=10 рад/с; погонная масса 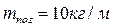; сила полезного сопротивления .

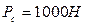Значения угловых скоростей и линейных скоростей выходного звена берем из кинематического анализа механизма.

Задание: определить момент инерции маховика методом Мерцалова.

Данный механизм в различные промежутки времени занимает различные положения (см. лист 1- кинематический анализ механизма). За цикл (который равен обороту кривошипа на угол ) выходное звено 5 совершает движение от нулевой точки (крайнего положения) до 4-ой (другого крайнего положения) и возвращается опять в нулевую точку. В зависимости от предназначения механизма движение выходного звена в одну сторону называется холостым, в другую - рабочим ходом. На протяжении рабочего хода на выходное звено действует сила (момент) полезного сопротивления.

В нашем механизме сила полезного сопротивления действует в промежутке 1-4, т. е. когда резец снимает стружку с детали, двигаясь справа налево. Значит, интервал 1-4 – интервал действия рабочей нагрузки, 4-0 – холостой ход.

Строим график действия силы сопротивления .

По оси абсцисс откладываем восемь отрезков, соответствующих восьми положениям механизма. По оси ординат откладываем значения силы полезного сопротивления в масштабе (рис. 4.2).

Рис. 4.2

Рассматривать реальный механизм при решении динамической задачи весьма проблематично, поскольку механизм представляет собой сложную систему. Поэтому реальный механизм заменим моделью. В качестве звена приведения возьмем начальное звено 1- кривошип (рис. 4.3).

Суммарный приведенный момент сил определяется по формуле:

(4.2)

где - приведенный момент движущих сил;

- приведенный момент от сил сопротивления.

Рис. 4.3

Приводим силу полезного сопротивления к начальному звену на основании равенства работ сил для модели и реального механизма. Запишем баланс работ

или

Разделим все на величину

.

Зная, что , а ,

получаем формулу

(4.3)

Для интервала рабочего хода

Для интервала холостого хода

Согласно уравнению (4.3) строим график приведенного момента от сил сопротивления (рис. 4.4).

Рис. 4.4

На графике необходимо подписывать все величины и масштабы.

При установившемся режиме работы механизма работа движущих сил за цикл равна работе сил сопротивления за цикл, т. е. для нашей модели

(4.4)

где - работа приведенных движущих сил;

- работа приведенных сил сопротивления.

Представим уравнение (4.4) в виде

(4.5)

Для дальнейшего решения задачи воспользуемся двумя обстоятельствами:

1) кинематический цикл модели равен полному обороту кривошипа , т. е. .

2) В большинстве случаев значение движущего момента не изменится на протяжении всего цикла, т. е. .

Определяем из уравнения (4.5)

(4.6)

Интеграл, стоящий в числителе, вычислим геометрически.

По формуле (4.6) вычислим

Строим график (рис. 4.5). Учитываем, что движущие характеристики имеют положительный знак, действуют на протяжении всего цикла.

Рис. 4.5

Определяем значения суммарного приведенного момента по формуле (4.2):

Четвертая точка переходная, рассматриваем ее слева и справа.

Слева

Справа

По полученным данным строим график (рис. 4.6).

Рис. 4.6

По методу Мерцалова разобъём звенья механизма на две группы. К І-й группе отнесем звенья, приведенный момент инерции которых имеет постоянное значение. Это начальное звено и маховик. Ко ІІ-й группе- звенья, приведенный момент инерции которых имеет переменное значение. Это звенья 2, 3, 4 и 5.

Приведенный суммарный момент инерции

(4.7)

Определим величину для звеньев 2-5, пользуясь балансом кинетической энергии модели и реального механизма:

Кинетическая энергия для модели

Отсюда,

(4.8)

Находим значения для 8-и точек

.

В курсовом проекте необходимо в формулы подставлять значения.

По найденным значениям строим график приведенного момента инерции для ІІ-й группы (рис. 4.7).

Рис. 4.7

Приведенный момент инерции для І группы:

(4.9)

определить нельзя, так как неизвестны параметры маховика. Для решения задачи необходимо записать уравнение движения, которое основано на теореме об изменении кинетической энергии

(4.10)

где Т_нач- кинетическая энергия системы в начальный момент времени,

Т- кинетическая энергия системы в последующий момент времени,

- сумма работ всех характеристик для системы.

Кинетическую энергию разобьем на 2 группы Т_І и Т_ІІ, тогда уравнению движения можно придать вид

(4.11)

Зная Т_І, можно определить

Однако по методу Мерцалова необходимо знать не само значение , а перепад между его максимальным и минимальным значениями, т. е.

(4.12)

Учтем, что , .

Из формулы (4.12) определяем значение

(4.13)

что позволит определить параметры проектируемого маховика.

Неизвестную величину определим из уравнения (4.11). Так как нам необходимо знать не саму величину , а ее перепад, т. е. разницу между наибольшим и наименьшим ее значениями, определять не требуется (при вычитании она аннулируется).

Суммарная работа равна

(4.14)

Интеграл в уравнении (4.14) будем вычислять графически, тогда работа в той точке будет определяться выражением

(4.15),

где - площадь, ограниченная графиком суммарного момента, осью абсцисс в пределах от 0 до той точки.

По полученным данным строим график суммарной работы (рис. 4.8).

Рис. 4.8

Кинетическую энергию можно определить по формуле:

(4.16)

где - приведенный момент инерции ІІ группы звеньев.

Вычисляем значения

По полученным данным строим график (рис. 4.9).

Рис. 4.9

По формуле (4.11) строим график кинетической энергии І группы звеньев (рис. 4.10).

Рис. 4.10

Находим

Момент инерции начального звена

Момент инерции маховика

4.2 Определение геометрических размеров маховика

Принимаем конструкцию маховика, в котором основная масса сосредоточена на ободе (рис. 4.11).

Рис. 4.11

Обод 1 крепится спицами 2 к ступице 3.

Момент инерции маховика

(4.17)

Объем обода

(4.18)

Относительные коэффициенты:

;

; (4.19)

Отсюда

Тогда из последней формулы диаметр обода

, м (4.20)

где (соответствует плотности чугуна).

Определяем ширину обода и высоту обода .

Наружный диаметр обода

Внутренний диаметр обода

Диаметр вала под маховик рассчитывается из условия прочности на кручение:

(4.21)

где - максимальный приведенный момент от сил сопротивления;

=15…20 МПа.

Диаметр ступицы

Длина ступицы

Масса маховика

.

Маховик вычерчиваем на листе № 3 рядом с графиками, по которым определялся момент инерции маховика.