Задания для самостоятельной работы. 1.1.1.1. Оценки коэффициентов однофакторной регрессионной модели

К Л А С С И Ч Е С К И Й

Р Е Г Р Е С С И О Н Н Ы Й А Н А Л И З

ОДНОФАКТОРНАЯ РЕГРЕССИЯ

Расчетные формулы

1.1.1.1. Оценки коэффициентов однофакторной регрессионной модели

, ,

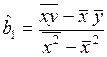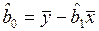где

, , , ,

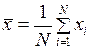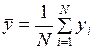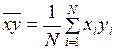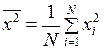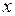– независимая переменная, 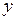– зависимая переменная, 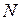– число элементов выборочной совокупности.

1.1.1.2. Коэффициент корреляции

,

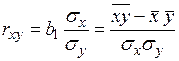где 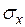, 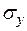– среднеквадратические ошибки, вычисляемые по формулам

, .

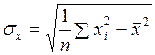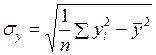1.1.1.3. Коэффициент детерминации

.

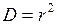1.1.1.4. Дисперсионное отношение Фишера (F-критерий)

,

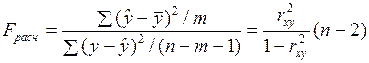где 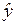– расчетное значение зависимой переменной (например, для случая линейной однофакторной модели 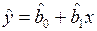), 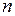– число элементов выборочной совокупности, 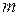– число факторов.

1.1.1.5. Стандартные ошибки параметров линейной регрессии

, ,

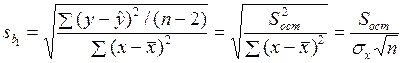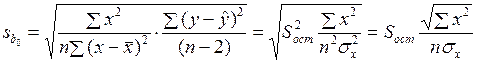где 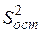– остаточная дисперсия, рассчитываемая по формуле

.

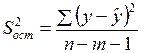1.1.1.6. t-статистики Стьюдента

, .

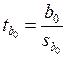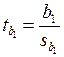1.1.1.7. Доверительные интервалы для коэффициентов регрессии

, ,

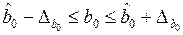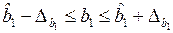где 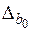, 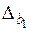– предельные ошибки, рассчитываемые по формулам

, ,

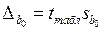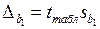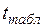– табличное значение t-статистики.

1.1.1.8. Индекс корреляции

.

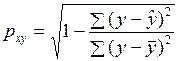1.1.1.9. Усредненное значение коэффициента эластичности

.

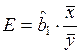1.1.1.10. Доверительные интервалы прогноза

,

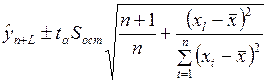где 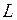– период упреждения, .

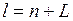Решение типовой задачи

Задание 1.1.2.1.ОАО «ЮВЖД» вынуждено периодически повышать цены на свои услуги. То, что повышение цен явно негативным образом влияет на число пассажиров, пользующихся услугами железной дороги, можно понять, проанализировав, в частности, данные табл. 1.1.2.1.

Т а б л и ц а 1.1.2.1

Стоимость проезда 1 чел. в поезде Воронеж - Москва, руб.	Среднемесячное число пассажиров поезда Воронеж-Москва	Стоимость проезда 1 чел. в поезде Воронеж - Москва, руб.	Среднемесячное число пассажиров поезда Воронеж-Москва

Несмотря на это, руководство «ЮВЖД» планирует в следующем периоде поднять цены на билеты для пассажиров поезда Воронеж – Москва. В связи с этим было решено поручить студенту экономического факультета, проходящего практику в отделе экономического анализа управления юго-восточной железной дороги, известным ему методом спрогнозировать среднемесячное число пассажиров поезда при условии, что билет на этот поезд будет стоить 690 руб. Студент-практикант решил применить к имеющимся данным регрессионный анализ и, воспользовавшись его результатами, получить требуемую прогнозную оценку.

Решение с помощью MS Excel

1. Ввод исходных данных.

2. Подготовка данных для расчета оценок коэффициентов линейной регрессии и оформление их в виде табл. 1.1.2.2.

Т а б л и ц а 1.1.2.2

№ п.п.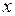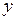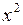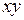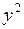
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
Средние значения	416,88	10918,13	205268,75	4349625,00	120652931,25

3. Расчет оценок коэффициентов регрессии

, .

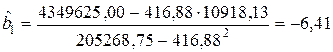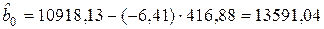Таким образом, построенная модель может быть записана в виде

.

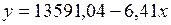Коэффициент 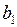этой модели показывает, что в среднем увеличение стоимости проезда на 1 руб. приводит к уменьшению числа пассажиров на 6 человек.

4. Расчет коэффициентов корреляции и детерминации

; ;

; .

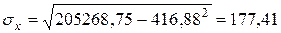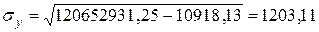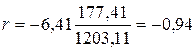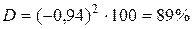Коэффициент корреляции достаточно высокий, что свидетельствует о существенной зависимости среднемесячного числа пассажиров от стоимости проезда. Коэффициент детерминации также достаточно высокий, он показывает, что число пассажиров объясняется стоимостью проезда на 89%.

5. Расчет дисперсионного отношения Фишера

.

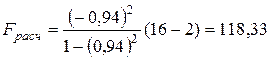Сравнение расчетного значения F-критерия с табличным 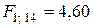для 95%-го уровня значимости (см. Приложение) позволяет сделать вывод об адекватности построенной модели.

6. Расчет стандартных ошибок по формулам (1.1.1.5), в которых используется средняя квадратическая ошибка 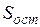, вычисленная в соответствии с данными табл. 1.1.2.3.

Т а б л и ц а 1.1.2.3

№ п.п.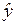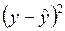
1.			12436,92	2201,04
2.			12436,92	26596,64
3.			12116,33	42570,52
4.			12116,33	31090,95
5.			12116,33	287645,85
6.			11378,97	123220,91
7.			11378,97	12327,30
8.			11378,97	442,19
9.			10641,62	669750,71
10.			10641,62	135706,02
11.			10641,62	467,30
12.			9904,26	45908,38
13.			9904,26	155442,84
14.			9198,97	450285,72
15.			9198,97	83501,74
16.			9198,97	383119,74
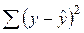		2450277,85
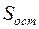	418,35

, .

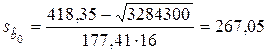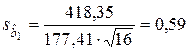7. Расчет t-статистик Стьюдента

, .

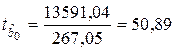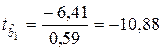Сравнение расчетных значений с табличным 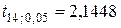(см. Приложение) подтверждает значимость коэффициентов регрессии.

8. Расчет доверительных границ для коэффициентов регрессии

, ,

; ;

; .

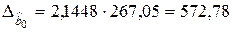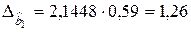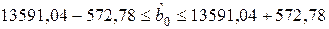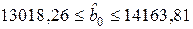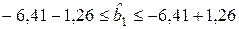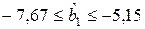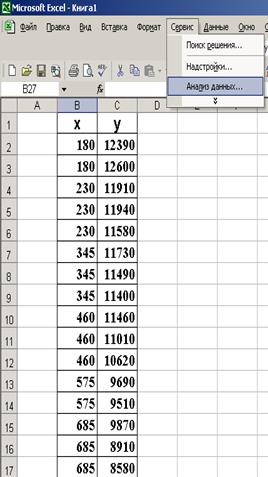
9. Построение линейного уравнения регрессии и расчет всех его характеристик с помощью пакета «Анализ данных» Excel. Для этого сначала необходимо проверить доступ к пакету анализа (см. рис. 1.1.2.1), а затем выполнить действия по построению регрессионного уравнения (см. рис. 1.1.2.2). Результат применения инструмента «Регрессия» представлен на рис. 1.1.2.3.

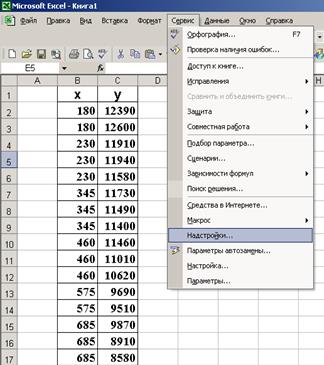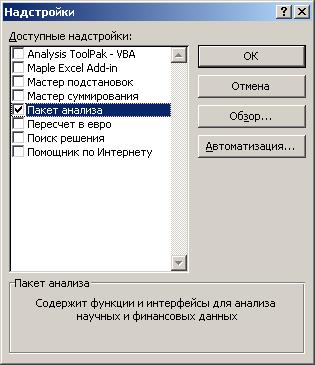Р и с. 1.1.2.1. Подключение надстройки Пакет анализа

10. Получение прогнозной оценки числа пассажиров

.

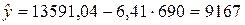11. Расчет доверительных границ прогнозной оценки

,

.

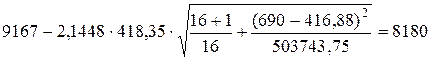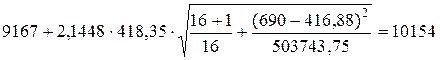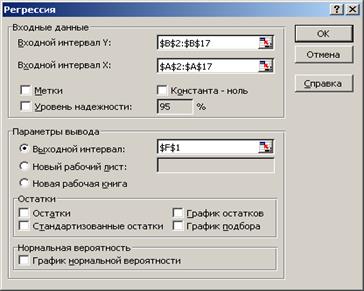Р и с. 1.1.2.2. Построение регрессионного уравнения

с помощью пакета «Анализ данных» MS Excel

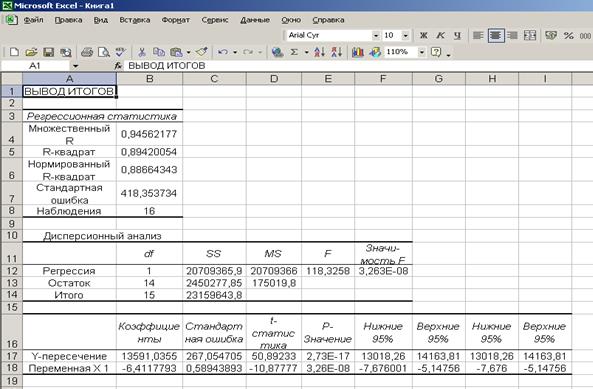
Р и с. 1.1.2.3. Результат применения инструмента «Регрессия»

Задания для самостоятельной работы

Задание 1.1.3.1. Начальник отдела маркетинга кинотеатра «Отражение» поручил своим сотрудникам провести исследование, в результате которого необходимо: 1) выявить фактор, в наибольшей степени влияющий на среднее число зрителей за первые три дня проката фильма; 2) построить прогнозную модель в виде линейной функции; 3) с помощью построенной модели получить прогнозные оценки среднего числа зрителей на первые три дня проката следующих двух фильмов. Специалисты отдела маркетинга экспертным путем в качестве фактора, в наибольшей степени влияющего на посещение киносеансов, установили расходы на рекламу фильма, (см. табл. 1.1.3.1). Выполните 2-е и 3-е задание начальника отдела маркетинга.

Т а б л и ц а 1.1.3.1

Среднее число зрителей за первые три дня проката фильма	Расходы на рекламу фильма, руб.	Среднее число зрителей за первые три дня проката фильма	Расходы на рекламу фильма, руб.

Задание 1.1.3.2. В табл. 1.1.3.2 представлены данные, которые были собраны при проведении исследований по оценке стоимости недвижимости.

Т а б л и ц а 1.1.3.2

Дом	Оценка инвентаризации, тыс. у.е.	Рыночная стоимость, тыс. у.е.	Дом	Оценка инвентаризации, тыс. у.е.	Рыночная стоимость, тыс. у.е.
	68,2	87,4		74,0	88,4
	74,6	88,0		72,8	93,6
	64,6	87,2		80,4	92,8
	80,2	94,0		74,2	90,6
	76,0	94,2		80,0	91,6
	78,0	93,6		81,6	92,8
	76,0	88,4		75,6	89,0
	77,0	92,2		79,4	91,8
	75,2	90,4		82,2	98,4
	72,4	90,4		67,0	89,8
	80,0	93,6		72,0	97,2
	76,4	91,4		73,6	95,2
	70,2	89,6		71,4	88,8
	75,8	91,8		81,0	97,4
	79,2	94,8		80,6	95,4

Построить регрессионное уравнение, отражающее зависимость рыночной стоимости дома от стоимости, указанной в книге инвентаризации.

Для построенного уравнения вычислить:

1) коэффициент корреляции; 2) коэффициент детерминации; 3) дисперсионное отношение Фишера; 3) стандартные ошибки коэффициентов регрессии; 4) t-статистики Стьюдента; 5) доверительные границы коэффициентов регрессии; 6) усредненное значение коэффициента эластичности.

Рассчитайте рыночную стоимость дома, если инвентаризационная комиссия оценит его в 90,5 тыс. у.е.

Все расчеты проведите в Excel с использованием выше приведенных формул и пакета анализа. Результаты, полученные по формулам и с помощью пакета анализа, сравните между собой.

Задание 1.1.3.3. По данным табл. 1.1.3.2 постройте уравнение регрессии в виде показательной функции. Для построенного уравнения вычислите:

1) индекс корреляции; 2) коэффициент детерминации; 3) F-критерий.

Дайте содержательную интерпретацию коэффициента регрессии, построенной модели. Все расчеты проведите в Excel с использованием выше приведенных формул.

Задание 1.1.3.4. По данным табл. 1.1.3.3:

1) для характеристики зависимости стоимости поддержанных автомобилей ВАЗ 2105 и ВАЗ 2107 рассчитайте параметры функций равносторонней гиперболы;

2) постройте степенные уравнения регрессии, отражающие зависимость стоимости подержанных автомобилей моделей ВАЗ 2109 и ВАЗ 21099 от срока их эксплуатации. Для построенных уравнений вычислите: а) индекс корреляции; б) коэффициент детерминации; в) дисперсионное отношение Фишера. Дайте содержательную интерпретацию коэффициента регрессии, построенных моделей.

Т а б л и ц а 1.1.3.3

Стоимость подержанных автомобилей, руб.	Срок эксплуатации, лет
ВАЗ 2105	ВАЗ 2107	ВАЗ 2109	ВАЗ 21099

Задание 1.1.3.5. Данные о доходностях рискованных активов трех видов, доходностях рыночного индекса акций и величинах безрисковой процентной ставки последовательно за 12 мес. приведены в табл. 1.1.3.4. Оцените коэффициенты линейных регрессий 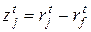, 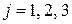по 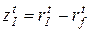и найдите значения всех показателей, используемых для тестирования моделей.

Т а б л и ц а 1.1.3.4