Основные правила дифференцирования элементарных функций.
1. Если 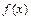 и
и 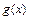 дифференцируемые функции,
дифференцируемые функции, 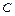 - постоянная, то:
- постоянная, то:
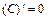 | 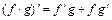 |
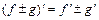 | 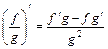 , , 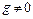 |
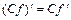 | 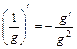 , , 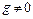 |
2.Если функция 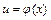 дифференцируема в точке
дифференцируема в точке 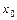 , а функция
, а функция 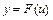 дифференцируема в точке
дифференцируема в точке 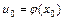 , то сложная функция
, то сложная функция 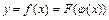 дифференцируема в точке
дифференцируема в точке 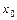 и имеет производную:
и имеет производную:
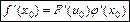 или кратко
или кратко 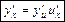 ..
..
При дифференцировании сложных функций для производной используют обозначения типа 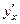 там, где необходимо уточнить, по какой переменной ведётся дифференцирование.
там, где необходимо уточнить, по какой переменной ведётся дифференцирование.
Производной 2-ого порядкаот функции 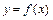 называется производная от её первой производной и обозначается
называется производная от её первой производной и обозначается 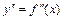 , т. е.
, т. е. 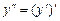 . В общем производной порядка
. В общем производной порядка 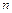 (
( 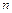 -ой производной)называется производная от
-ой производной)называется производная от 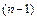 -ой производной и обозначается
-ой производной и обозначается 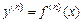 , т.е.
, т.е. 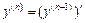 .Для производной
.Для производной 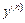 используется также обозначение
используется также обозначение 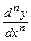 . Производная
. Производная 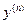 функции
функции  вычисляется её последовательным дифференцированием:
вычисляется её последовательным дифференцированием: 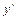 ,
, 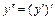 ,
, 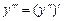 , …,
, …, 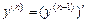 .
.
Дифференциалом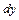 функции
функции  в точке
в точке 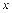 называется выражение
называется выражение 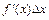 , т.е.
, т.е. 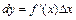 . В частности, для функции
. В частности, для функции 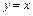 имеем
имеем 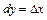 , т.е. дифференциал независимого переменного
, т.е. дифференциал независимого переменного 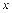 совпадает с приращением
совпадает с приращением 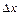 . Поэтому дифференциал функции
. Поэтому дифференциал функции  записывается в виде
записывается в виде 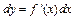 .
.
Дифференциалом 2-ого порядкафункции 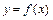 называется дифференциал от её первого дифференциала и обозначается
называется дифференциал от её первого дифференциала и обозначается 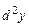 , т. е.
, т. е. 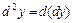 . В общем дифференциалом порядка
. В общем дифференциалом порядка 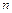 называется дифференциал от дифференциала
называется дифференциал от дифференциала 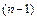 -ого порядка и обозначается
-ого порядка и обозначается 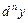 , т.е.
, т.е. 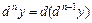 .
.
Если 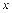 - независимая переменная, то для нахождения дифференциала
- независимая переменная, то для нахождения дифференциала 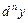 функции
функции 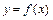 справедлива формула
справедлива формула 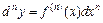 .
.
Первый дифференциал применяют для приближённого вычисления значений функции  в малой окрестности точки
в малой окрестности точки 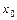 , в которой функция дифференцируема, по формуле:
, в которой функция дифференцируема, по формуле:
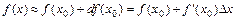 , где
, где 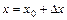 .
.
Чем меньше значение 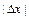 , тем точнее приближённая формула.
, тем точнее приближённая формула.
Частной производной (1-ого порядка) функции 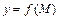 в точке
в точке 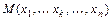 по переменной
по переменной 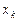 называется предел
называется предел 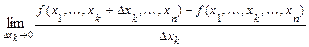 , если этот предел существует. Частную производную обозначают
, если этот предел существует. Частную производную обозначают 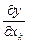 или
или 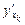 .
.
Частные производные вычисляются по обычным правилам дифференцирования функции одной переменной, в предположении, что все аргументы функции, кроме аргумента 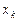 , по которому берётся производная, постоянны.
, по которому берётся производная, постоянны.
Частными производными второго порядка функции 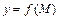 называются частные производные от её частных производных первого порядка. При этом используются обозначения:
называются частные производные от её частных производных первого порядка. При этом используются обозначения:
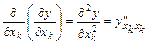 ,
, 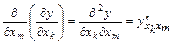 (
( 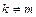 ).
).
Производные 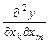 (
( 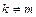 ) называются смешанными. Аналогично определяются и обозначаются частные производные порядка выше второго. Для функции
) называются смешанными. Аналогично определяются и обозначаются частные производные порядка выше второго. Для функции 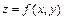 частные производные обозначаются:
частные производные обозначаются:
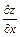 ,
, 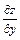 ,
, 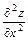 ,
, 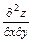 ,
, 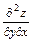 ,
, 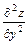 ,… или
,… или 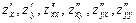 ,….
,….
Если смешанные частные производные, подлежащие вычислению, непрерывны, то результат многократного дифференцирования функции по различным переменным не зависит от порядка дифференцирования.
Полным дифференциалом 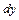 функции
функции 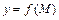 в точке
в точке 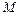 называется выражение вида
называется выражение вида 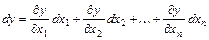 , где
, где 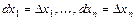 .
.
Дифференциалом 2-ого порядкафункции 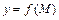 называется дифференциал от её первого дифференциала и обозначается
называется дифференциал от её первого дифференциала и обозначается 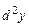 , т. е.
, т. е. 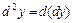 . В общем дифференциалом порядка
. В общем дифференциалом порядка 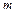 называется дифференциал от дифференциала
называется дифференциал от дифференциала 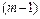 -ого порядка и обозначается
-ого порядка и обозначается 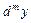 , т.е.
, т.е. 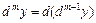 .
.
Для функции 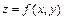 справедливы формулы:
справедливы формулы:
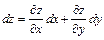 ,
, 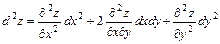 .
.
Первый дифференциал применяют для приближённого вычисления значений функции 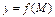 в малой окрестности точки
в малой окрестности точки 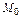 , в которой функция дифференцируема, по формуле:
, в которой функция дифференцируема, по формуле: 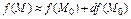 . В частности, для функции
. В частности, для функции 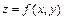 по формуле:
по формуле: 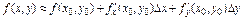 , где
, где 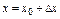 ,
, 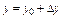 . Чем меньше значение
. Чем меньше значение 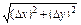 , тем точнее формула.
, тем точнее формула.
Тема 9. Исследование функций с помощью производных, построение их графиков.
Уравнение касательной к графику функции 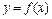 в точке
в точке 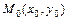 имеет вид:
имеет вид: 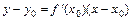 ,
,
уравнение нормали - вид: 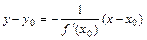 .
.
Правило Лопиталя. Предел отношения двух дифференцируемых или бесконечно малых или бесконечно больших функций при 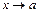 (
( 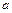 - число
- число 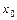 или символ
или символ 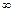 ) равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле:
) равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле:
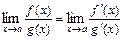 .
.
Правило Лопиталя используют для раскрытия неопределённостей видов 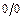 и
и 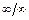 . На каждом этапе применения правила Лопиталя следует пользоваться упрощающими отношение тождественными преобразованиями, а также комбинировать это правило с любыми другими приёмами вычисления пределов. В некоторых случаях может потребоваться неоднократное применение данного правила.
. На каждом этапе применения правила Лопиталя следует пользоваться упрощающими отношение тождественными преобразованиями, а также комбинировать это правило с любыми другими приёмами вычисления пределов. В некоторых случаях может потребоваться неоднократное применение данного правила.
Раскрытие неопределённостей видов 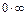 ,
, 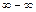 путём преобразований:
путём преобразований:
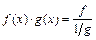 ,
, 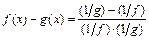
приводится к раскрытию неопределенностей видов 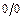 и
и 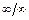 .
.
Функция  называется возрастающей (убывающей) на интервале
называется возрастающей (убывающей) на интервале 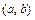 , если для любых
, если для любых 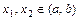 , удовлетворяющих условию
, удовлетворяющих условию 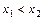 , выполняется неравенство
, выполняется неравенство 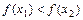 (
( 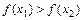 ).
).
Если функция 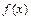 дифференцируема на интервале
дифференцируема на интервале 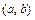 и
и 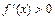 (
( 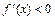 ) при всех
) при всех 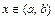 , то функция
, то функция 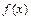 возрастает (убывает) на
возрастает (убывает) на 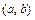 .
.
Точка 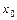 , принадлежащая области определения
, принадлежащая области определения 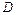 функции
функции  , называется критической точкойфункции, если в этой точке
, называется критической точкойфункции, если в этой точке 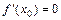 или
или 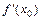 не существует. Критические точки функции
не существует. Критические точки функции  разбивают её область определения
разбивают её область определения 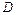 на интервалы монотонности (интервалы возрастания и убывания).
на интервалы монотонности (интервалы возрастания и убывания).
Точка 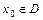 называется точкой минимума (максимума) функции
называется точкой минимума (максимума) функции  , если существует окрестность точки
, если существует окрестность точки 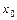 такая, что для всех точек
такая, что для всех точек 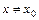 этой окрестности выполняется неравенство
этой окрестности выполняется неравенство 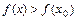 (
( 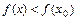 ), а число
), а число 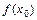 - минимумом (максимумом) функции. Точки минимума и максимума функции называются точками экстремума, а значения функции в этих точках – экстремумами функции.
- минимумом (максимумом) функции. Точки минимума и максимума функции называются точками экстремума, а значения функции в этих точках – экстремумами функции.
Необходимое условие экстремума.Если 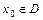 - точка экстремума функции
- точка экстремума функции  , то
, то 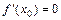 или
или 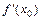 не существует.
не существует.
Достаточное условие экстремума. Пустьфункция  дифференцируема в окрестности точки
дифференцируема в окрестности точки 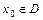 , в которой
, в которой 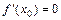 или
или 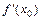 не существует. Тогда, если производная
не существует. Тогда, если производная 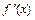 , при переходе слева направо через точку
, при переходе слева направо через точку 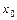 : 1) меняет знак с «+» на «
: 1) меняет знак с «+» на « 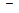 », то
», то 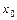 - точка максимума; 2) меняет знак с знак с «
- точка максимума; 2) меняет знак с знак с « 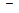 » на «+», то
» на «+», то 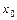 - точка минимума; 3) сохраняет знак, то
- точка минимума; 3) сохраняет знак, то 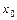 не является точкой экстремума.
не является точкой экстремума.
Наибольшее и наименьшее значения функции 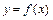 непрерывной и кусочно-дифференцируемой (дифференцируемой, за исключением, быть может, конечного числа точек) на отрезке
непрерывной и кусочно-дифференцируемой (дифференцируемой, за исключением, быть может, конечного числа точек) на отрезке 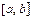 достигается или во внутренних критических точках или на концах отрезка.
достигается или во внутренних критических точках или на концах отрезка.
Функция 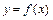 называется выпуклой (вогнутой) на интервале
называется выпуклой (вогнутой) на интервале 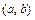 , если её график лежит под касательной (над касательной), проведённой к графику данной функции, в любой точке интервала
, если её график лежит под касательной (над касательной), проведённой к графику данной функции, в любой точке интервала 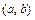 .
.
Если функция 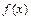 дважды дифференцируема на интервале
дважды дифференцируема на интервале 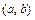 и
и 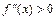 (
( 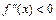 ) при всех
) при всех 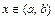 , то функция является вогнутой (выпуклой) на
, то функция является вогнутой (выпуклой) на 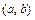 .
.
Точка 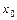 , принадлежащая области определения
, принадлежащая области определения 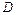 функции
функции  , называется точкой перегибафункции, если при переходе через неё меняется направление выпуклости функции. Точка
, называется точкой перегибафункции, если при переходе через неё меняется направление выпуклости функции. Точка 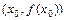 при этом называется точкой перегиба графика функции.
при этом называется точкой перегиба графика функции.
Точка 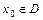 называется точкой возможного перегибафункции
называется точкой возможного перегибафункции  , если в этой точке
, если в этой точке 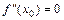 или
или 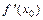 не существует. Эти точки разбивают область определения
не существует. Эти точки разбивают область определения 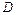 функции
функции  на интервалы выпуклости и вогнутости.
на интервалы выпуклости и вогнутости.
Необходимое условие перегиба.Если 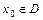 - точка перегиба функции
- точка перегиба функции  , то
, то 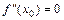 или
или 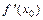 не существует.
не существует.
Достаточное условие перегиба.Пустьфункция  дважды дифференцируема в окрестности точки
дважды дифференцируема в окрестности точки 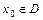 , в которой
, в которой 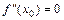 или
или 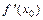 не существует. Тогда, если производная
не существует. Тогда, если производная 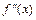 , при переходе через точку
, при переходе через точку 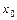 меняет знак, то
меняет знак, то 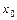 - точка перегиба.
- точка перегиба.
Для построения графика функции  нужно:
нужно:
1) найти область определения функции;
2) найти область непрерывности функции и точки разрыва;
3) исследовать функцию на чётность, нечётность и периодичность;
4) найти точки пересечения графика с осями координат;
5) найти асимптоты графика функции;
6) найти интервалы возрастания и убывания, экстремумы функции;
7) найти интервалы выпуклости, вогнутости и точки перегиба.
Точка 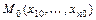 , принадлежащая области определения
, принадлежащая области определения 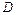 функции
функции 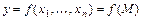 , называется стационарной точкойфункции, если в этой точке каждая из её частных производных равна нулю, т.е.
, называется стационарной точкойфункции, если в этой точке каждая из её частных производных равна нулю, т.е. 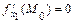 ,…,
,…, 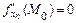 или
или 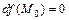 .
.
Точка 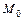 называется точкой минимума (максимума) функции
называется точкой минимума (максимума) функции 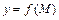 , если существует окрестность точки
, если существует окрестность точки 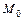 такая, что для всех точек
такая, что для всех точек 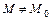 этой окрестности выполняется неравенство
этой окрестности выполняется неравенство 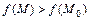 (
( 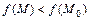 ).
).
Точки минимума и максимума функции называются точками экстремума, а значения функции в этих точках – экстремумами функции.
Необходимое условие экстремума. Если 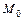 - точка локального экстремума функции
- точка локального экстремума функции 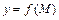 , дифференцируемой в точке
, дифференцируемой в точке 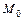 , то
, то 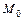 - стационарная точка функции.
- стационарная точка функции.
Достаточное условие экстремума. Пусть 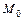 - стационарная точка дважды дифференцируемой в точке
- стационарная точка дважды дифференцируемой в точке 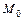 функции
функции 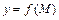 . Тогда, если при всевозможных наборах значений
. Тогда, если при всевозможных наборах значений 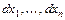 , не равных одновременно нулю:
, не равных одновременно нулю:
1) 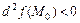 , то в точке
, то в точке 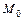 функция
функция 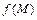 имеет максимум; 2)
имеет максимум; 2) 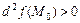 , то в точке
, то в точке 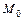 функция имеет минимум; 3)
функция имеет минимум; 3) 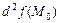 принимает как положительные, так и отрицательные значения, то в точке
принимает как положительные, так и отрицательные значения, то в точке 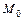 функция
функция 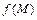 не имеет экстремума.
не имеет экстремума.
В частности, функция 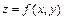 в стационарной точке
в стационарной точке 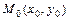 , при условии
, при условии 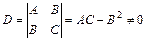 , где
, где 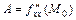 ,
, 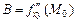 ,
, 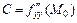 : 1) имеет максимум, если
: 1) имеет максимум, если 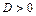 и
и 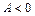 ; 2) имеет минимум, если
; 2) имеет минимум, если 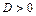 и
и 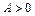 ; 3) не имеет экстремума, если
; 3) не имеет экстремума, если 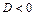 .
.
