Основные правила дифференцирования функций одной переменной (одно из этих правил доказать)
Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему).
Понятие дифференцируемости функции
Определение.Функция y=f(x) называется дифференцируемой в точке х, если ее приращение Δу в этой точке можно представить в виде
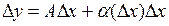 ,
,
где А – некоторое число, не зависящее от 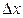 , а α(
, а α( 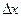 ) – функция аргумента
) – функция аргумента 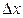 , являющаяся бесконечно малой при
, являющаяся бесконечно малой при 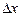 →0, т.е.
→0, т.е. 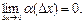
Выясним теперь связь между дифференцируемостью в точке и существованием производной в той же точке.
Теорема. Для того чтобы функция f(x) была дифференцируемой в данной точке х , необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Связь между дифференцируемостью функции и ее непрерывностью
Пример. Доказать, что функция y=│х│ недифференцируема в точке х=0 .
Решение. Производная функции (если она существует) равна
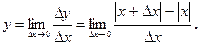
Очевидно, что при х=0 производная не существует, так как отношение 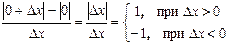 , т.е. не имеет предела при Δх→0 (ни конечного, ни бесконечного). Геометрически это означает отсутствие касательной к кривой в точке х=0.
, т.е. не имеет предела при Δх→0 (ни конечного, ни бесконечного). Геометрически это означает отсутствие касательной к кривой в точке х=0.
Теорема. Если функция y=f(x) дифференцируема в точке х0,, то она в этой точке непрерывна.
□Доказательство.По условия функция y=f(x) дифференцируема в точке х0, т.е. существует конечный предел
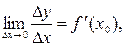
где f′(x0) – постоянная величина, не зависящая от 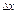 .
.
Тогда на основании теоремы о связи бесконечно малых величин с пределами функций можно записать
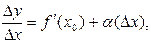
где α(∆х) является бесконечно малой величиной при 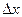 →0, или
→0, или
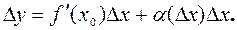 .
.
При Δх→0 на основании свойств бесконечно малых величин устанавливаем, что Δу→0 и, следовательно, по определению непрерывности функции в точке, делаем вывод, что функция непрерывна в токе х0. ■
Обратная теорема, вообще говоря, неверна, если функция непрерывна в данной точке, то она не обязательно дифференцируема в этой точке. Так, функция y=│х│ непрерывна в точке х0=0, ибо 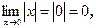 но, как было доказано ранее недифференцируема в этой точке.
но, как было доказано ранее недифференцируема в этой точке.
Таким образом, непрерывность функции – необходимое, но не достаточное условие ее дифференцируемости.
Замечание: Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором промежутке Х, то функция называется гладкой на этом промежутке. Если же производная функция допускает конечное число точек разрыва, то такая функция на данном промежутке называется кусочно гладкой.
Основные правила дифференцирования функций одной переменной (одно из этих правил доказать).
Производная функции 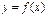 м.б. найдена по схеме:
м.б. найдена по схеме:
1) Дадим аргументу приращение 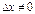 и найдем наращение значений функции
и найдем наращение значений функции 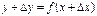 .
.
2) Находим приращение функции 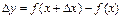 .
.
3) Составляем отношение 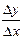 .
.
4) Находим предел этого отношения при 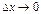 , т.е.
, т.е. 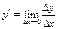 (если этот предел существует).
(если этот предел существует).
