Исчезновение тока при размыкании цепи

Пусть цепь состоит из катушки с индуктивностью L, резистора сопротивлением R, источника ЭДС и ключа К (рис.2.2). Когда ключ К находится в позиции 1, в цепи течет ток I = ξ /R (r<<R). В момент t = 0 ключ перебрасывается в позицию 2.

R

L

К

ξ

Ток в цепи начнет убывать и возникнет ЭДС самоиндукции, противодействующая убыванию тока. По закону Ома

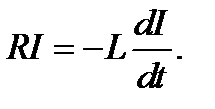(2.12)

Рис.2.2

При интегрировании уравне- ния по току от I₀ до I и по времени от 0 до t, получим

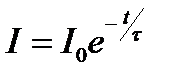. (2.13)

где t = L/R – постоянная времени, называемая временем релаксации. Зависимость I(t) представлена кривой 1 на рис.2.3.

Установление тока при замыкании цепи

В момент t = 0 ключ К повернем в позицию 1 и тем самым к индуктивности подключим источник ЭДС. Ток в цепи начнет нарастать и снова возникнет ЭДС самоиндукции. По закону Ома

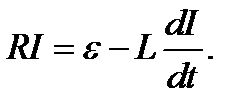(2.14)

Интегрируя по t уравнение (2.13), получим

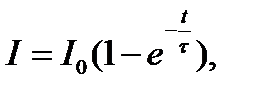(2.15)

t   t

I I0 0 0

Рис.2.3

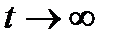где I₀ - установившийся ток (при ). График зависимости I(t) представлен кривой 2 на рис. 2.3.

Взаимная индукция

Взаимной индукцией называется возникновение ЭДС индукции в одном контуре при изменении тока в другом, если они расположены в непосредственной близости друг от друга (рис.2.4).

Рис.2.4

Очевидно, что магнитный поток, создаваемый в контуре 1 током, текущим в контуре 2, пропорционален току в контуре 2:

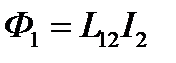. (2.16)

Аналогично, ток I₁ создаёт через контур 2 магнитный поток

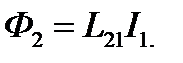(2.17)

Коэффициенты пропорциональности 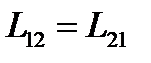называются коэффициентами взаимной индукции. Они зависят от геометрии обоих контуров и их взаимного расположения, а также от магнитной проницаемости среды. Можно доказать, что при отсутствии ферромагнетиков L₁₂ = L₂₁ .

Рассчитаем взаимную индукцию двух катушек, намотанных на общий тороидальный сердечник.

Если по первой катушке идёт ток I₁, то то магнитная индукция поля и магнитный поток этого тока в сердечнике тороида можно найти по формулам

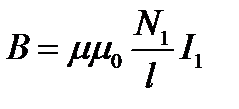, (2.18)

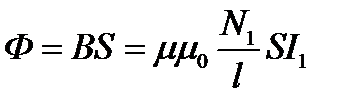, (2.19)

где l – длина средней линии тороида, N₁ – число витков первой катушки, S – площадь сердечника.

Полный магнитный поток через вторичную обмотку, содержа- щую N₂ витков

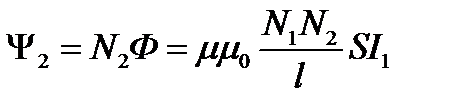. (2.20)

Согласно (2.17)

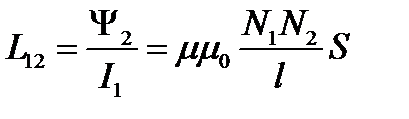. (2.21)

Если µ не зависит от силы тока, то

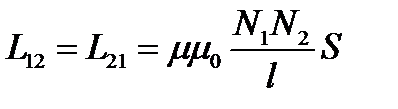. (2.22)

На явлении взаимной индукции основано действие трансформаторов, служащих для повышения или понижения напряжения переменного тока.

Концы первичной обмотки трансформатора присоединяются к источнику переменного напряжения с ЭДС ξ₁. Возникающий переменный ток создаёт в сердечнике трансформатора переменный магнитный поток Ф, который пронизывает витки вторичной обмотки. Изменение этого потока вызывает во вторичной обмотке появление ЭДС взаимной индукции, а в первичной ЭДС самоиндукции.

По закону Ома для первичной обмотки

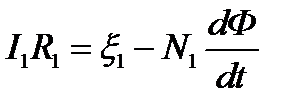. (2.23)

Пренебрегая падением напряжения на сопротивлении R₁, приближённо имеем

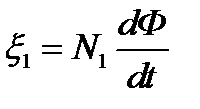. (2.24)

ЭДС взаимной индукции во вторичной обмотке

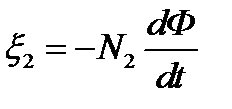. (2.25)

Из сопоставления выражений (2.24) и (2.25), получим

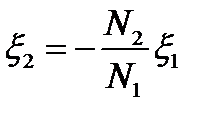, (2.26)

где знак минус показывает, что ЭДС в первичной и вторичной обмотках противоположны по фазе.

Отношение 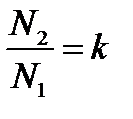, называется коэффициентом трансформации. Если κ >1, то трансформатор называется повышающим, если κ<1 – понижающий.

Энергия магнитного поля

Рассмотрим цепь, изображенную на рис.2.2. В положе- нии 1 ключа К в катушке установится ток, который обусловит магнитное поле. Если перебросить ключ в положение 2, то через сопротивление R будет некоторое время течь постепенно убывающий ток, поддерживаемый возникающей в катушке ЭДС самоиндукции. Работа, совершаемая этим током за время dt, равна

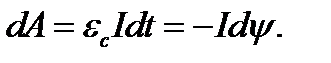(2.27)

Если индуктивность соленоида L=const, то

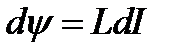и 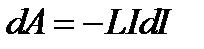. (2.28)

Интегрируя (2.28) от первоначального значения I до нуля, получим работу, совершаемую в цепи за все время,

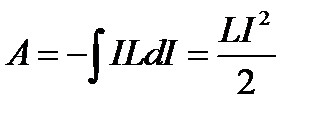. (2.29)

Данная работа совершается за счет убыли энергии магнитного поля, следовательно, энергия поля соленоида, через который течет ток I, равна

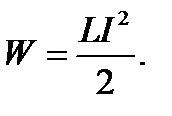(2.30)

Выразим энергию магнитного поля через величины, характеризующие само поле. Так как

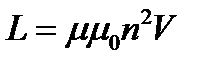и ,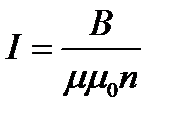

получим

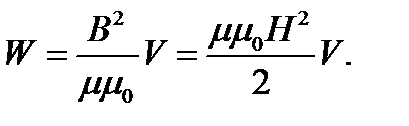(2.31)

Магнитное поле, а следовательно и его энергия, локализованы внутри соленоида. Отсюда для плотности энергии магнитного поля будем иметь

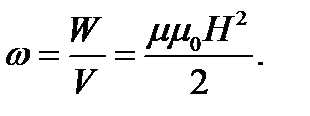(2.32)

Зная плотность энергии поля в каждой точке, можно путём интегрирования найти энергию поля, заключённого в любом объёме

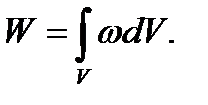(2.33)

2.6. Примеры решения задач по законам электромагнитной индукции

Пример 1. В однородном магнитном поле (В = 0,2Тл) равномерно с частотой ν = 600 мин^-1 вращается рамка, содержащая N = 1200 витков, плотно прилегающих друг к другу. Площадь рамки S = 100 см². Ось вращения лежит в плоскости рамки и перпендикулярна линиям магнитной индукции. Определите максимальную ЭДС, индуцируемую в рамке.

Решение

Согласно закону электромагнитной индукции

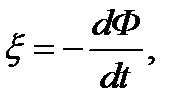
где Ф = NBScos α – полный магнитный поток, пронизывающий рамку.

ν

a

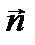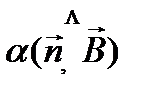При вращении рамки угол , образованный нормалью n к плоскости рамки и линиями индукции В, изменятся по закону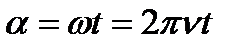

Подставив в закон электромагнит- ной индукции выражение магнит- ного потока и продифференцировав по времени, найдем мгновенное значение ЭДС индукции:

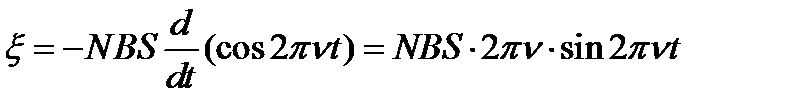
Максимальное значение ЭДС определится при условии, что sin 2πνt =1. таким образом,

.

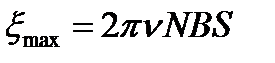Убедимся в том, что правая часть этого равенства дает единицу ЭДС (В):

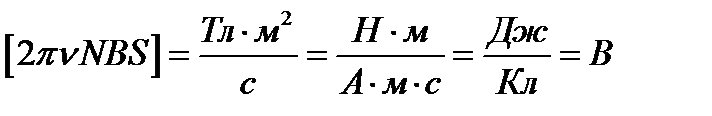
Произведем вычисление:

.

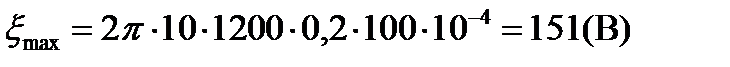Пример 2. Соленоид содержит N =1200 витков прово- да, плотно прилегающих друг к другу. При силе тока I = 4 A магнитный поток Ф = 6 мкВб. Определить индуктивность L соленоида и энергию магнитного поля соленоида.

Решение

Индуктивность L связана с потокосцеплением Ψ = LI.

Потокосцепление, в свою очередь, может быть определено через поток Ф и число витков N:

Ψ = NФ.

На основании этих формул индуктивность соленоида

.

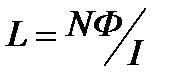Энергия магнитного поля соленоида

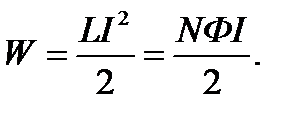
Подставим в формулы для L и W значения физических величин и произведем вычисления:

.

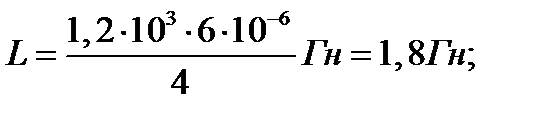
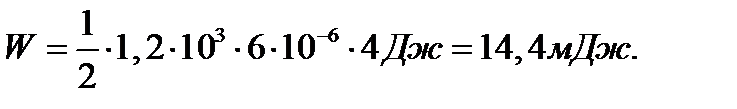Пример 3.Определить индукцию В и напряжённость Н магнитного поля на оси тороида без сердечника, по обмотке которого, содержащей N = 200 витков, идёт ток I =5 А. Внеш- ний диаметр d₁ тороида равен 30 см, внутренний d₂ = 20 см.

Решение

Для определения напряжённости магнитного поля внутри тороида вычислим циркуляцию вектора 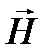вдоль линий магнитной индукции поля: .

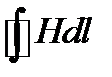Из условия симметрии следует, что линии магнитной индукции тороида представляют собой окружности и что во всех точках этой линии напряжённости одинаковы. Поэтому в выражении циркуляции напряжённость Н можно вынести за знак интеграла, а интегрирование проводить в пределах от нуля до 2πr, где r-радиус окружности, совпадающей с линией индукции, вдоль которой вычисляется циркуляция, т.е.

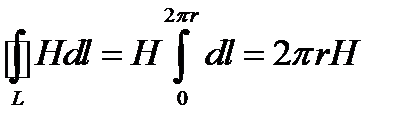. (1)

С другой стороны, в соответствии с законом полного тока циркуляция вектора напряжённости магнитного поля равна сумме токов, охватываемых контуром, вдоль которого вычисляется циркуляция:

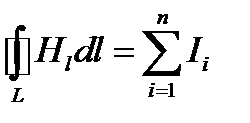. (2)

Приравняв правые части равенств (1) и (2) получим

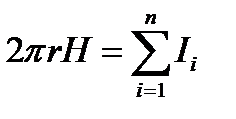. (3)

Линия, проходящая вдоль тороида, охватывает число токов, равное числу витков тороида. Сила тока во всех витках одинакова. Поэтому формула (3) примет вид 2πrН = Nl, откуда

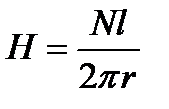. (4)

Для средней линии тороида r = (R₁+ R₂)/2= (d₁+ d₂)/4. Подставив выражение в формулу (4), найдём

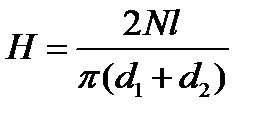. (5)

Магнитная индукция В₀ в вакууме связана с напряжённостью поля соотношением В₀=μ₀Н. Следовательно,

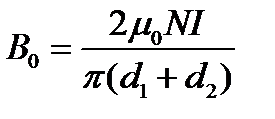. (6)

Подставив значения величин в выражения (5) и (6), получим: Н =1,37 кА/м, В₀ =1,6 мТл.

Пример 4. Чугунное кольцо имеет воздушный зазор длиной l₀ = 5мм. Длина l средней линии кольца равна 1 м. Сколько витков N содержит обмотка на кольце, если при силе тока I = 4А индукция В магнитного поля в воздушном зазоре равна 0,5 Тл. Рассеянием магнитного потока в воздушном зазоре можно пренебречь. Явление гистерезиса не учитывать.

Решение

Пренебрегая рассеянием магнитного потока, мы можем принять, что индукция поля в воздушном зазоре равна индукции поля в чугуне. На основании закона полного тока запишем: IN = Hl + H₀l_0. По графику (см. приложение6) находим что при B = 0,5 Тл, напряжённость Н магнитного поля в чугуне равна 1,2 кА/м. Так как для воздуха μ = 1, то напряжённость поля в воздушном зазоре 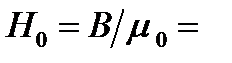0,4 МА/м. Искомое число витков N = (Hl+H₀l₀) / I = 800.