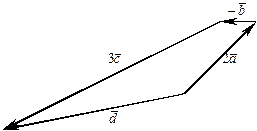Линейные операции над векторами

Кафедра высшей математики

Элементы векторной алгебры

Методические указания и контрольные задания для студентов первых курсов

всех специальностей очной формы обучения

Составители: Гуменникова Ю.В.,

Лаврусь О.Е.,

Самара

УДК 519.7

Элементы векторной алгебры : методические указания и контрольные задания по дисциплине «Высшая математика» для студентов первых курсов всех специальностей очной формы обучения / Ю.В. Гуменникова, О.Е. Лаврусь. – Самара: СамГУПС, 2010. – 44 с.

Утверждены на заседании кафедры 09.09.2010, протокол № 7.

Печатается по решению редакционно-издательского совета университета

Методические указания составлены в соответствии с Государственным образовательным стандартом, с действующей программой по высшей математике и охватывают основные разделы векторной алгебры.

В методических указаниях приведены индивидуальные задания, необходимые теоретические сведения, а также примеры решения задач.

Предназначены для студентов 1-го курса всех специальностей очной формы обучения.

Составители: Ю.В. Гуменникова, к.ф.-м.н., доцент,

О.Е. Лаврусь, к.т.н., доцент

Рецензенты: к. ф.-м. н., доцент СамГУ Воскресенская Л.А.

к. ф.-м. н., доцент СамГУПС Кайдалова Л.В..

Под редакцией зав. кафедрой «Высшая математика» Кузнецова В.П.

Компьютерная верстка

Подписано в печать ________ Формат 60х84. 1/16

Бумага писчая. Печать оперативная. Усл.п.л.

Тираж 300 экз. Заказ №

© Самарский государственный университет путей сообщения, 2010

Векторы

Вектором называется направленный отрезок. Если начало вектора находится в точке A, а конец в точке B, то вектор обозначается :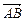

Если начало и конец вектора не указываются, то его обозначают строчной буквой латинского алфавита – 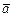, , 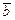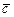и т.д:

Направление вектора изображается стрелкой. Через 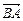обозначается вектор, направленный противоположно 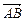, через 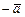вектор, направленный противоположно .

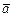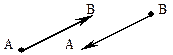
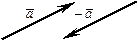
Вектор, у которого начало и конец совпадают, называется нулевым и обозначается .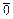

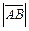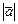Длиной, или модулем вектора, называется расстояние между его началом и концом. Записывается или , соответственно.

Векторы называются коллинеарными, если они параллельны одной прямой, и компланарными, если они параллельны одной плоскости.

Два вектора называются равными, если они коллинеарны, одинаково направлены и равны по длине.

Два вектора называются ортогональными, если они перпендикулярны друг другу.

Свободным вектором в пространстве называется вектор, который без изменения дины и направления может быть перенесен в любую точку пространства.

Линейные операции над векторами

К линейным операциям над векторами относятся: умножение вектора на число и сложение (вычитание) векторов.

Произведением вектора 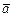на число m называется вектор 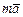, направление которого совпадает с направлением вектора 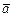, если m > 0 и противоположно ему, если m < 0. Длина вектора обозначается 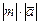или 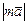. Например:

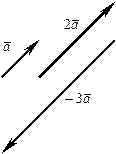
Сумму (разность) двух свободных векторов можно найти по правилу параллелограмма.

Пример. Даны свободные векторы 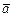и :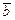

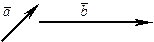
Поместим их начала в одну точку и достроим до параллелограмма:

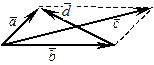
Тогда вектор 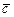= 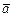+ 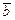направлен по диагонали, берущей начало из этой же точки, а вектор 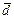= 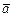– 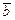будет направлен по другой диагонали параллелограмма от вычитаемого к уменьшаемому.◄

Если векторов больше двух, то применяют правило многоугольника, согласно которому векторы помещают последовательно (начало последующего помещается в конец предыдущего), а суммой векторов будет являться вектор, начало которого находится в начале первого вектора, а конец – в конце последнего вектора.

Пример. Даны векторы , , :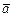

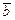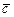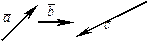
Найти линейную комбинацию .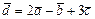

Решение. Найдем векторы 2 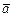, – , 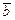3 :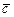

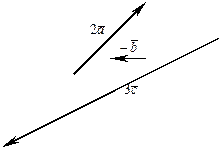
Применив правило многоугольника, получаем