Изучение явлений переноса в газах. Теплопроводность

Лабораторная работа № 2. 2.

Цель работы:определение коэффициента теплопроводности воздуха и микропараметров движения молекул методом нагреваемой нити.

I. Основные понятия и определения

Общее содержание явлений переноса заключается в выравнивании по объёму макроскопических пространственных неоднородностей плотности, энергии и импульса направленного движения молекул и их столкновений.

В отношении явления теплопроводности это означает, что наличие градиента температуры в объёме газа приводит к возникновению теплового потока, направленного в сторону уменьшения температуры. Макроскопическим уравнением теплопроводности является уравнение Фурье, которое можно представить в виде:

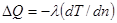. (1)

Здесь: 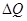– количество тепла, переносимого за единицу времени через единичную, перпендикулярную направлению переноса площадку, 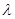– коэффициент теплопроводности, – градиент температуры в направлении нормали 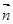к поверхности равной температуры. С макроскопической точки зрения явление теплопроводности обусловлено переносом энергии хаотического движения молекулами из области более высокой температуры за счёт хаотического движения в окружающее пространство и передачу её при столкновении молекулами с меньшей тепловой энергией (напомним, что средняя энергия теплового хаотического движения молекулы, 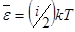, где i – число степеней свободы молекулы). Обратно, молекулы из окружающей среды, попадая в область более высокой температуры, отбирают энергию у молекул с большей энергией. Таким образом, температура без поддержания извне должна с течением времени выровняться по всему объёму газа.

Очевидно, что теплопроводность газа определяется, прежде всего, микропараметрами движения молекул: средней тепловой скоростью, средней длиной свободного пробега 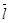, плотностью (концентрацией) газа. Действительно, как следует из теории, зависимость коэффициента теплопроводности от микропараметров даётся выражением вида:

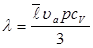. (2)

где: 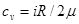– удельная теплоёмкость газа при постоянном объёме. Если поставить в выражение (2) значения 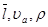согласно теории 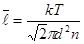, , 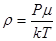, 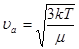R=kN_A, то получим выражение вида:

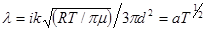. (3)

Следовательно, сравнение измеренного значения коэффициента теплопроводности и определенного из выражения (3) позволит оценить правильность результата измерений.

Также можно при известной связи между коэффициентами внутреннего трения и теплопроводности 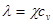, при известной удельной теплоёмкости воздуха с_v=0,723кДж/кг∙К, по измеренному значению коэффициента теплопроводности и формулам определить микропараметры движения молекул воздуха: d, 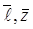. Перенос тепла в общем случае может осуществляться не только с помощью рассмотренного выше механизма теплопроводности, но и конвекцией и лучеиспусканием. При конвекции возникают перемещения микроскопических объемов газа, которые и переносит тепло. Она обычно проявляет себя в достаточно больших объёмах газа, при большей разности температур. Например, конвекция наглядна в мерцании изображения над большой нагретой поверхностью. При лучеиспускании энергия нагретого тела уносится излучаемыми им фотонами. При чём, согласно закону Стефана- Больцмана, энергия излучения пропорциональна площади нагретой поверхности и четвёртой степени её температуры. Поэтому механизм лучеиспускания важен для передачи тепла от сильно нагретых тел большой площади.

II. Методика эксперимента

Для изучения механизма теплопроводности целесообразно использовать метод нагретой нити, которой реализуется в данной работе. Нить, представляющая собой высокоомную проволоку и проходящая в середине массивной трубки, нагревается протекающим по ней током I от источника напряжения. При установлении процесса теплопередачи джоулево тепло Q₁=I²Rt, выделяющееся в объеме нити при протекании тока, уносится молекулами на стенки трубки согласно закону Фурье, который в нашем случае примет вид: Q₂=2πλtΔT∙ln(d₁/d₂), т.е. Q₁=Q₂. Здесь ΔТ – разность температуры нити и трубки, d₁, d₂ – диаметры трубки и проволоки, ℓ – длина нити.

Таким образом, выражение для коэффициента теплопроводности примет вид:

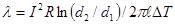. (4)

Если принять температуру трубки равной температуре окружающей среды, то главной трудностью реализации метода будет определение температуры нити, так как ток I через нить и её сопротивление R легко измерить. Преодолеть эту трудность можно, если учесть температурную зависимость сопротивления металла R=Rº(1+αT), где α=2·10^-4K^-1. Если провести измерения сопротивления нити R₀, при температуре окружающей среды Т₀ и сопротивления нити R₁, нагретой до температуры Т₁, то температура проволоки определяется выражением вида: 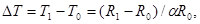где принято, что αT<<1. Подставляя в выражение (1) значение Т₁–Т₂ и значения постоянных получим:

λ=bI²R₁R₀/(R₁-R₀), (5)

где b = 4.83*10^-3. Функционально установка выполнена в виде блочной схемы, представляющей собой монтажную плату стенда, которому подсоединены приборы. Измерение сопротивления нити производится следующим образом: при установки заданного значения тока, ручки магазина сопротивлений должны быть установлены так, чтобы сопротивление магазина было около 700 Ом (сопротивление магазина равно сумме цифр, умноженных на соответствующий множитель). Спустя некоторое время необходимо для установления процесса теплопередачи, переключением ручек малых сопротивлений (≤ 10) добиться установления стрелки нуль–гальванометра на нуль. Тогда показания магазина сопротивлений, делённые на сто, и будут сопротивлением нити. Следует отметить, что влияние лучеиспускания и конвекции на результат измерений пренебрежительно мало вследствие малого объёма трубки, малости поверхности нити и её температуры.

III. Проведение эксперимента и обработка результатов

1. Поставить переключатель основного блока в положение «точно».

1. Включить блок питания в сеть и в положении его переключателя „I“ реостатом установить минимум тока (<0,05A). Выждать 3-5 минут.
2. Произвести измерения сопротивления нити R_o по указанной выше методике. Результат занести в таблицу.
3. Произвести измерения сопротивления нити по п.п. 1- 3, устанавливая соответствующее положение переключателя питания и реостата для значений тока от 0,2 А до 1,0 А. Результаты занести в таблицу.
4. По формуле (5) вычислить значения коэффициента теплопроводности и определить ошибку измерений.
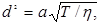
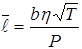
5. Используя связь коэффициента теплопроводности λ с коэффициентом внутреннего трения χ, определить микропараметры движения молекул по формулам: 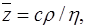где а = 9,83*10^-26, b = 31,8, с = 0,85.
6. Вычислить по формуле (3) значение коэффициента теплопроводности и сравнить с измеренным.
7. Построить график зависимости обратного сопротивления 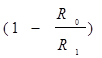от I² графически в соответствии с формулой (5) определить λ: 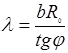, где 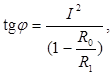φ - угол наклона прямой: .

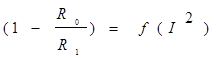Таблица.

№ п/п	I, А	R1	λ		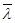δλ	η	d		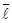	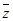λтеор.
1	<0,05
2	0,2
3	0,3
4	0,5
5	0,8
6	1,0

Контрольные вопросы

1. Чем обусловлено возникновение явления переноса в газе и каков их механизм?
2. Как описать процесс теплопроводности с помощью уравнения Фурье?
3. Как объяснить с микроскопической точки зрения явление теплопроводности?
4. Каким образом связан коэффициент теплопроводности с коэффициентом внутреннего трения и микропараметрами газа?
5. Какие, кроме теплопроводности, существуют механизмы теплопередачи и каков их механизм?
6. В чём заключается метод нагретой нити для определения теплопроводности?
7. Как определить температуру нагретой нити?
8. Какова методика измерений сопротивления нити?
9. Почему при выполнении измерений не учитываются другие механизмы теплопередачи?
10. В чём заключается методика измерений коэффициента теплопроводности?
11. Как оценить достоверность результата измерений коэффициента теплопроводности?