Порядок расчета. Обработку результатов двух серий измерений целесообразно осуществлять по алгоритмам [1, с

Обработку результатов двух серий измерений целесообразно осуществлять по алгоритмам [1, с. 122-129] (последовательность расчетов и их содержание определяются условием 10...15 < n < 40...50).

1. Обработать экспериментальные данные в каждой j-й серии отдельно по алгоритму, изложенному в задании 2 (алгоритм обработки многократных измерений), при этом:

– определить оценки результата измерения Q_j и среднего квадратического отклонения s_qj;

– обнаружить и исключить ошибки;

– проверить гипотезу о нормальности распределения оставшихся ре­зультатов измерений.

2. Проверить значимость различия средних арифметических се­рий по алгоритму, представленному на рисунке 48 [1]. Для этого следует:

– вычислить моменты закона распределения разности:

G = ₁ - ₂,

;

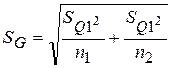– задавшись доверительной вероятностью Р, определить из соответс­твующих таблиц интегральной функции нормированного нормального распределения Ф(t) (таблица 1.1.2.6.2 [2] или таблица Б.1) значение t;

– сравнить |G| с t × S_g.

Если |G| 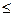t · S_g, то различие между средними арифметическими в сериях с доверительной вероятностью Р можно признать незначимым.

3. Проверить равнорассеянность результатов измерений в сери­ях по алгоритму, изложенному на рисунке 50 [1]. Для этого необходимо:

– определить значение ;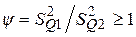

– задавшись доверительной вероятностью Р, определить из соответ­ствующих таблиц (таблица 16 [1] или таблица Е.1) значение аргумента ин­тегральной функции распределения вероятности Фишера y₀;

– сравнить y с y₀.

Если y < y₀, то серии с доверительной вероятностью Р счи­тают рассеянными.

4. Обработать совместно результаты измерения обеих серий с учетом того, однородны серии или нет.

Если серии однородны (равнорассеянны с незначимым различием средних арифметических), то все результаты измерения следует объ­единить в единый массив и выполнить обработку по алгоритму на рисунке 40 [1]. Для этого необходимо:

– определить оценку результата измерения 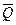и среднего квадратического отклонения S:

;

;

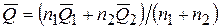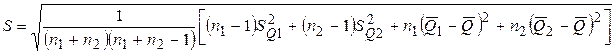– задавшись доверительной вероятностью Р, определить из таблиц распределения Стьюдента (таблица 1.1.2.8 [2] или таблица Д.1) значение t для числа степеней свободы ;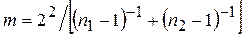

– определить доверительный интервал Е = t×S.

Если серии не равнорассеянны с незначимым различием средних арифметических, то совместную обработку результатов измерений следует выполнять с учетом весовых коэффициентов по алгоритму, представленному на рисунке 51 [1].

Для этого необходимо:

– определить оценки результата измерения – и среднего квадратического отклонения S:

;

;

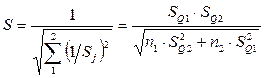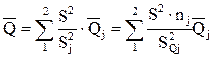– аналогично предыдущему случаю, задавшись доверительной вероят­ностью Р, определить t и доверительный интервал.

Если различие средних арифметических в сериях признано зна­чимым, то результаты измерений в каждой серии следует обработать раздельно по алгоритму многократных измерений:

– в зависимости от закона распределения вероятности результата измерения в каждой серии определить S_j;

– задавшись доверительной вероятностью Р, определить по соответ­ствующим таблицам значение t_j;

– рассчитать доверительный интервал Е_j =S_j × t_j.