БИЛЕТ №18

Волновое уравнение для электромагнитной волны. Рассмотрим нейтральную непроводящую среду с проницаемостями e и m, где и (54) . Поскольку в данном случае плотности токов и зарядов равны нулю (r=0, j=0), уравнения Максвелла в дифференциальной форме будут иметь вид

(I) (II)

(III) (IV).

Подставим в уравнение (III) и продифференцируем его по времени:

,

где мы использовали правило преобразования двойного векторного произведения («bac-cab»):

.

Из (IV) уравнения Максвелла и равенства (54) следует, что , и в результате остается волновое уравнение для вектора (и для вектора , если по тому же рецепту продифференцировать уравнение (I) и т. д…)

, (55)

. (56)

Множитель при второй производной по времени определяет скорость распространения волны

, (57)

что для вакуума (e=1, 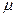=1) дает удивительный результат: скорость волны равна скорости света

. (58)

Таким образом, из уравнений Максвелла следует, что свет является электромагнитной волной. И наоборот, переменное электромагнитное поле в вакууме распространяется со скоростью света, независимо от своей частоты! Рассмотрим простейшую электромагнитную волну.

Плоская электромагнитная волна. Пусть плоская волна распространяется вдоль оси х. Поскольку волновые поверхности (плоскости) будут в этом случае перпендикулярны оси х, то векторы и , а Þ и их проекции на оси y и z не будут зависеть от y и z (иначе волна не могла бы распространяться строго в направлении оси х). Следовательно, в уравнениях Максвелла (I-IV) производные по y и z будут равны нулю и уравнения упрощаются. Чтобы это показать, распишем уравнения Максвелла (rot - с помощью определителей), оставив во всех уравнениях только векторы и , что легко сделать с учетом (54).

(I)

(III)

(IV)

(II)

Распишем векторные уравнения (I) и (III) в проекциях, и то, что осталось от уравнений (IV) и (II) (должно быть всего 8 скалярных уравнений):

, Þ ; (I)

Хочется в этом месте Вас подбодрить, но ничего утешительного сказать не могу,- идём дальше! Будьте внимательны! По разные стороны от знака (=) проекции на разные оси!

, Þ ; (III)

Ничего, что в верхних уравнениях (ох:...) в рамках опущены не равные нулю множители?

(IV) (II).

Из проекций на ох в (I) и (III) следует, что Н_х и Е_х не зависят от времени, а из (IV) и (II) - что эти проекции не зависят также и от х. Следовательно, Н_х и Е_х могут быть только постоянными однородными полями, накладывающимися на поле волны. Они не будут распространяться и поэтому не будут нас в дальнейшем интересовать. Во всяком случае, переменные Н_х и Е_х равны нулю. Следовательно, отличными от нуля переменными компонентами векторов и остаются только их проекции на оси y и z, которые перпендикулярны направлению распространения, следовательно, электромагнитная волна является поперечной. Кроме, того, векторы и ортогональны между собой. Действительно, выпишем рядом третье уравнение из рамки (I) и второе из (III):

; (59)

Из рассмотрения этой пары видно, что изменение во времени поля вдоль оси z порождает электрическое поле вдоль оси y и наоборот: изменение электрического поля вдоль оси y порождает магнитное поле вдоль оси z. При этом не возникает ни поле E_z, ни поле H_y. А это и значит, что ^ . Векторы и в электромагнитной волне взаимно ортогональны! Из полученной пары (59) нетрудно получить волновое уравнение, например, продифференцировать первое из них по координате, а второе по времени. После чего будет легко увидеть, что вторые производные от E_y по времени и координате связаны волновым уравнением

, (60)

и аналогично можно получить волновое уравнение для H_z

. (61)

Ранее из уравнений Максвелла были получены волновые уравнения (55,56) в более общем случае, что позволяет уравнения (60,61) написать для любой проекции. Но тогда мы потеряли бы информацию о геометрии волны.

Как связаны мгновенные значения и ? Пусть E_y = E_y (t-x/с), H_z= H_z (t-x/с). Обозначим фазу φ≡(t-x/с) и вычислим производные: от E_y по координате х; от H_z по времени:

; .

Подставим эти производные в первое из уравнений (59)

,Þ

, где константа обусловлена наличием постоянной компоненты полей. Нас интересует только переменное поле, для которого положим const=0, Þ

. (62)

Это означает, что векторы и изменяются синхфазно, в частности, одновременно обращаются в нуль и достигают максимумов/минимумов. Кроме того, эти векторы составляют правовинтовую систему с направлением распространения (рис.14). По этим свойствам и направлению распространения волны можно однозначно определить в каких именно плоскостях колеблются векторы и ( - в плоскости xy; - в плоскости xz) , поэтому уравнения плоской электромагнитной волны принято записывать без указания проекций:

Е=E_m cos(wt-kx); H=H_m cos(wt-kx). (63)

NB!Обратите внимание! На рис.14 изображена электромагнитная волна: векторы и в каждой точке оси х в некоторый момент времени! Через время, равное половине периода колебаний картина изменится (рис.15). Вообще картина непрерывно изменяется не только в пространстве, но и во времени!

Полезный совет: обратите внимание сейчас, что изображенные на рис. 14 и 15 мгновенные фотографии волны позволяют наглядно увидеть, что вектор в процессе распространения волны все время колеблется в плоскости xy! Поэтому данная волна является плоско-поляризованной! Обязательно вернитесь к этим картинкам позже, когда мы будем изучать поляризованный свет.