Вопрос 23.2. бином ньютона

Рассмотрим степенную функцию 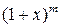, где m ‑ натуральное число. Разложим ее в окрестности 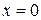по формуле Маклорена m-го порядка. Тогда получим

.

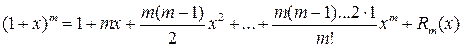Согласно формуле Лагранжа остаточный член 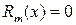. Коэффициенты разложения называются биноминальными коэффициентами и обозначаются

, , ,…,

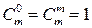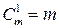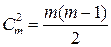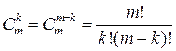
Тогда получим

.

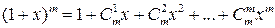Теперь несложно получить общую формулу бинома Ньютона

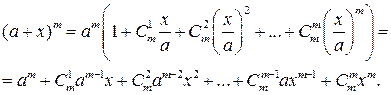
Пример 23.5.

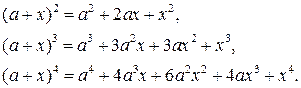
Конец примера.

Биноминальные коэффициенты обладают следующими свойствами:

, , , .

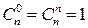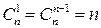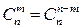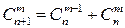Биномиальные коэффициенты можно легко определить из треугольника Паскаля, который строится на основе последней формулы

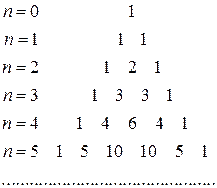
Например, коэффициенты 4-й строки получаются так:

.

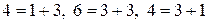ЛЕКЦИЯ № 24. ЭКСТРЕМУМЫ И ТОЧКИ ПЕРЕГИБА ФУНКЦИИ.

Вопрос 24. 1. Необходимые и достаточные условия существования локального экстремума функции.

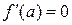Теорема 24.1.(Необходимое условие существования локального экстремума функции). Пусть функция точке a имеет локальный экстремум. Тогда или , или 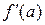не существует.

Доказательство. Если 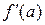существует, то в силу теоремы Ферма 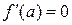(в точке локального экстремума производная дифференцируемой функции равна нулю). Остается еще одна возможность, что 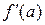не существует.

Конец доказательства.

Пример 24.1. 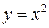, 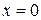‑ точка локального минимума, 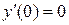. 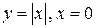‑ точка локального минимума, 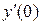не существует.

Конец примера.

Определение 24.1. Те точки функции , в которых 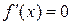, называются стационарными.

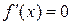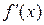Определение 24.2. Те точки функции , в которых или не существует, называются критическими точками первого рода.

Из теоремы 24.1 следует, что точки локального экстремума нужно искать среди критических точек 1-го рода, однако не всякая критическая точка 1-го рода является точкой локального экстремума, например у функции 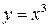, , 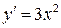стационарная точка 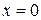не является точкой локального экстремума.

Теорема 24.2. (Достаточные условия существования локального экстремума функции). Пусть непрерывна в некоторой окрестности точки a, и дифференцируема в этой окрестности, за исключением может быть самой точки a. Тогда

1) если при переходе через точку a знак 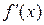не изменяется, то в точке a экстремума нет.

2) если при переходе через точку a знак производной 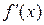изменяется на противоположный, то a ‑ точка локального экстремума, причем, если знак меняется с «‑» на «+», то a ‑ точка локального максимума, если знак меняется с «+» на «‑» , то a ‑ точка локального минимума.

Доказательство. 1) Докажем первую часть теоремы. Пусть для определенности знак производной положителен 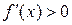и не меняется при переходе через точку a. Тогда, применяя теорему Лагранжа, получим

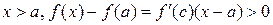, т.е. ,

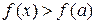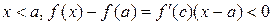, т.е. ,

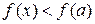и, следовательно, a не является точкой локального экстремума. Пусть теперь знак производной отрицателелен 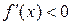и не меняется при переходе через точку a. Тогда, опять применяя теорему Лагранжа, получим

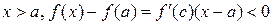, т.е. ,

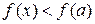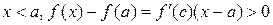, т.е. ,

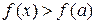откуда следует, что a не является точкой локального экстремума и в этом случае.

Докажем вторую часть теоремы. Пусть для определенности знак производной меняется с «‑» на «+» при переходе через точку a. Тогда, применяя теорему Лагранжа, получим

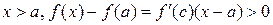, т.е. ,

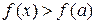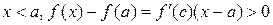, т.е. ,

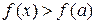и, следовательно, a есть точка локального минимума. Аналогично доказывается наличие локального максимума при изменении знака производной с «+» на «‑».

Конец доказательства.

Из этой теоремы вытекает правило знаков:

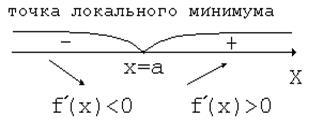
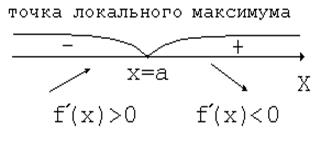
Пример 24.2.

1) 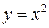, , 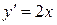, 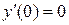тогда 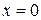критическая точка функции.

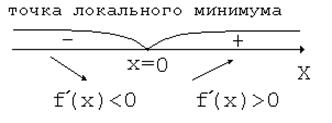
2) 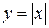, 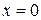критическая точка функции, поскольку производной 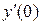не существует

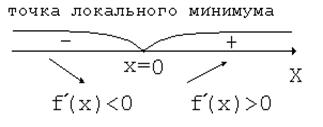
Конец примера.

Теорема 24.3. (Второе достаточное условие существования локального экстремума функции). Пусть в точке a функция n раз дифференцируема и производные функции в плоть до 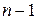‑го порядка равны нулю

,

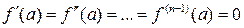а производная n‑го порядка отлична от нуля 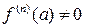. Тогда, если n – нечетное натуральное число, то в точке a экстремума нет. Если n ‑ четное натуральное число, то экстремум есть, причем, если

a) 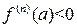, то в точке a локальный максимум.

б) 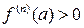, то в точке a локальный минимум.

Доказательство. Разложим в окрестности точки a по формуле Тейлора с остаточным членом в форме Пеано:

.

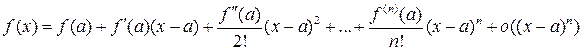Так как все производные до 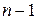порядка включительно равны 0, то

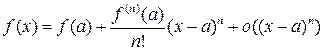
или

.

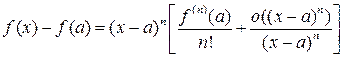Если x близко к a, то знак выражения в квадратных скобках определяется n-й производной, поэтому, если n нечетно, то разность 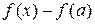меняет свой знак одновременно с разностью 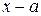, поэтому в точке a экстремума нет. Если n четно, то знак разности 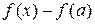совпадает со знаком n-й производной и не завист от знака разности 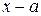. Следовательно, при отрицательной производной 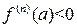получаем локальный максимум, при положительной производной 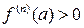‑ локальный минимум.

Конец доказательства.

Пример 24.3. 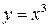, в точке 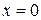имеем 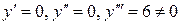, следовательно, x=0 не является точкой экстремума, так как первая отличная от нуля производная третьего , то есть нечетного, порядка.

Конец примера.