Приведение рядов динамики к одному основанию
| Показатели | Кварталы | ||
| I | II | III | |
| 1. Среднемесячная выработка рабочего, шт. | |||
| 2. Среднемесячная заработная плата рабочего, ден.ед. | |||
| 3. Темп роста среднемесячной выработки (выработка I квартала = 100%), % | 100,0 | 102,7 | 105,4 |
| 4. Темп роста среднемесячной заработной платы (зарплата I квартала = 100%), % | 100,0 | 101,7 | 103,4 |
Из данных таблицы 7.5 видно, что среднемесячная выработка и заработная плата рабочего увеличиваются, однако разная размерность и разный исходный уровень этих показателей не позволяют определить, уровень какого из них изменяется более быстрыми темпами. В этой связи оба динамических ряда приводят к одному основанию, приняв в качестве базы сравнения начальный уровень ряда. Из расчетов (стр.3 и 4) видно, что среднемесячная выработка увеличивается более быстрым темпом, чем среднемесячная заработная плата.
Задача 5
Пример расчета уравнения линейного тренда для выявления тенденции изменения следующих показателей:
Таблица 7.6
Аналитическое выравнивание по прямой линии
| Периоды времени - i | Значение показателя -Yi | t | t2 | Yi*t | Yt |
| -3 -2 -1 | -300 -220 -120 | ||||
| Итого | åt=0 |
Рассчитаем параметры уравнения тренда:
; 
.
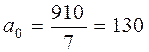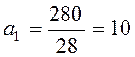Таким образом, уравнение тренда будет иметь вид:
Yt = 130+10t.
Величина стандартизированной ошибки аппроксимации (se) равна нулю. Следовательно, построенное уравнение тренда хорошо отражает тенденцию развития.
Задача 6
По данным о товарообороте группы предприятий массового питания (табл. 7.7, столбцы 1-4) необходимо определить индексы сезонности товарооборота.
Таблица 7.7
Средний товарооборот, тыс.ден.ед.
| Месяц | Уровни, тыс.ден.ед. (Yi) | В среднем за три года ( 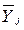 ) | Индекс сезонности (isj) | ||
| 1-й год | 2-й год | 3-й год | |||
| Январь | 74,3 | 73,2 | 77,2 | 74,9 | 89,3 |
| Февраль | 78,4 | 82,8 | 75,1 | 78,8 | 93,9 |
| Март | 79,3 | 83,4 | 76,5 | 79,7 | 95,0 |
| Апрель | 80,9 | 83,5 | 84,4 | 82,9 | 98,8 |
| Май | 81,1 | 85,4 | 83,6 | 83,4 | 99,4 |
| Июнь | 102,9 | 108,4 | 110,0 | 107,1 | 127,7 |
| Июль | 101,0 | 92,4 | 100,8 | 98,1 | 116,9 |
| Август | 83,3 | 84,0 | 87,6 | 84,8 | 101,1 |
Продолжение таблицы 7.7
| Месяц | Уровни, тыс.ден.ед. (Yi) | В среднем за три года ( 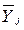) | Индекс сезонности (isj) | ||
| 1-й год | 2-й год | 3-й год | |||
| Сентябрь | 85,7 | 85,9 | 78,9 | 83,5 | 99,5 |
| Октябрь | 81,3 | 75,0 | 82,6 | 80,6 | 96,1 |
| Ноябрь | 76,7 | 78,2 | 80,4 | 78,4 | 93,5 |
| Декабрь | 73,1 | 73,8 | 76,8 | 74,4 | 88,7 |
В среднем за год ( 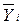 ) | 83,4 | 83,8 | 84,4 | 83,9 | 100,0 |
Решение.
Вначале определим средние уровни одноименных внутригодовых периодов:
- для января: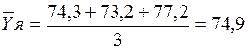 
тыс.ден.ед.;
- для февраля: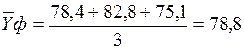 
тыс.ден.ед.;
- для марта: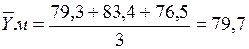 
тыс.ден.ед. и т. д.
Для остальных месяцев средние уровни определяются аналогично, значения занесены в гр.5 табл. 7.7.
В итоговой строке гр.5 определена общая средняя:
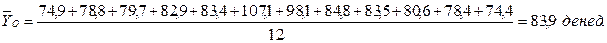Этот общий средний уровень используется в качестве постоянной базы сравнения при определении средних индексов сезонности (гр.6, табл.7.7):
для января: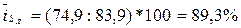 
для февраля: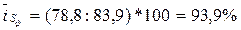 
;
для марта: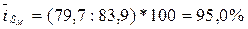 
и т.д.
Для остальных месяцев средние индексы сезонности определяются аналогично, значения занесены в гр.6 табл. 7.7. Из гр.6 видно, что сезонные колебания товарооборота группы предприятий характеризуются повышением в июне (+27,7%) и июле (+16,9%), а также понижением в декабре (-11,3%).
Задача 7
При административно-территориальных изменениях, например, при объединении предприятия (изменении границ) получены следующие данные по объему производства:
Таблица 7.8