Раздел 12 Теория дифференциальных уравнений

ГЧ, ГИ 2 курс

ТРЕТИЙ СЕМЕСТР

Раздел 10 Элементы теории функций нескольких переменных

Тема 10.1 Функция двух и более переменных 2/2

Функция нескольких переменных. Область существования. Способы задания функций. Предел функции нескольких переменных. Непрерывность функции нескольких переменных.

Тема 10.2 Частные производные и полный дифференциал функции двух и более переменных 2/2

Частные приращения и полное приращение функции двух и более переменных. Частные производные функции нескольких переменных. Частные производные сложной функции двух переменных, полная производная. Применение полного дифференциала к приближенным вычислениям.

Тема 10.3 Частные производные и полные дифференциалы высших порядков 2/2

Частные производные и дифференциалы высших порядков для функции многих переменных. Дифференцирование функций нескольких переменных, заданных неявно. Формула Тейлора для функции двух переменных.

Тема 10.4 Экстремум функции двух переменных 2/2

Экстремумы функции двух переменных, необходимое и достаточные условия существования экстремумов.

Тема 10.5 Касательная плоскость и нормаль к поверхности, производная по направлению, градиент 2/2

Уравнение касательной к пространственной линии. Касательная плоскость и нормаль к поверхности. Производная по направлению. Градиент и его свойства. Теорема о связи градиента и производной по направлению.

Тема 10.6 Метод наименьших квадратов 2/2

Раздел 11 Кратные интегралы

Тема 11.1 Общая схема построения кратных интегралов 2/2

Понятие определенного интеграла по фигуре: плоской области, линии в пространстве, пространственного тела, поверхности. Общая схема построения интегральных сумм и названия кратных интегралов. Основные свойства кратных интегралов.

Тема 11.2 Двойной интеграл 2/2

Двойной интеграл, его вычисление, свойства. Замена переменных в двойном интеграле. Двойные интегралы в полярных координатах. Применение двойных интегралов для вычисления площадей, объемов, моментов инерции, координат центра тяжести плоских фигур.

Тема 11.3 Тройной интеграл, его вычисление 2/2

Тройные интегралы, определение и свойства. Трехкратные интегралы в цилиндрической и сферической системах координат. Якобиан преобразования. Применение тройных интегралов.

Тема 11.4 Криволинейные интегралы 2/2

Криволинейные интегралы первого и второго рода, их свойства и вычисление. Применение криволинейных интегралов первого и второго рода для решения геометрических задач и задач механики. Условия независимости интеграла от пути интегрирования. Формула Грина.

Тема 11.5 Поверхностные интегралы 2/2

Поверхностные интегралы, их свойства и вычисление. Односторонние и двусторонние поверхности. Формула Стокса. Формула Остроградского. Оператор Гамильтона.

Раздел 12 Теория дифференциальных уравнений

Тема 12.1 Дифференциальные уравнения первого порядка 4/4

Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка, основные понятия. Задача Коши. Теорема существования и единственности решения. Дифференциальные уравнения первого порядка с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка. Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли.

Тема 12.2 Дифференциальные уравнения высших порядков 2/2

Дифференциальные уравнения высших порядков, основные понятия. Задача Коши и ее решение. Основные типы уравнений допускающие понижение порядка.

Тема 12.3 Линейные дифференциальные уравнения высших порядков 2/2

Линейные дифференциальные уравнения высших порядков с произвольными коэффициентами. Линейный оператор, его свойства, основные теоремы. Понятие определителя Вронского. Фундаментальная система решений. Теорема о структуре общего решения линейного дифференциального уравнения.

Тема 12.4 Однородные линейные дифференциальные уравнения 2/2

Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Три случая частных решений.

Тема 12.5 Неоднородные линейные дифференциальные уравнения со специальной правой частью 1/2

Решение неоднородных линейных дифференциальных уравнений высших порядков со специальной правой частью. Определение частного решения по виду правой части.

Тема 12.6 Элементы теории уравнений математической физики 2/2

Основные типы уравнений математической физики: волновое уравнение, уравнение теплопроводности, уравнение Лапласа. Вывод уравнения колебания струны. Формулировка краевой задачи.

Раздел 13

Тема 13.1 Числовые ряды.Частичные суммы числовой последовательности. Сумма последовательности и ее суммируемость. Понятие числового ряда и примыкающие понятия. Сходящийся (расходящийся) ряд. Линейные операции над сходящимися рядами. Необходимое условие сходимости числового ряда. Гармонический ряд. Абсолютно сходящийся ряд. Критерий сходимости неотрицательного ряда. Признаки сравнения неотрицательных рядов. Интегральный признак сходимости. Признаки Коши и Даламбера сходимости числовых рядов и их сравнение. Знакочередующиеся ряды. Признак Лейбница. Перестановка членов абсолютно сходящегося ряда. Условно сходящиеся ряды. Перестановки членов условно сходящегося ряда

Тема 13.2 Функциональные последовательности и функциональные ряды. Область сходимости и поточечный предел функциональной последовательности. Сходимость поточечная и равномерная. Функциональный ряд и примыкающие понятия. Равномерно сходящийся функциональный ряд. Критерий равномерно сходящегося функционального ряда.

Признак равномерной и абсолютной сходимости Вейерштрасса. Непрерывность поточечного предела (поточечной суммы) равномерно сходящейся последовательности (равномерно сходящегося функционального ряда). Почленное интегрирование и дифференцирование функциональных рядов.

Тема 13.3 Степенные ряды. Понятие степенного ряда. Основная теорема о степенных рядах. Лемма Абеля. Интервал и радиус сходимости. О равномерной сходимости степенного ряда. О непрерывности поточечной суммы степенного ряда. Почленное интегрирование и дифференцирование степенных рядов.

Понятие ряда Тейлора с заданным центром. О разложении функции в ряд Тейлора. Связь с остаточным членом формулы Тейлора. Разложение функций 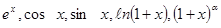в степенные ряды. Приближенное вычисление значений функций и интегралов с помощью степенных рядов.

Последовательности и ряды с комплексными членами.

ПБ 2 курс

ТРЕТИЙ СЕМЕСТР