Спряжені, самоспряжені диференціальні оператори, крайові умови і крайові задачі

Спряженим з диференціальним оператором

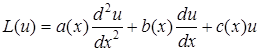(5.93)

називають диференціальний оператор наступного вигляду

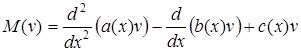. (5.94)

Властивість спряженості двох операторів є взаємною, тобто спряженим до диференціального оператора 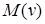буде диференціальний оператор .

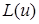Якщо 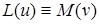, то оператор 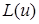називають самоспряженим.

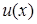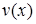Характерна властивість спряжених диференціальних операторів: для будь-яких двічі неперервно диференційованих функцій і виконується співвідношення

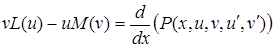. (5.95)

Дійсно

.

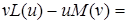
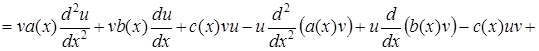
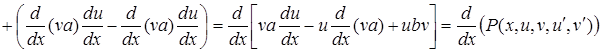Нехай 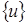і 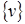– дві множини функцій, які задовольняють деяким однорідним крайовим умовам А і В відповідно на [a,b]. Тоді, якщо для довільних функцій з цих множин виконується співвідношення

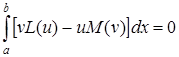, (5.96)

то крайові умови А та В називають спряженими крайовими умовами, які відповідають диференціальним операторам 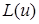і .

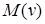Крайову задачу для диференціального рівняння 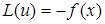при крайових умовах А і крайову задачу 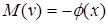при крайових умовах В ( 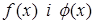– задані функції) називають спряженими крайовими задачами.

Якщо при цьому диференціальний оператор 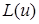самоспряжений і крайові умови А ''самоспряжені'', тобто співпадають з крайовими умовами В, то крайова задача для 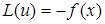при крайових умовах А називається самоспряженою крайовою задачею.

5.5.4.Зведення лінійного однорідного диференціального рівняння другого порядку до самоспряженого вигляду

Означення 5.6. Лінійне однорідне диференціальне рівняння в якому коефіцієнт при 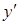дорівнює похідній від коефіцієнта при 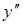, тобто диференціальне рівняння (5.81) має вигляд

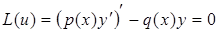(5.97)

називають самоспряженим диференціальним рівнянням другого порядку.

Твердження 5.1. Довільне лінійне однорідне диференціальне рівняння другого порядку

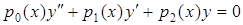, (5.98)

коефіцієнти якого неперервні н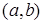а , а 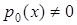і є неперервно диференційованою функцією на 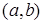, завжди можна привести до самоспряженого вигляду домноженням на деяку функцію від х.

Доведення. Домножимо (5.89) та :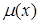

.

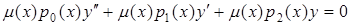Виберемо 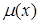згідно умовам 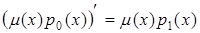. Звідки 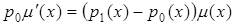, тобто

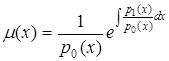. (5.99)

Домножаючи диференціальне рівняння (5.98) на функцію (5.99), отримаємо

.

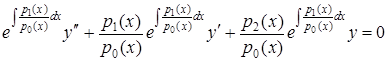Позначивши 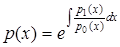, перепишемо диференціальне рівняння так

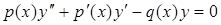, де .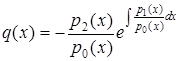

Твердження доведено.

5.5.5. Задача Штурма-Ліувілля

Це задача про власні значення і власні функції: на відрізку 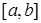знайти двічі неперервно диференційовані не рівні тотожно нулю розв'язки крайової задачі

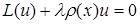
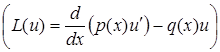, (5.100)

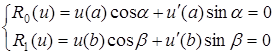(5.101)

і визначити відповідні їм значення параметра 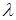. Тут 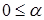, 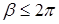– постійні числа, 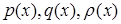– неперервні на 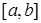функції, причому , .

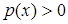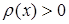Вказані розв'язки називають власними або фундаментальними функціями, а відповідні їм числові значення 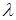називають власними значеннями або власними числами.

Властивості оператора :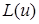

а) справедливе співвідношення

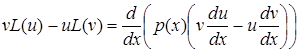. (5.102)

Дійсно

.

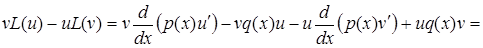
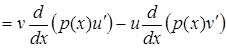З іншого боку

.

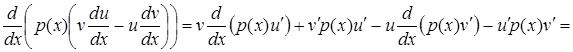
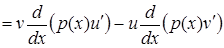Твердження доведено;

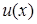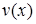б) якщо і задовольняють умові (5.101), то

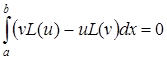. (5.103)

Дійсно

.

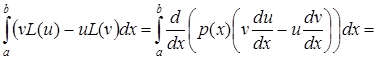
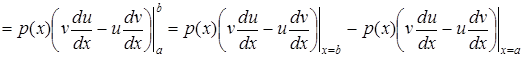Згідно крайових умов

,

,

,

.

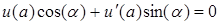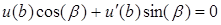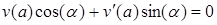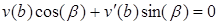Розглянемо дві системи: перше і третє, друге і четверте рівняння. Для першої системи 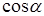і 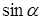розглядаємо як ненульовий розв'язок 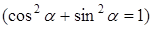. Це можливо тоді і тільки тоді, коли

.

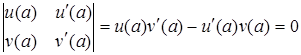Аналогічно можна отримати 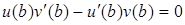. Співвідношення (5.103), таким чином, буде виконуватися.

Властивості власних значень і власних функцій задачі Штурма-Ліувілля:

а) власні функці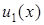ї і 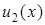, що відповідають різним власним значенням 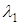і 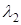, ортогональні з ваговою функцією 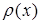, тобто

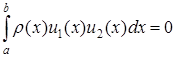. (5.104)

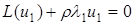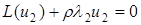Дійсно, домножаючи рівняння і відповідно на 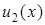і 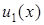і проінтегрувавши їх різницю, отримаємо

.

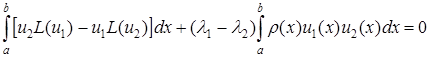Згідно властивості б) перший доданок дорівнює нулю, так як 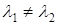, то виконується (5.104);

б) всі власні значення дійсні.

Дійсно, якби знайшлося комплексне власне значення 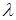з власною функцією 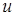, то спряжене з ним комплексне число 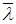також було б власним значенням, а функція 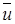була б його власною функцією. З ортогональності власних функцій 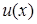та 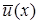випливає

,

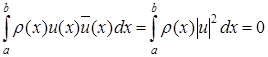тобто 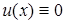. Це означає, що число 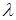не є власним значенням;

в) будь-якому власному значенню відповідає тільки одна лінійно незалежна власна функція.

Дійсно, припустимо, що маємо дві лінійно незалежні власні функці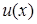ї і 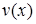, які відповідають одному власному значенню 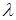. Тоді ліва частина в (5.102) дорівнює нулю, так як 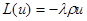, 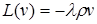. Тому

,

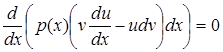тобто

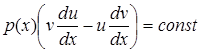. (5.105)

Ліва частина співвідношення (5.105) в точці 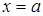дорівнює нулю, так як для функцій 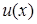і 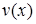виконується крайові умови. Постільки 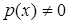, то в точці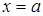 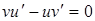. Це означає, що в точці 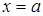вронскіан від функцій 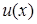і 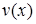дорівнює нулю. Тобто функці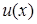ї і 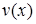– лінійно-залежні;

г) довільну власну функцію 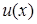можна пронормувати

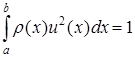. (5.106)

5.5.6. Функція Гріна

Припустимо, що 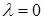не є власним значенням задачі Штурма-Ліувілля (5.100), (5.101). Тоді крайова задача не має ненульових розв'язків. Нехай функцій 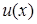і 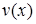– розв'язки рівняння 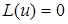, які задовольняють відповідно крайові умови 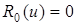та .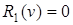

Такі розв¢язки існують і їх можна отримати як розв¢язки задачі Коші, наприклад, при початкових умовах:

, ; , .

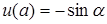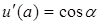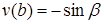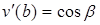Функці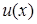ї і 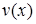будуть лінійно–незалежні, інакше якби 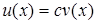, де с– постійна, то виконувалися б умови 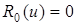, 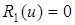. А це б означало, що задача (5.100),(5.101) при 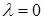мала б ненульовий розв'язок. В силу (5.102)

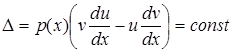(5.107)

і ця константа, в силу лінійної незалежності функцій 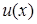і 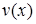, буде відмінною від нуля.

Функцію

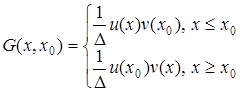(5.108)

будемо називати функцією впливу або функцією Гріна крайової задачі (5.100), (5.101) при 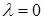, тобто

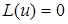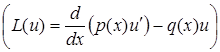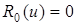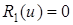, , , . (5.109)

Властивості функції Гріна:

а) функція Гріна неперервна на ;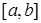

б) на кожному з інтервалів 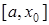, 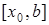двічі неперервно диференційовна і задовольняє рівняння ;

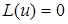в) , ;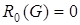

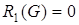г) ;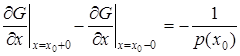

д) функція Гріна є симетричною функцією, тобто .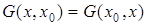

Властивості а), б), в), д) випливають з побудови функції Гріна у вигляді (5.108).

Доведемо властивість г):

; .

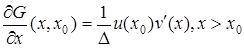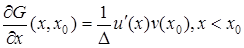Тому

.

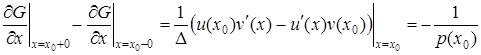Приведемо без доведення ряд теорем, які часто використовуються при розв'язанні різних прикладних задач.

Теорема 5.5. (Про інтегральне представлення розв'язку з допомогою функції Гріна). Якщо 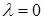не є власним числом задачі Штурма-Ліувілля (5.100), (5.101), тобто якщо крайова задача (5.109) має ненульовий розв'язок, то для того , щоб функція 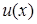була двічі неперервно диференційовним на 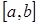розв'язком крайової задачі

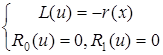(5.110)

необхідно і достатньо, щоб

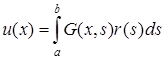, (5.111)

де 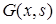-функція Гріна крайової задачі (5.109).

Теорема 5.6. Якщо 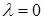не є власним числом задачі Штурма-Ліувілля (5.100), (5.101), то для того, щоб функція 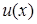була двічі неперервно диференційовним розв'язком цієї задачі на 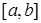необхідно і достатньо, щоб вона була розв'язком інтегрального рівняння

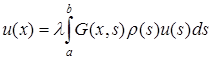, (5.112)

де функція 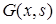– функція Гріна крайової задачі (5.109).

Теорема 5.7 (В.А. Стеклова про розклад функції в ряд). Довільна двічі неперервно диференційовна функція 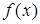на 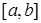, яка задовольняє крайовим умовам 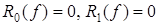, розкладається на цьому відрізку по власним функціям задачі Штурма-Ліувілля (5.100), (5.101) в абсолютно і рівномірно збіжний ряд Фур'є

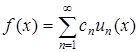, (5.113)

де 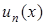– власні функції задачі Штурма-Ліувілля (5.100), (5.101), які відповідають власним значенням 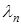і задовольняють умові ортогональності з ваговою функцією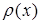

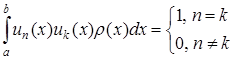, (5.114)

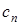коефіцієнти Фур'є функції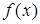

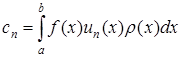. (5.115)