Тема 1, 2. Елементи комбінаторики. Перестановки, сполучення та розміщення. Завдання для самоконтролю:

Завдання для самоконтролю:

2.1. Розв’язати задачу: Скільки чотиризначних чисел, кратних 5, усі цифри яких різні, можна записати, використовуючи лише цифри 1, 2, 3, 4 і 5 ?

2.2. Скільки телефонних номерів можна скласти з п’яти цифр так , щоб в кожному окремо взятому номері всі цифри були різні ?

3.3. У групі 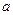дівчат і 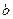хлопців. Скількома способами можна вибрати редколегію класної стіннівки із трьох осіб, щоб серед них обов’язково були і хлопці і дівчата ?

Питання для самоконтролю:

1. Види сполук.

2. Формули для обчислення числа перестановок, розміщень і сполучень.

3. Правила суми і добутку для розв’язування комбінаторних задач.

Тема 3, 4. Розв’язування задач на обчислення ймовірностей подій.

Завдання для самоконтролю:

4.1. Із 1000 надрукованих настінних календарів виявилось 5 бракованих. Навмання взяли один календар. Яка імовірність того, що він бракований ?

4.2. У лотереї випущено 10 000 квитків і встановлено: 10 виграшів по 200 грн., 100 – по 100 грн., 500 – по 25 грн. і 1000 виграшів по 5 грн. Громадянин купив 1 квиток, Яка ймовірність того, що він виграє не менше ніж 25 гр. ?

4.3. У набірному цеху типографії працюють набірники. Імовірність допустити помилку кожного з них відповідно дорівнює 0,01; 0,02; 0,03. Яка ймовірність того, що після закінчення роботи буде допущено одну помилку ?

Питання для самоконтролю:

1. Класичне означення ймовірності.

2. Теорема про ймовірність суми двох несумісних подій.

3. Теорема про ймовірність добутку двох подій.

4. Формула повної ймовірності.

5. Формула Байєса.

Тема 5. Схема Бернуллі.

Завдання для самоконтролю:

5.1. Монету підкидають 10 разів. Яка ймовірність того, що 8 разів вона випаде числом вверх ?

5.2. Баскетболіст проводить 4 кидки по корзині з однієї й тієї ж позиції. Ймовірність попадання при одному кидку дорівнює 0,8. Яка ймовірність того, що він попаде в корзину рівно 3 рази ?

Питання для самоконтролю:

1. Незалежні випробування.

2. Формула Бернуллі.

ЛІТЕРАТУРА:

1. Бугір М.К. Теорія ймовірностей та математична статистика. – Тернопіль: Підручники та посібники, 1998. – 176 с.

2. Васильченко І.П. Вища математика для економістів (спеціальні розділи). – К.: Кондор, 2004. – 348 с.

3. Вища математика: Збірник задач. У двох частинах. Ч.2 / П.П.Овчинников, П.С.Кропив’янський та ін. – К.: Техніка, 2003. – 376 с.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая шк., 1999. – 399 с.

5. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая шк., 1998. – 480 с.

6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.2. – М.: Наука, 2000. – 416 с.

7. Дюженкова Л.І., Дюженкова О.Ю., Михалін Г.О. Вища математика. Приклади і задачі. – К.: ВЦ “Академія”, 2002. – 623 с.

8. Овчинников П.П. Вища математика. Ч.2. – К.: Техніка, 2000. – 792 с.

9. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.2. – М.: Наука, 1985. – 560 с.

10. Соколенко О.І. Вища математика. – К.: Видавничий центр “Академія”, 2002. – 430 с.

11. Пасічник І.В., Сясєв А.В., Маринчук Л.В. Теорія ймовірностей та випадкові процеси. Ч.1: Конспект лекцій. – Дніпропетровськ, НМетАУ. – 2005.

12. Теорія ймовірностей та випадкові процеси. Частина II: Конспект лекцій / Л.В. Маринчук, І.В. Пасічник, А.В. Сясєв, А.Г. Моня. – Дніпропетровськ: НМетАУ, 2006. – 48 с.

13. Шефтель З. Г. Теорія ймовірностей. – К.: Вища шк., 1994, – 192 с.

ВІДПОВІДІ ДО ЗАВДАНЬ САМОКОНТРОЛЮ:

2.1. 24 .

2.2. 30240.

2.3. .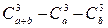

4.1. 0,005.

4.2. 0,061.

4.3. 0,06.

5.1. 0,044.

5.2. 0,4096.

альний посібник. - К.тематической статистике: Учеб. пособие г