Методы анализа сложных линейных

ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Методические указания

При подготовке к занятию следует изучить соответствующий теоретический материал: [1, с.202–207; 210–229; 235–242]; [2, с.224–242; 249–256; 260–264].

Ответьте на следующие вопросы:

1. Как сформировать – матрицу соединений (инциденций)?

2. Введите в– вектор токов ветвей схемы и сформируйте 1-й закон Кирхгофа в матричной форме с помощью матрицы .

3. Дайте правило формирования – матрицы основных сечений.

4. Приведите выражение 1-го закона Кирхгофа в матричной форме с помощью матрицы .

5. Введите вектор в – напряжений ветвей схемы. Определите основной контур графа и дайте правило формирования – матрицы основных контуров.

6. Сформируйте выражение 2-го закона Кирхгофа в матричной форме с помощью матрицы .

7. В обобщенной ветви ЭЦ ее элементы , , могут быть включены двумя способами, как показано ниже на рисунке:

Выведите формулы, позволяющие вычислить через , , , , а также вычислить через , , , , . Убедитесь в том, что для двух приведенных схем эти формулы, так называемые компонентные уравнения, идентичны.

Поясните, как учитываются условные положительные направления источников , в том случае, если они не совпадают с условными направлениями , .

Введите диагональные матрицы параметров ветвей в или в, столбцовые матрицы (векторы) в – токов ветвей, в – напряжений ветвей, – источников напряжений, – источников токов и сформируйте все компонентные уравнения для данной схемы в матричной форме.

З а д а ч а 4

Для каждого из вариантов схем из табл.4.1:

– постройте граф схемы и выделите в нем жирными линиями дерево, которое определено дугами графа, перечисленными в столбце 4;

Таблица 4.1

Исходные данные к задаче 4

Окончание табл.4.1

– сформируйте уравнение по 1-му закону Кирхгофа для узла, заданного в столбце 5;

– сформируйте уравнение по 2-му закону Кирхгофа для основного контура, ассоциированного с хордой (связью), номер которой указан в столбце 6;

– определите число независимых уравнений, которые могут быть составлены по 1-му и 2-му законам Кирхгофа. Сравните эти числа с числом ветвей дерева и числом хорд (связей);

– составьте матрицу инциденций (связей), если базисный узел задан в табл.4.1;

– перечислите множества дуг каждого из основных сечений и составьте матрицу основных сечений;

– перечислите множества дуг каждого из основных контуров и составьте матрицу основных контуров.

ЗАНЯТИЕ 5

МЕТОДЫ АНАЛИЗА СЛОЖНЫХ ЛИНЕЙНЫХ

ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ (продолжение)

Методические указания

При подготовке к занятию следует изучить соответствующий теоретический материал: [1, с.202–207; 210–229; 235–242]; [2, с.224–242; 249–256; 260–264].

Выполните следующие задания и ответьте на вопросы:

1. В схему, содержащую р ветвей и q узлов, введите узловые напряжения. Сколько их должно быть?

Введите векторы в – напряжений ветвей схемы, у – ее узловых напряжений и покажите их связь с помощью – матрицы инциденций.

2. Взяв за основу выражение 1-го закона Кирхгофа в матричной форме в = и применив компонентные уравнения в виде

в = в в + + в ,

получите уравнение для вектора узловых напряжений у:

у у = у,

где у= в ,

у = – – в .

Представьте его в развернутом виде в форме системы узловых уравнений, составляющих основу метода узловых напряжений анализа ЛЭЦ.

3. Взяв за основу выражение 2-го закона Кирхгофа в матричной форме в= и применив компонентные уравнения в виде

в= в в – – в ,

получите уравнение для вектора контурных токов к:

к к = к,

где к= в ,

к= + в .

Представьте его в развернутом виде в форме системы контурных уравнений, составляющих основу метода контурных токов анализа ЛЭЦ.

З а д а ч а 5

По заданному графу (рис.5.1,а) и назначенным схемам отдельных ветвей в соответствии с их кодировкой постройте резистивную схему ЭЦ. Все необходимые сведения для этого представлены в таблицах 5.2, 5.3.

Для построенной схемы:

1) в соответствии с заданным базисным узлом введите узловые напряжения и сформируйте систему узловых уравнений. Решите ее, найдите напряжения и токи всех ветвей;

2) в соответствии с назначенным деревом графа назовите его хорды (связи), покажите на графе и схеме цепи все основные контуры, контурные токи и их условные положительные направления. Сформируйте систему контурных уравнений, решите их и с помощью найденных контурных токов определите токи ветвей. Сравните результаты расчетов обоими методами;

3) по отношению к току первой ветви I₁ примените принцип наложения, вычислив его как сумму токов, создаваемых каждым из заданных источников в отдельности.

В табл.5.1 приведены числовые значения параметров резисторов, а также задающие напряжения и токи источников.

Таблица 5.1

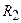Ом

Ом

Ом

Ом

Ом

Ом

В

В

В

В

В

А

А

А

А

А

Таблица 5.2

Кодировка ветвей к задаче 5

Таблица 5.3

Типы ветвей к задаче 5

Вариант	Номера ветвей Коды ветвей из табл.5.2	Базисный узел	Ветви дерева	Вариант	Номера ветвей Коды ветвей из табл.5.2	Базисный узел	Ветви дерева
								4 5 6									1 2 4
								3 4 6									2 5 6
								3 4 5									2 3 6
								2 5 6									2 3 5
								2 4 6									1 5 6
								2 3 6									1 3 6
								2 3 5									1 3 5
								2 3 4									1 3 4
								1 5 6									1 4 5
								1 4 5									1 2 6
								1 3 6									1 2 5
								1 3 5									2 3 4
								1 3 4									1 3 4
								1 2 6									1 2 6
								1 2 5									2 4 6

На рис.5.1,б для примера построена схема со следующим набором кодов ветвей:

Номер ветви
Ее код

Рис. 5.1. Граф цепи и схема к задаче 5:

а) – граф цепи; б) – схема одного из вариантов

ЗАНЯТИЕ 6