Уравнение диффузии

Уравнения переноса

Общая форма:

Здесь ρ - плотность чего-либо, D - коэффициент диффузии, V - скорость переноса ("конвективного").

Примеры:

Уравнение Нернста-Планка (закон сохранения массы, числа частиц):

Уравнение теплопроводности (закон сохранения энергии):

Здесь k - теплопроводность [Вт/(м·К)], C - удельная теплоемкость [Дж/(м³·К)], Q - объемный источник тепла [Вт/м³].

Уравнение Навье-Стокса (закон сохранения импульса), для x-компоненты скорости, приближение несжимаемой среды:

Здесь η - динамическая вязкость [Па·с], ρ_gd - плотность среды [кг/м³], P - давление [Па].

Уравнение диффузии

В одномерном случае:

Рассмотрим набор узлов x₁, x₂, ... x_n. Расстояние между соседними узлами равно h:

x_j-x_j-1=h

(1)

Для анализа на устойчивость представим искомую функцию в виде некоторого решения R(x,t) и возмущения ε(x,t):

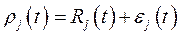
Поскольку R_j(t) - решение, для него выполнено:

Подставим решение с возмущением в уравнение (1):

(2)

Поскольку уравнение линейное однородное, его можно разложить в ряд Фурье. Поэтому рассмотрим одну Фурье-компоненту:

В начальный момент времени:

Любое начальное возмущение можно разложить в ряд по таким "элементарным" возмущениям с разными волновыми числами k.

Подставляя "элементарное" возмущение в уравнение (2), получаем:

Любое возмущение затухает:

Таким образом, уравнение диффузии безусловно устойчиво по отношению к пространственным возмущениям.