Корни многочлена и схема Горнера. Полиномы над числовыми полями
Комплексные числа
- Вычислить: (2+3i)(4–5i) + (2–3i)(4+5i).
- Найти х и у, считая их действительными числами: (1+2i)x + (3–5i)y = 1–3i
- Вычислить, пользуясь формулой Муавра:
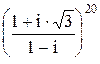 .
. - Извлечь все корни: 1)
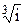 . 2)
. 2) 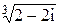 . 3)
. 3) 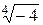 . 4)
. 4) 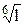 .
. - Выполнить действия:
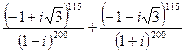 .
.
Теория делимости
- Вычислить НОД(588, 2058, 2849) двумя способами.
- Вычислить НОД(99, 162) двумя способами.
- Построить графики функций:
а) y=j (x), б) y=t(x), в) y= s(x), где x Î N.
14. Вычислить j (x),t(x), s(x), где x=588, x= 2058 .
Системы линейных уравнений
- Решить систему линейных уравнений методом последовательного исключения переменных:
1)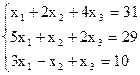 2)
2) 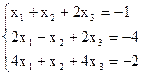
3)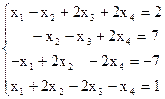 4)
4) 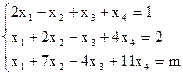
5)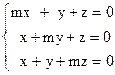 6)
6) 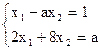 .
. - Решить систему линейных уравнений с помощью обратной матрицы и методом Крамера
1) 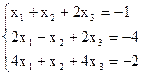 2)
2) 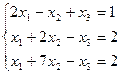
Линейные системы векторов. Векторные пространства.
11. Исследовать, является ли линейно зависимой система векторов 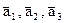 :
:
1) 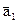 =(1, 2, 1), 2)
=(1, 2, 1), 2) 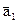 =(1,–2,–1),
=(1,–2,–1),
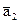 =(1, 1,–1),
=(1, 1,–1), 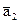 =(–1, 1,–1),
=(–1, 1,–1),
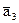 =(–1,–3,–3).
=(–1,–3,–3). 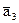 =(–1,–3,–3).
=(–1,–3,–3).
12. Исследовать, является ли линейно зависимой система векторов 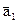 ,
, 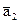 векторного пространства многочленов от одной переменной степени £ 2 над полем R, если
векторного пространства многочленов от одной переменной степени £ 2 над полем R, если
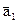 =f1(x)=3+x+2x2,
=f1(x)=3+x+2x2, 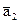 =f2(x)=–2+x–x2.
=f2(x)=–2+x–x2.
- Доказать, что в вещественном пространстве квадратных матрицах второго порядка первый из трех векторов
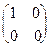 ,
, 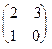 ,
, 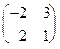 не выражается линейно через остальные.
не выражается линейно через остальные. - Подпространство V0 натянуто на систему векторов
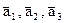 , где
, где
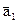 =(1, 2, 1),
=(1, 2, 1), 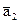 =(1, 1,–1),
=(1, 1,–1), 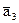 =(1, 3, 3). Найти базис и размерность V0.
=(1, 3, 3). Найти базис и размерность V0. - Найти размерность и базис линейных подпространств, натянутых на следующие системы векторов:
1) 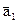 =(1,0,0,-1),
=(1,0,0,-1), 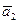 =(2,1,1,0),
=(2,1,1,0), 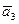 =(1,1,1,1),
=(1,1,1,1), 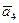 =(1,2,3,4),
=(1,2,3,4), 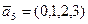 ,
,
2) 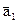 =(1,1,1,-1,0),
=(1,1,1,-1,0), 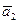 =(1,1,-1,-1,-1),
=(1,1,-1,-1,-1), 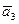 =(2,2,0,0,-1),
=(2,2,0,0,-1), 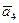 =(1,1,5,5,2),
=(1,1,5,5,2), 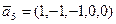 .
.
- Вычислить ранг матрицы
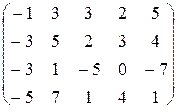 ;
; 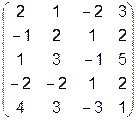 .
.
17. Найти один из базисов данной системы векторов и выразите остальные векторы системы через базисные, если 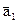 =(1, 2, 1),
=(1, 2, 1), 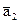 =(1, 1,–1),
=(1, 1,–1), 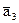 =(–1,–3,–3),
=(–1,–3,–3), 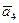 =(–1,–3,–3).
=(–1,–3,–3).
18. Векторы 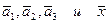 заданы своими координатами в некотором базисе. Показать, что векторы
заданы своими координатами в некотором базисе. Показать, что векторы 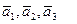 сами образуют базис, и найти координаты вектора
сами образуют базис, и найти координаты вектора 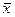 в этом базисе:
в этом базисе: 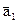 =(1, 1, 1),
=(1, 1, 1), 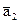 =(1, 1,2),
=(1, 1,2), 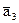 =( 1, 2, 3),
=( 1, 2, 3), 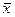 =( 6,9,14).
=( 6,9,14).
Найти базис и размерность векторного пространства V над полем R, состоящего из всех матриц вида , где a, b, c, dÎR.
Матрицы и определители
- Умножить матрицы:
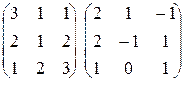 ,
, - Найти
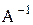 , если А=
, если А= 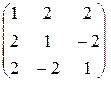 .
. - Решить матричное уравнение: 1)
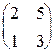 ×X =
×X = 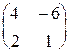 2)
2) 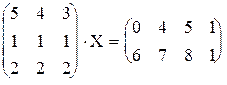
- Вычислить: 1)
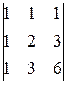 , 2)
, 2) 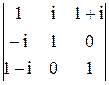
- Вычислить определитель матрицы, разложив по строке или столбцу:
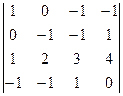 ,
,
Полиномы от одной переменной. Наибольший общий делитель и наименьшее общее кратное двух полиномов
- Разложить многочлен f(x)=x12–2x6+1 на неприводимые множители над полем действительных и комплексных чисел.
- Найти остаток от деления f на g, пользуясь схемой Горнера: f=x4–2x3+4x2–6x+8, g=x–1.
- Найти НОД и НОК: f1=x3+2x2+3x +2, f2=x4+x3+x2–x–2, f3=x3–x2–4.
- Найти НОД многочленов f(x) и g(x):
1) f(x)=x6+x5–3x4+2x3+4x–2, g(x)=x5+3x4+x3+6x2+4x+6.
2) f(x)=(x–1)813(x+2)107(x–3)91 , g(x)=x9+x8–5x7+x6+11x5–13x4–7x3+15x2–4. - Для многочленов f=x3–x2+3x–10 и g=x3+6x2–9x–14 найти такие многочлены u и v, что f·u+g·v=d, где d=НОД(f,g).
- Найти НОД(f,g) и его линейное представление через f и g: f=x3+x2-x–1, g=x4+x3-3x2-4x-1.
- Найти НОД(f,g) , НОК[f,g] и линейное представление НОД через f и g : f=x4–4x3+1, g=x3–3x2+1.
Корни многочлена и схема Горнера. Полиномы над числовыми полями
- Найти кратность корня c = –2 у многочлена f, если f=x5+6x4+11x3+2x2–12x–8.
- Разложить f по степеням двучлена x+2, если f=3x5+7x4+x3–2x+3 (с помощью схемы Горнера).
- Отыскать рациональные корни многочлена f(x):
1) f(x)=x4-2x3-8x2+13x-24,
2) f(x)=10x4-13x3+15x2-18x-24,
Основные понятия теории групп. Кольца и поля.
- Доказать, что множество целых чисел, кратных 3, есть подгруппа аддитивной группы целых чисел.
- Доказать, что множество матриц вида
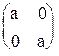 , где аÎR \ {0}, есть подгруппа мультипликативной группы G всех невырожденных матриц второго порядка.
, где аÎR \ {0}, есть подгруппа мультипликативной группы G всех невырожденных матриц второго порядка. - Доказать, что отображение x ® 3x является изоморфизмом аддитивной группы действительных чисел на мультипликативную группу положительных действительных чисел.
- Исследовать, образует ли кольцо относительно операций сложения и умножения матриц множество М матриц вида
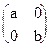 , где a, b- любые действительные числа.
, где a, b- любые действительные числа. - Проверить, образует ли поле кольцо <A,+,•> , если A=
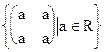 .
. - Проверить, отображение j, такое, что
j: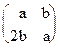 →
→ 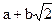 , является ли изоморфизмом поля F1 на поле F2, где F1=
, является ли изоморфизмом поля F1 на поле F2, где F1= 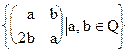 , F2=Q(
, F2=Q( 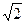 )=
)= 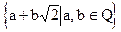 , а операции определены как обычно.
, а операции определены как обычно.
