Определение коэффициента вязкости жидкости по методу Стокса

Цель работы: определить коэффициент вязкости жидкости по методу Стокса.

Необходимые приборы и принадлежности: стеклянный цилиндр

наполненный глицерином, свинцовые шарики, микрометр, секундомер и линейка.

Теоретическое введение

Всем реальным жидкостям и газам в большей или меньшей

степени присуще внутреннее трение, называемое также вязкость.

В жидкостях внутреннее трение обусловлено действием межмолекулярных сил.

Расстояние между молекулами жидкости сравнительно невелики, а силы взаимодействия значительны. Молекулы жидкости, подобно частицам твердого тела, колеблются около положения равновесия, по истечении некоторого времени молекула скачком переходит в новое положение. Это время называется временем ''оседлой жизни" молекулы. Среднее время "оседлой жизни" молекул называется временем релаксации. С повышением температуры и понижением давления время релаксации уменьшается, что обусловливает подвижность жидкости и ее малую вязкость. Зависимость вязкости жидкости от температуры имеет сложный характер; чем чаще молекулы меняют свое положение равновесия, тем более текуча и менее вязка жидкость, Т. е. вязкость жидкости прямо пропорционально времени релаксации.

Механизм возникновения сил внутреннего трения ( вязкости), с точки зрения молекулярно – кинетической теории заключается в следующем. В потоке жидкости молекулы участвуют одновременно в двух движениях: хаотическом тепловом, средняя скорость которого равна 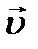, и упорядоченном движении со скоростью потока 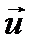. Скорость 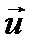намного меньше, чем 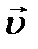, т.е. ( 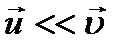). При рассмотрении внутреннего трения нас будет интересовать средний импульс молекулы в потоке жидкости .

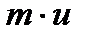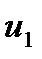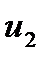
Предположим, что имеются два соприкасающихся слоя жидкости, движущихся параллельно друг другу с различными скоростями и . При перемещении одних слоев реальной жидкости относительно других, возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.

Пусть в некоторый момент времени слои обладают импульсам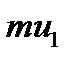и и 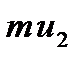. Вследствии теплового движения происходит непрерывный переход молекул из одного слоя в другой. Попав в другой слой, молекула претерпевает столкновения с молекулами этого слоя, в результате чего она либо отдает избыток своего импульса другим молекулам (если она прилетела из слоя, движущегося быстрее), либо увеличивает свой импульс за счет других молекул ( если она “прилетела” из слоя, движущегося медленнее). В итоге импульс слоя, движущегося быстрее убывает, а слоя, движущегося медленнее, возрастает. Следовательно, слои ведут себя так, как если бы к слою, скорость которого больше, была приложена сила тормозящая его движение, а к слою скорость которого меньше – такая же по модулю сила, ускоряющая его движение. Таким образом, причиной возникновения вязкости ( внутреннего трения) является перенос импульса от одного слоя к другому. Экспериментально установлено, что модуль силы внутреннего трения, приложенный к площадке 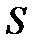, лежащий на границе между слоями определяется формулой

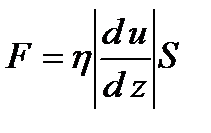(1)

где 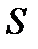– площадь на границе между слоями поверхности, на которой действует сила 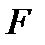. Величина 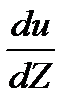– показывает, как быстро меняется скорость при переходе от слоя к слою в направлении 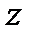, перпендикулярном направлению движения слоев, и называется градиентом скорости. В этой формуле 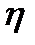– коэффициент пропорцианальности, зависящий от природы и состояния жидкости, называется вязкостью.

Это уравнение (1) было установлено Ньютоном в 1687г и называется законом Ньютона. Согласно второму закону Ньютона сила равна производной импульса по времени. Поэтому уравнение (1) можно представить в виде

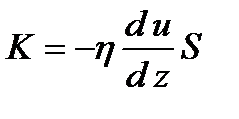(2)

где 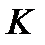- импульс, передаваемый от слоя к слою, т.е. поток импульса через поверхность 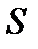. Знак минус в этой формуле обусловлен, тем обстоятельством, что импуль “течет” в направлении убывания скорости

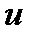. Поэтому знаки потока импульса и производной 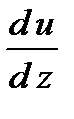противоположны. Здесь вязкость показывает, какое количество импульса (поток импульса) переносится через единицу площади за единицу времени при градиенте скорости, равном единице.

Вязкость измеряется в килограммах на метр секунду 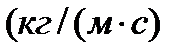или в паскаль–секундах 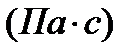т.е. 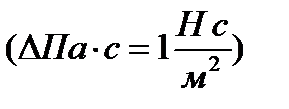. Экспериментальную формулу Ньютона (2) можно вывести с помощью молекулярно – кинетической теории. При этом получается выражение для вязкости

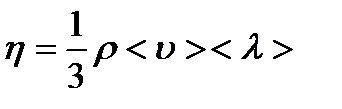(3)

здесь 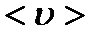– средняя скорость теплового движения молкул, 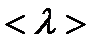– средняя длина свободного пробега молекул, 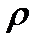– плотность жидкости или газа. Вязкость является важной физико- технической характеристикой вещества и зависит от температуры и от природы вещества. С повышением температуры вязкость уменьшается.