Признаки возрастания и убывания функции. асимптоты

Признаки возрастания и убывания функции

Определение 8.1.Функция у = f (x) на интервале ( ) называется:

а) постоянной, если f (x) = c, где с = const, для любого х Î ( );

б) возрастающей,если для любых двух значений х₁, х₂ Î ( ) из неравенства х₁ < х₂ следует неравенство f (x₁) < f (x₂);

в) убывающей,если для любых двух значений х₁, х₂ Î ( ) из неравенства х₁ < х₂ следует неравенство f (x₁) > f (x₂).

Теорема 8.1. (достаточное условие возрастания и убывания функции).

Если в данном промежутке производная функции положительна, то функция возрастает в этом промежутке; если производная отрицательна, то функция убывает в соответствующем промежутке; если же производная равна нулю, то функция постоянна на промежутке.

Доказательство.Рассмотрим функцию y = f (x) на ( ). Возьмём произвольно х₁, х₂ Î ( ) такие, что х₁ < х_2. По теореме Лагранжа

f (x₂) – f (x₁) = f '(c)(x₂ − x₁), где с Î (х₁; х₂).

Возможны следующие случаи:

1) производная f '(x) > 0 на ( ). Тогда f '(c) > 0, x₂ − x₁ > 0 и поэтому f (x₁) – f (x₂) > 0, т. е. f (x₁) < f (x₂). Следовательно, f (x) возрастает на ( );

2) производная f '(x) > 0 на ( ). Тогда f '(c) > 0, x₂ − x₁ > 0 и поэтому f (x₁) – f (x₂) < 0, т. е. f (x₁) > f (x₂). Следовательно, функция у = f (x) убывает на ( );

3) производная f '(x) = 0 на ( ). Тогда f '(c) = 0, откуда f (x₁) – f (x₂) = 0, т. е. f (x₁) = f (x₂).

Это означает, что функция у = f (x) постоянна на ( ).

Асимптоты

Если график функции сколь угодно близко приближается к прямой, то такую прямую называют асимптотой. Различают вертикальные и наклонные асимптоты.

Определение 8.2.Прямая х = 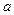называется вертикальной асимптотойграфика у = f (x), если хотя бы одно из предельных значений 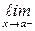f (x), 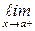f (x) является бесконечным.

Например, прямая х = 2 – вертикальная асимптота графика у = 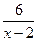, так как = −¥, = +¥.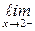

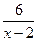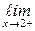
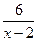Определение 8.3.Предположим, что функция у = f (x) определена при сколь угодно больших (по модулю) значениях аргумента. Для определённости будем рассматривать положительные значения аргумента. Прямая

у =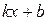

называется наклонной асимптотойграфика функции у = f (x), если эта функция представима в виде

f (x) = ,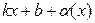

где 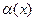– бесконечно малая функция при х → +¥.

Теорема 8.2. (необходимые и достаточные условия существования асимптоты).

График функции у = f (x) имеет при х → +¥ наклонную асимптоту у = 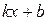тогда и только тогда, когда существуют два конечных предела

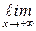
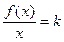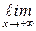
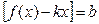, . (8.1)

Доказательство.Пусть график функции у = f (x) имеет асимптоту у = 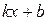. Тогда f (x) = 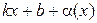, где 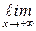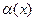= 0. Следовательно,

,

.

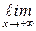
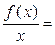
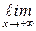
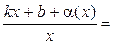
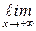
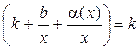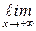
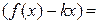
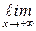
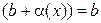Обратно. Пусть существуют пределы (8.1). Тогда из равенства 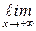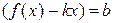можем записать также, что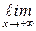 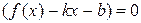. Это означает, что функция 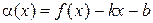является бесконечно малой функцией при х → +¥. Отсюда f (x) = 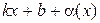и по определению прямая у = 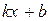является наклонной асимптотой.

Пример 8.1.Рассмотрим функцию у = .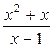

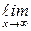
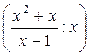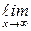
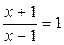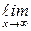
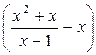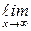
Так как = и = 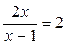, то график функции имеет наклонную асимптоту у = .

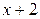Экстремум функции.