Применение первой производной к исследованию графика функции

.

4.15.1Признаки возрастания и убывания функции.

Если первая производная у ¢( х) > 0 на интервале ( а,b ), то функция у(х) возрастает на этом интервале.

Если первая производная у ¢(х) < 0 на интервале ( а,b), то функция у(х) убывает на этом интервале.

Необходимое и достаточное условия экстремума

Необходимое условие экстремума функции: Теорема Ферма. Если точка х₀ является точкой экстремума функции и в этой точке существует производная, то у¢(х) = 0 .

Экстремум функции – это либо максимум функции, либо минимум функции. Касательная к графику функции в точке экстремума параллельна оси абсцисс.

Достаточное условие экстремума функции:

Если производная у¢ при переходе через точку х₀ меняет знак с «+»на«-», то точка х₀ является точкой максимума.

Если производная у¢ при переходе через точку х₀ меняет знак с «-» на

«+», то точка х₀ является точкойминимума.

Если знак производной не меняется, то функция в точке не имеет ни максимума ни минимума.

Точки, в которых производная функции обращается в ноль или не существует ( то есть стремится к бесконечности), называются критическими точками первого рода.

4.15.3. Первое правило нахождения экстремумов

1. Найти производную f ¢(х).

2. Найти действительные корни уравнения f ¢(х) = 0.

3. Расположить корни уравнения х_1, х₂ … х_n в порядке возрастания на числовой оси, в результате ось разобъется на интервалы. В каждом интервале определить знак производной.

4. Выяснить какие корни являются точкой максимума, точкой минимума и какой корень не является точкой экстремума.

5. Найти значения функции в точках экстремумов.

Применение второй производной к исследованию графика

Функции

4.16.1. Второе правило нахождения экстремумов

1. Найти производную f¢ (х).

2. Найти корни уравнения f ¢(х) = 0 ® х₁ , х₂ ,…

3. Найти вторую производную f ² (х).

4. Если f ² (х₁) < 0 , то в этой точке максимум,

f ² (х₁) > 0, то в этой точке минимум,

f ² (х₁) = 0, то нужно обращаться к первому правилу.

Выпуклость и вогнутость кривой

Если вторая производная у¢¢(х) > 0 на интервале ( а, b). то график функции у(х) является вогнутой кривой на этом интервале, то есть он расположен выше любой касательной, проведенной к графику функции в точках этого интервала.

Если вторая производная у¢¢(х) < 0 на интервале ( а,b), то график функции у(х) является выпуклой кривой на этом интервале, то есть он расположен ниже любой касательной, проведенной к графику функции в точках этого интервала.

Точка, в которой вторая производная у¢¢(х) = 0 и при этом вторая производная меняет знак при переходе через эту точку, называется точкой перегиба графика функции.

Точки, в которых вторая производная равна нулю или не существует (то есть стремится к бесконечности), называются критическими точками второго рода.

Пример 4 Для выполнения контрольного задания №2

Исследовать функцию у = х² – 16х на максимум и минимум с помощью первой производной, исследовать функцию на выпуклость и вогнутость

с помощью второй производной функции.

Решение

1. Найти производную данной функции:

у ¢ = 2х – 16

2. Приравнять производную к нулю и найти корни (критические точки) уравнения: у ¢= 0, 2х – 16 = 0, отсюда х = 8. Для удобства вынесем множитель 2:

2( х – 8) = 0.

3. Выясним, как производная меняет знак при переходе через точку х = 8

Возьмем значение х < 8, например, 7 и подставим в уравнение и найдем знак производной. Знак производной получился « - ». Значит, функция убывает при х<8.

Возьмем значение х > 8, например, 9 и подставим в уравнение и найдем знак производной, Знак производной получился «+». Значит, функция возрастает при х>8.

Производная меняет знак с « - » на «+» (с минуса на плюс), следовательно функция имеет минимум в точке х = 8.

4. Найдем минимальное значение функции в критической точке:

у = 8² – 128 = 64 – 128 = - 64.

Точка минимума функции (8, - 64) является вершиной параболы, а ветви параболы направлены вверх.

5. Найдем производную второго порядка, для этого продифференцируем первую производную, которая равна у ¢= 2х -16. у ¢¢ = 2. Вторая производная больше нуля, следовательно график функции является вогнутой кривой при всех значениях х.

4.17. Уравнениякасательнойинормали

Уравнениекасательной к данной кривой у = f(х), проходящей через точку на ней М (х₁, у₁) имеет вид:

у – у₁ = f ¢ (х₁) (х – х₁),

где угловой коэффициент k₁ в точке х₁ равен производной функции в этой точке.

Нормалью к кривой у = f(х) в данной её точке М(х₁,у₁) называется перпендикуляр к касательной, проведенный через точку касания М. Угловой коэффициент в уравнении нормали к кривой имеет вид:

k₂ = -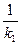

4.18. Асимптотыкривой

Прямая y=kx + b называется наклонной асимптотой кривой y =f(x) при х ® +¥, если

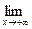( f (x) – kx –b) = 0

Отсюда, k = 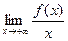, b = .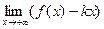

Если k = 0, то уравнение асимптоты имеет вид: у = b (горизонтальная асимптота).

Прямая х = а называется вертикальной асимптотой, если односторонние пределы функции в этой точке равны бесконечности. Обычно это точки разрыва второго рода.

4.19. Общаясхема исследования функций

1. Найти область определения функции;

2. исследовать функцию на четность и нечетность;

3. исследовать функцию на периодичность;

4. исследовать функцию на непрерывность, найти точки разрыва. Для этого приравнять знаменатель к нулю, найти значения х, при которых знаменатель обращается в ноль. В этих точках график функции терпит разрыв.

5. найти критические точки первого рода. Для этого найти первую производную, приравнять её к нулю, решить уравнение и найти действительные корни уравнения;

6. найти интервалы монотонности и экстремумы функции. Для этого методом проб определяются знаки производной в каждом из интервалов;

7. найти критические точки второго рода. Для этого найти вторую производную и приравнять её к нулю. Из этого уравнения находят критические точки второго рода. Кроме этого находят еще критические точки, где вторая производная не существует

8. найти интервалы выпуклости и точки перегиба. Для этого определяют знак второй производной в каждом интервале.

9. найти асимптоты графика функции. Для этого по формулам находят коэффициенты уравнения асимптоты, затем строят линии асимптот.

10. найти точки пересечения с осями координат;

11. построить график функции.

Контрольное задание №2

14 вариантов

Найти производные от произведения двух функций и записать

дифференциалы:

1. y = х² sin x 8. у = sin x cos x

2. y = x³ ×cosx 9. y = e ^х sin x

3. y = x× tgx 10. y = lnx× sin x

4. y = x⁵ e^x 11. y = 2 ^х ×cos x

5. y = x² ×lnx 12. y = e^х ×cosx

6. y = x ³ 2^х 13. y = tgx× e^х

7. y = x² ×ctgx 14. y = 3^х × e^х

Найти производные частного двух функций :

1. у = sinx/ x² 8. y = sinx/cosx

2. y = cosx/ x³ 9. y = cosx/sinx

3. y = tgx/ x 10. y = e ^x / sinx

4. y = e^x / x³ 11. y = 3 ^x / cosx

5. y = 2 ^х / x 12. y = tgx/ 2^x

6. y = lnx/ x³ 13. y = x ⁴ / 2 ^x

7. y = x⁵ /sinx 14. y = x/ sinx

Найти скорость и ускорение прямолинейного движения материальной точки в момент времени t:

1. S = 3t + t³ + 7 t = 3 8. S = 2t³ + 4t² + 5 t = 1

2. S = 4 + 2t + t⁴ t = 1 9. S = 3t² + t³ + 6 t = 2

3. S = 9 + 3t + 2t³ t = 3 10. S = 3t³ + 4t² + 5 t = 1

4. S = 8 + t² + 2t³ t = 2 11. S = 5t² + 2t³ + 9 t = 2

5. S = 9 + 2t² + t³ t = 2 12. S = 4t² + 8 + t³ t = 3

6. S = 5t² + 4t³ t = 3 13. S = t³ + 9 + 3t² t = 2

7. S = 7 + t³ + 5t² t = 4 14. S = t⁴ + 8 + 4t t = 2

Исследовать функцию на экстремум, исследовать функцию на точки перегиба:

1. у = (х + 2)² (х – 4)

2. у = (х + 3)² (х - 6)

3. у = (х + 4)² (х – 5)

4. у = (х + 1)² (х - 5)

5. у = (х - 5 )² (х + 1)

6. у = (х + 2)² (х – 7)

7. у = ( х – 2)² (х – 5)

8. у = (х -7)² (х + 2)

9. у = (х + 5)² (х – 4)

10. у = (х – 8)² (х + 1)