Методы среднесрочного прогнозирования

Применяются в следующих случаях:1)имеются ежегодные данные 2) прогноз осуществляется для временных рядов относительно малой длинны. Метод линейной регрессии оказывается достаточно надежным.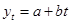

b-коэффициент регрессии он характеризует наклон линии регрессии. а-начальный или свободный коэффициент, характеризует уровень пересечения осью y.

b=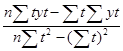

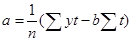
Для определения значимости характеристик необходимо определить насколько хорошо уравнение регрессии объясняет дисперсию зависимой переменной в зависимости от t по сравнению с общей дисперсией.

Общая дисперсия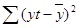

Объясняемая дисперсия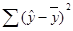

Остаточная дисперсия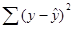

r² коэффициент детерминации определяет как доля общей дисперсии объясняется регрессии.

r коэффициент корреляции определяет тесноту связи между переменными.

Для прогнозирования с помощью регрессии необходимо вместо t подставить нужный уровень ряда и произвести расчет. Доверительный интервал ! это интервал, в который с определенной степенью уверенности можно ожидать появление фактического значения прогнозируемой переменной. Определяется по формуле

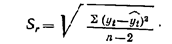-стандартная ошибка.

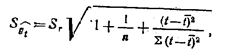- ошибка прогноза.

После нахождения стандартной ошибки прогноза можно определить доверительные интервалы: приближенными 99, 95 и 68% ными доверительными интервалами будут 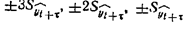соответственно.

На практике прогноз может быть осуществлен не только с помощью линейной зависимостью, для этого необходимо произвести линеанелизацию

На практике встречаются данные которые могут быть описаны кривыми имеющими точку перегиба. В таких случаях используют кривую Гомперца и лигистическую кривую. Для оценки параметров их сводят к модифицированной экспоненте.

Параметры определяют по формулам.

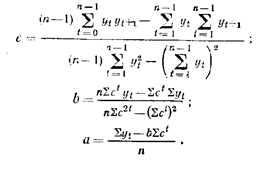
Метод кумулятивных сумм.

Одной из причин уменьшения точности прогноза является сдвиги в данных прогнозируемых показателей, один из методов распознания данных сдвигов - метод кумулятивных сумм – вычисление кумулятивной суммы ошибок. Для каждого уровня ряда вычисляется отклонение прогнозируемого показателя от фактического. Эта процедура приведет к серии положительных и отрицательных ошибок, суммирование этих ошибок приведет к величине CUSUM. Если график кумулятивной суммы растет значит произошел сдвиг в динамике у ровня в положительную сторону. Если падает отрицательную. По скорость подъема графика можно судить о размере сдвига.

Метод кумулятивных сумм может быть выражен с подошью 2-х формул:

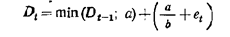
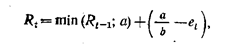
Где а и b параметры, е – текущая ошибка.

Если D становиться отрицательным произошло понижение среднего уровня,

Если R – повышение. Параметры a и b подбираются имперически.