Функции нескольких переменныХ
Пример 9. Фирма производит товар двух видов в количестве x и y соответственно. Функция полных издержек определена соотношением 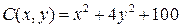 .
.
Построить на плоскости Oxy множество производственных возможностей, определяемое ограничением на издержки в объеме 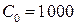 ден. ед.
ден. ед.
Решение. множество производственных возможностей задается системой неравенств:
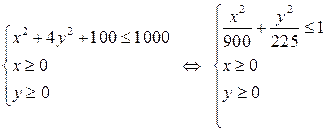
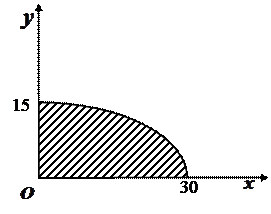 |
и является криволинейным треугольником, ограниченным на плоскости Oxy четвертью эллипса с полуосями
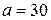 ;
; 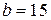 и осями координат.
и осями координат. Задача 9.Полные издержки фирмы, производящей товар двух видов в количестве x и y соответственно, заданы функцией 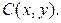
Построить на плоскости Oxy множество производственных возможностей, определяемое ограничением на издержки в объеме С0:
9.1. 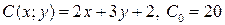 ;
;
9.2. 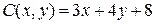 ,
, 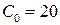 ;
;
9.3. 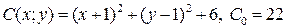 ;
;
9.4. 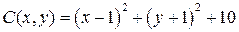 ,
, 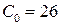 ;
;
9.5. 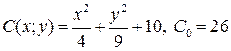 ;
;
9.6. 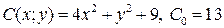 ;
;
9.7. 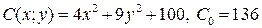 ;
;
9.8. 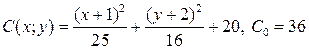 ;
;
9.9. 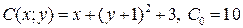 ;
;
9.10. 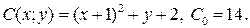
Пример 10.1. Производственная функция однопродуктовой фирмы, использующей два вида ресурсов, имеет вид 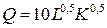 .
.
Построить изокванты, соответствующие значениям объема выпуска продукции в объемах: 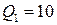 ед.,
ед., 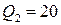 ед. и
ед. и 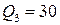 ед.
ед.
Решение. Изокванта – линия постоянного выпуска. Уравнение изокванты: 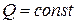 . Возведем обе части уравнения
. Возведем обе части уравнения 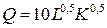 в квадрат. получим
в квадрат. получим 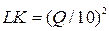 . Для изокванты
. Для изокванты 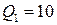 имеем уравнение
имеем уравнение 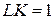 , или
, или 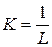 . Аналогично для изокванты
. Аналогично для изокванты 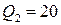 имеем уравнение
имеем уравнение 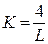 , а для изокванты
, а для изокванты 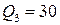 получаем уравнение
получаем уравнение 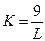 . Графики этих изоквант
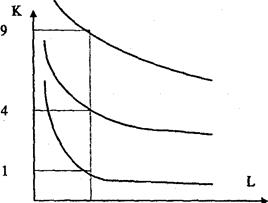
. Графики этих изоквант 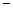 части гипербол, расположенные в первой четверти:
части гипербол, расположенные в первой четверти:
Пример 10.2. Производственная функция однопродуктовой фирмы, использующей два вида ресурсов, имеет вид 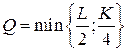 .
.
Построить изокванты, соответствующие значениям объема выпуска продукции в объемах: 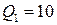 ед.,
ед., 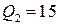 ед. и
ед. и 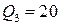 ед.
ед.
Решение. Изокванты производственной функции 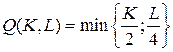 определяются условием
определяются условием
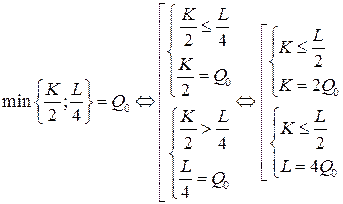
и представляют собой «уголки», скользящие по прямой 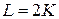 . Графики этих изоквант изображены ниже.
. Графики этих изоквант изображены ниже.
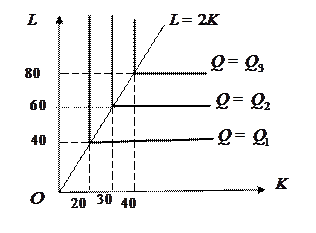 |
Вершина изокванты
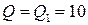 имеет координаты
имеет координаты 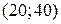 , вершина изокванты
, вершина изокванты 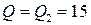 имеет координаты
имеет координаты 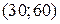 , вершина изокванты
, вершина изокванты 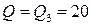 имеет координаты
имеет координаты 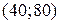 .
. Задача 10.Задана производственная функция 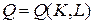 однопродуктовой фирмы, использующей два вида ресурсов.
однопродуктовой фирмы, использующей два вида ресурсов.
Построить изокванту, соответствующую значению объема выпуска продукции 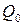 ед.
ед.
10.1. 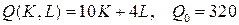 ; ; | 10.6. 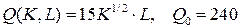 ; ; |
10.2. 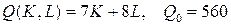 ; ; | 10.7. 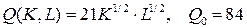 ; ; |
10.3. 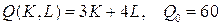 ; ; | 10.8. 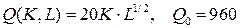 ; ; |
10.4. 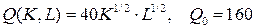 ; ; | 10.9. 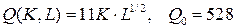 ; ; |
10.5. 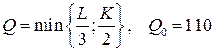 ; ; | 10.10. 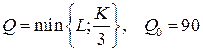 . . |
Пример 11. Производственная функция однопродуктовой фирмы, использующей два вида ресурсов, имеет вид 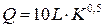 .
.
Найти предельную производительность труда 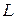 и капитала
и капитала 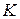 .
.
Решение. Предельная производительность труда вычисляется по формуле 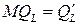 , а предельная производительность капитала по формуле
, а предельная производительность капитала по формуле 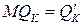 . Вычисляя частные производные функции двух переменных
. Вычисляя частные производные функции двух переменных 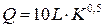 , получаем
, получаем 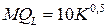 и
и 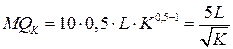 .
.
Ответ: 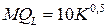 ,
, 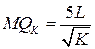 .
.
Задача 11.Задана производственная функция 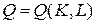 однопродуктовой фирмы, использующей два вида ресурсов.
однопродуктовой фирмы, использующей два вида ресурсов.
Найти предельную производительность труда 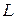 и капитала
и капитала 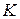 .
.
10.1. 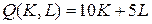 ; ; | 10.6. 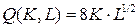 ; ; |
10.2. 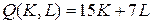 ; ; | 10.7. 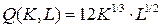 ; ; |
10.3. 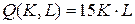 ; ; | 10.8. 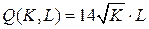 ; ; |
10.4. 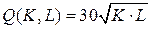 ; ; | 10.9. 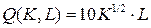 ; ; |
10.5. 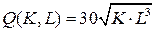 ; ; | 10.10. 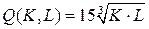 . . |
Пример 12. Производственная функция однопродуктовой фирмы, использующей два вида ресурсов, имеет вид 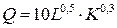 .
.
Найти коэффициент эластичности производственной функции по труду 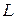 и по капиталу
и по капиталу 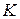 .
.
Решение. Формулы для вычисления коэффициента точечной эластичности функции 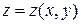 по переменным
по переменным 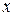 и
и 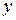 имеют вид
имеют вид 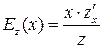 и
и 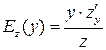 соответственно. Для производственной функции
соответственно. Для производственной функции 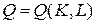 коэффициент эластичности производственной функции по капиталу будет вычисляться по формуле
коэффициент эластичности производственной функции по капиталу будет вычисляться по формуле 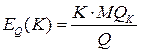 , а коэффициент эластичности по труду
, а коэффициент эластичности по труду 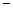 по формуле
по формуле 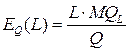 .
.
Для заданной производственной функции 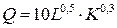 получаем
получаем
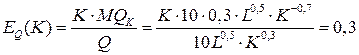 и
и
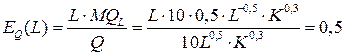 .
.
Задача 12.Производственная функция однопродуктовой фирмы, использующей два вида ресурсов, имеет вид 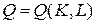 .
.
Найти коэффициент эластичности производственной функции по труду 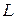 и капиталу
и капиталу 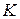 .
.
12.1. 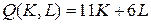 ; ; | 12.6. 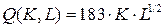 ; ; |
12.2. 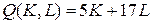 ; ; | 12.7. 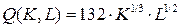 ; ; |
12.3. 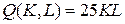 ; ; | 12.8. 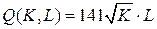 ; ; |
12.4. 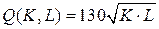 ; ; | 12.9. 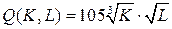 ; ; |
12.5. 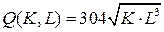 ; ; | 12.10. 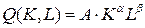 . . |
Пример 13. Функция полезности потребителя двух товаров, приобретаемых им в количествах x и y соответственно, задана соотношением 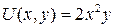 .
.
Найти предельную норму замещения первого товара вторым.
Решение. Предельная норма замещения первого товара вторым показывает, на сколько надо увеличить потребление второго товара при уменьшении потребления первого товара на единицу. Формула для вычисления предельной нормы замещения первого товара вторым имеет вид 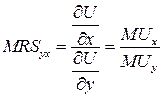 , где
, где 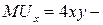 предельная полезность первого товара, а
предельная полезность первого товара, а 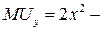 предельная полезность второго товара. Таким образом,
предельная полезность второго товара. Таким образом, 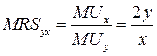 .
.
Ответ: 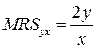 .
.
Задача 13.Функция полезности потребителя двух товаров, приобретаемых им в количествах x и y соответственно, задана соотношением 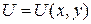 .
.
Найти предельную норму замещения 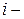 го товара
го товара 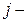 ым товаром.
ым товаром.
13.1. 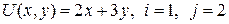 ; ; | 13.6. 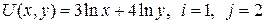 ; ; |
13.2. 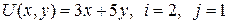 ; ; | 13.7. 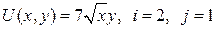 ; ; |
13.3. 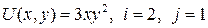 ; ; | 13.8. 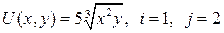 ; ; |
13.4. 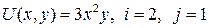 ; ; | 13.9. 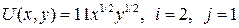 ; ; |
13.5. 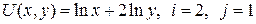 ; ; | 13.10. 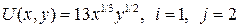 . . |
Пример 14. Функция полных издержек фирмы, производящей товар двух видов в количествах x и y, задана соотношением 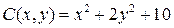 . Цены этих товаров на рынке равны соответственно
. Цены этих товаров на рынке равны соответственно 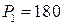 ден. ед. и
ден. ед. и 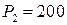 ден. ед.
ден. ед.
Определить, при каких объемах выпуска достигается максимальная прибыль 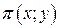 и чему она равна.
и чему она равна.
Решение. Функция прибыли 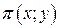 равна разности функций дохода
равна разности функций дохода 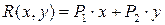 и функции полных издержек
и функции полных издержек 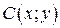 :
:
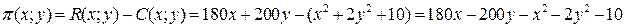 .
.
Выпишем необходимое условие экстремума функции двух переменных:
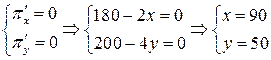 .
.
Таким образом, 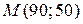 ‑ стационарная точка, точка возможного экстремума.
‑ стационарная точка, точка возможного экстремума.
Проверим достаточные условия максимума. Для этого найдем производные второго порядка:
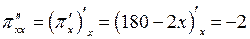 ;
;
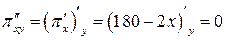 ;
;
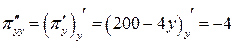 .
.
Вычислим: 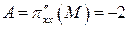 ;
; 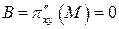 ;
; 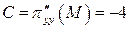 и
и
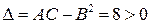 . Следовательно, точка
. Следовательно, точка 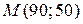 является точкой экстремума функции, а так как
является точкой экстремума функции, а так как 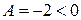 , то точка
, то точка 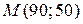 является точкой локального максимума.
является точкой локального максимума.
Имеем: 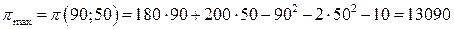 .
.
Ответ: 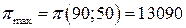 .
.
Задача 14.Функция полных издержек фирмы, производящей товар двух видов в количества x и y, задана соотношением 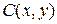 . Цены этих товаров на рынке равны соответственно
. Цены этих товаров на рынке равны соответственно 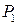 ден. ед. и
ден. ед. и 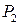 ден. ед.
ден. ед.
Определить, при каких объемах выпуска достигается максимальная прибыль 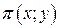 и чему она равна.
и чему она равна.
14.1. 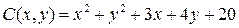 ;
; 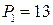 ;
; 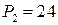 ;
;
14.2. 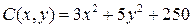 ;
; 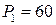 ;
; 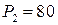 ;
;
14.3. 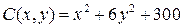 ;
; 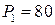 ;
; 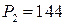 ;
;
14.4. 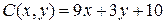 ;
;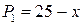 ;
;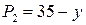 ;
;
14.5. 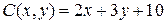 ;
; 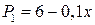 ;
;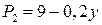 ;
;
14.6. 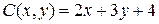 ;
; 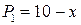 ;
;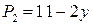 ;
;
14.7. 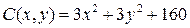 ;
; 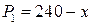 ;
;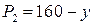 ;
;
14.8. 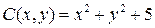 ;
; 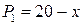 ;
;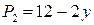 ;
;
14.9. 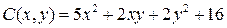 ;
; 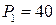 ;
; 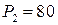 ;
;
14.10. ;; .
Пример 15. функция полезности потребителя двух товаров, приобретаемых в количествах 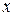 и
и 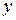 соответственно, имеет вид
соответственно, имеет вид 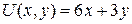 .
.
Определить объем оптимальной покупки, если доход потребителя 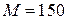 ден. ед., цены на покупаемые товары равны соответственно
ден. ед., цены на покупаемые товары равны соответственно 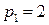 ден. ед.,
ден. ед., 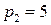 ден. ед. и на рынок поступает не более
ден. ед. и на рынок поступает не более 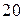 единиц товара первого вида.
единиц товара первого вида.
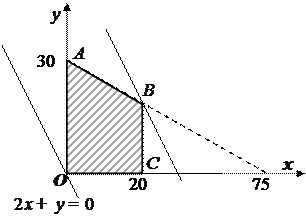
Решение. Бюджетное множество потребителядвух товаров задается системой неравенств 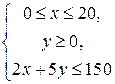 и представляет собой трапецию ОАВС.
и представляет собой трапецию ОАВС.
Кривыми безразличия (линиями постоянной полезности) являются прямые 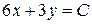 , параллельные прямой
, параллельные прямой 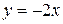 (при
(при 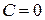 ).
).
Наибольшая полезность потребителя достигается в угловой точке В, лежащей на пересечении прямых 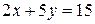 и
и 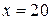 . Точка В имеет координаты (20; 22). Следовательно, объем оптимальной покупки потребителя определяется 20 ед. первого товара и 22 ед. второго товара.
. Точка В имеет координаты (20; 22). Следовательно, объем оптимальной покупки потребителя определяется 20 ед. первого товара и 22 ед. второго товара.
Ответ: 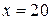 ед.;
ед.; 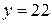 ед.
ед.
 |
Задача 15.полезность потребителя двух товаров, приобретаемых в количествах
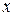 и
и 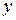 соответственно, задается функцией
соответственно, задается функцией 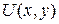 .
. Определить объем оптимальной покупки, если известно: доход потребителя равен 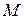 ден. ед., цены на покупаемые товары равны соответственно
ден. ед., цены на покупаемые товары равны соответственно 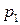 ден. ед. и
ден. ед. и 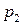 ден. ед. и на рынок поступает не более
ден. ед. и на рынок поступает не более 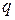 единиц товара i-вида.
единиц товара i-вида.
15.1. 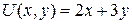 ;
; 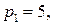
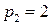 ;
; 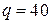 ; i = 2;
; i = 2; 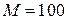 ;
;
15.2. 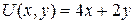 ;
; 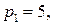
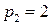 ;
; 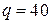 ; i = 2;
; i = 2; 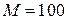 ;
;
15.3. 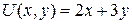 ;
; 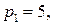
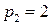 ;
; 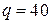 ; i = 1;
; i = 1; 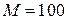 ;
;
15.4. 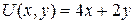 ;
; 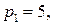
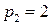 ;
; 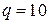 ; i = 1;
; i = 1; 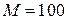 ;
;
15.5. 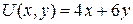 ;
; 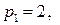
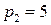 ;
; 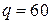 ; i = 2;
; i = 2; 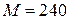 ;
;
15.6. 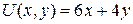 ;
; 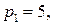
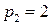 ;
; 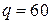 ; i = 2;
; i = 2; 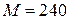 ;
;
15.7. 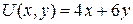 ;
; 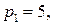
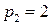 ;
; 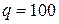 ; i = 1;
; i = 1; 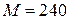 ;
;
15.8. 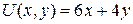 ;
; 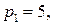
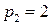 ;
; 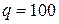 ; i = 1;
; i = 1; 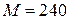 ;
;
15.9. 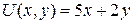 ;
; 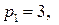
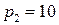 ;
; 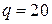 ; i = 2;
; i = 2; 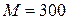 ;
;
15.10. 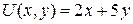 ;
; 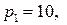
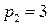 ;
; 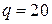 ; i = 1;
; i = 1; 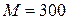 .
.
Пример 16. функция полезности потребителя двух товаров, приобретаемых в количествах 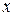 и
и 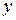 соответственно, имеет вид
соответственно, имеет вид 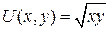 .
.
Определить объем оптимальной покупки, если доход потребителя 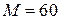 ден. ед., а цены на покупаемые товары равны соответственно
ден. ед., а цены на покупаемые товары равны соответственно 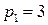 ден. ед. и
ден. ед. и 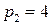 ден. ед.
ден. ед.
Решение. Бюджетное множество потребителядвух товаров задается системой неравенств 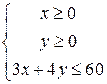 и представляет собой прямоугольный треугольник.
и представляет собой прямоугольный треугольник.
Кривые безразличия (линии постоянной полезности) есть гиперболы 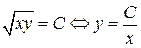 . объем оптимальной покупки достигается в точке касания кривой безразличия бюджетной линии и определяется системой уравнений:
. объем оптимальной покупки достигается в точке касания кривой безразличия бюджетной линии и определяется системой уравнений:
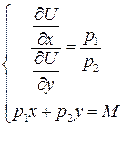 или
или 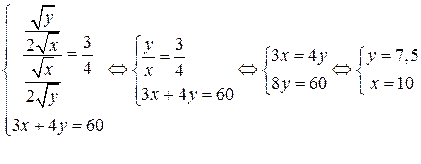 .
.
Ответ: 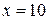 ед.;
ед.; 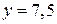 ед.
ед.
Задача 16.функция полезности потребителя двух товаров, приобретаемых в количествах 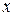 и
и 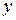 соответственно, имеет вид
соответственно, имеет вид 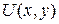 .
.
Определить объем оптимальной покупки, если доход потребителя 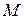 ден. ед., а цены на покупаемые товары равны соответственно
ден. ед., а цены на покупаемые товары равны соответственно 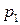 ден. ед. и
ден. ед. и 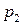 ден. ед.
ден. ед.
16.1. 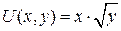 ;
; 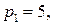
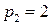 ;
; 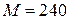 ;
;
16.2. 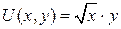 ;
; 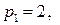
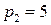 ;
; 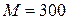 ;
;
16.3. 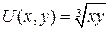 ;
; 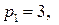
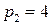 ;
; 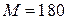 ;
;
16.4. 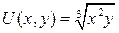 ;
; 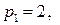
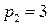 ;
; 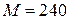 ;
;
16.5. 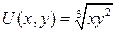 ;
; 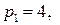
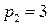 ;
; 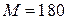 ;
;
16.6. 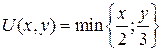 ;
; 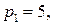
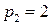 ;
; 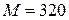 ;
;
16.7. 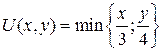 ;
; 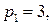
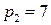 ;
; 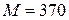 ;
;
16.8. 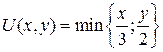 ;
; 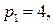
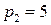 ;
; 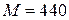 ;
;
16.9. 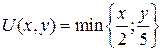 ;
; 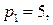
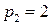 ;
; 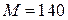 ;
;
16.10. 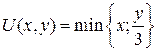 ;
; 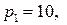
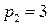 ;
; 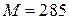 .
.
Пример 17. Функция полных издержек фирмы, производящей товар двух видов в количества x и y, задана соотношением 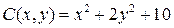 . Цены этих товаров на рынке равны соответственно
. Цены этих товаров на рынке равны соответственно 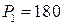 ден. ед. и
ден. ед. и 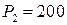 ден. ед.
ден. ед.
Определить, при каких объемах выпуска достигается максимальная прибыль 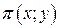 на множестве производственных возможностей, ограниченном издержками производства в объеме
на множестве производственных возможностей, ограниченном издержками производства в объеме 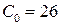 ден. ед.
ден. ед.
Решение. Так как оптимальный выпуск 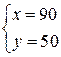 не удовлетворяет условию
не удовлетворяет условию 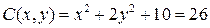 (см. пример 14), то решаем задачу на условный экстремум.
(см. пример 14), то решаем задачу на условный экстремум.
целевой функцией является функция прибыли
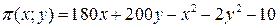 , а уравнением связи
, а уравнением связи 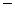 уравнение
уравнение 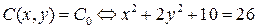 . С учетом последнего получаем, что
. С учетом последнего получаем, что 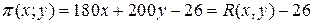 .
.
Для решения задачи на условный экстремум составим систему уравнений
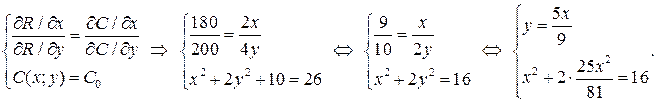 Из последнего уравнения находим
Из последнего уравнения находим 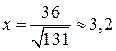 . Тогда
. Тогда 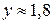 . Таким образом, ограничение на издержки сокращает выпуск продукции и уменьшает прибыль фирмы
. Таким образом, ограничение на издержки сокращает выпуск продукции и уменьшает прибыль фирмы 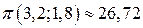 ден. ед. (сравнить с примером 14).
ден. ед. (сравнить с примером 14).
Ответ: 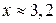 ед.;
ед.; 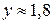 ед.;
ед.; 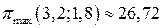 ден. ед.
ден. ед.
Задача 17.Функция полных издержек фирмы, производящей товар двух видов в количества x и y, задана соотношением 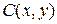 . Цены этих товаров на рынке равны соответственно
. Цены этих товаров на рынке равны соответственно 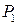 ед. ден. и
ед. ден. и 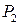 ден. ед.
ден. ед.
Определить, при каких объемах выпуска достигается максимальная прибыль 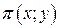 на множестве производственных возможностей, ограниченном издержками производства в объеме
на множестве производственных возможностей, ограниченном издержками производства в объеме 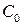 ден. ед., и чему она равна.
ден. ед., и чему она равна.
17.1. 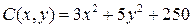 ;
; 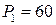
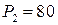 ;
; 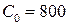 ;
;
17.2. 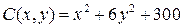 ;
; 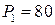 ;
; 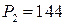 ;
; 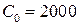 ;
;
17.3. 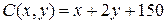 ;
; 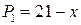 ;
;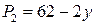 ;
; 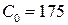 ;
;
17.4. 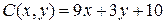 ;
;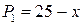 ;
;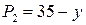 ;
; 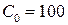 ;
;
17.5. 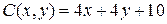 ;
;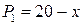 ;
;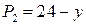 ;
; 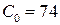 ;
;
17.6. 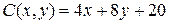 ;
; 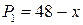 ;
;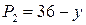 ;
; 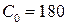 ;
;
17.7. 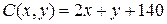 ;
; 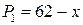 ;
;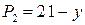 ;
; 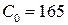 ;
;
17.8. 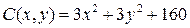 ;
; 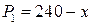 ;
;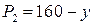 ;
; 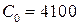 ;
;
17.9. 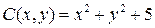 ;
; 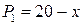 ;
;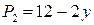 ;
; 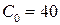 ;
;
17.10. 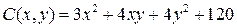 ;
;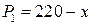 ;
; 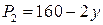 ;
; 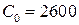 .
.
Пример 18.1. Производственная функция однопродуктовой фирмы задана соотношением 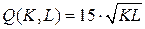 .
.
Вычислить оптимальный объём выпуска продукции, если издержки не могут превышать 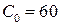 ден. ед. и известны цены на ресурсы:
ден. ед. и известны цены на ресурсы: 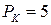 ден. ед. и
ден. ед. и 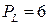 ден. ед.
ден. ед.
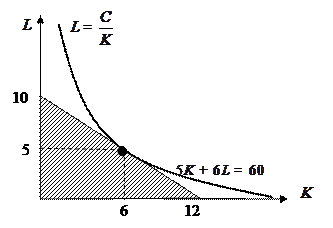 |
Решение. в точке оптимального объема выпуска изокванта (линия постоянного выпуска) касается изокосты (линии постоянных издержек),
что позволяет составить систему уравнений
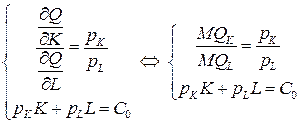 или
или
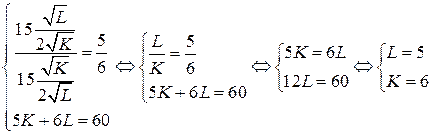 .
.
оптимальный объём выпуска продукции составляет 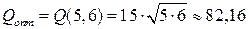 ед.
ед.
Ответ: 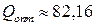 ед.
ед.
Пример 18.2. Производственная функция однопродуктовой фирмы задана соотношением 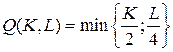 .
.
Вычислить оптимальный объём выпуска продукции, если издержки не могут превышать 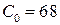 ден. ед. и известны цены на ресурсы:
ден. ед. и известны цены на ресурсы: 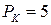 ден. ед. и
ден. ед. и 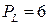 ден. ед.
ден. ед.
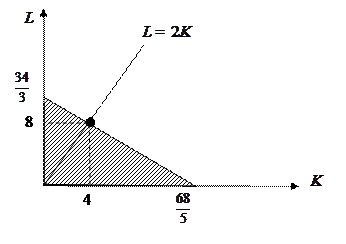 |
Решение. Изокванты производственной функции
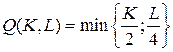 представляют собой «уголки», скользящие по прямой
представляют собой «уголки», скользящие по прямой 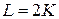 (см. пример 10.2).
(см. пример 10.2). Ресурсы, необходимые для производства оптимального объёма выпуска продукции, определяются точкой пересечения этой прямой 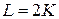 с изокостой (линией постоянных издержек)
с изокостой (линией постоянных издержек) 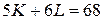 .
.
Решая систему линейных уравнений 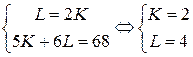 , находим объемы ресурсов, необходимые для оптимального объема выпуска фирмы. Тогда
, находим объемы ресурсов, необходимые для оптимального объема выпуска фирмы. Тогда 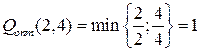 .
.
Ответ: 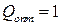 ед.
ед.
Задача 18. задана производственная функция однопродуктовой фирмы 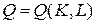 .
.
Вычислить оптимальный объём выпуска продукции, если издержки не могут превышать 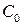 ден. ед. и известны цены на ресурсы:
ден. ед. и известны цены на ресурсы: 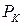 ден. ед. и
ден. ед. и 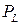 ден. ед.
ден. ед.
18.1. 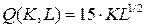 ;
; 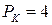 ;
; 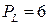 ;
; 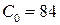 ;
;
18.2. 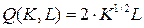 ;
; 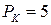 ;
; 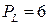 ;
; 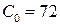 ;
;
18.3. 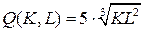 ;
; 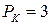 ;
; 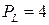 ;
; 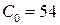 ;
;
18.4. 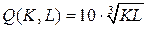 ;
; 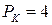 ;
; 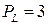 ;
; 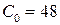 ;
;
18.5. 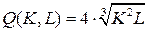
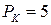 ;
; 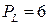 ;
; 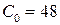 ;
;
18.6. 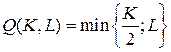 ;
; 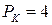 ;
; 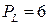 ;
; 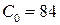 ;
;
18.7. 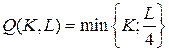 ;
; 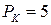
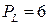 ;
; 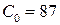 ;
;
18.8. 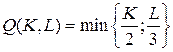 ;
; 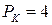 ;
; 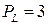 ;
; 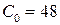 ;
;
18.9. 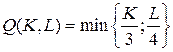 ;
; 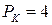 ;
; 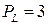 ;
; 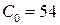 ;
;
18.10. 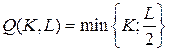 ;
; 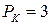
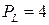 ;
; 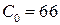 ;
;
18. 11. 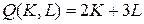 ;
; 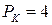 ;
; 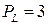 ;
; 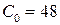 ;
;
18.12. 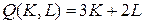 ;
; 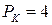 ;
; 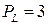 ;
; 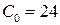 ;
;
18.13. 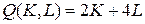 ;
; 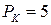 ;
; 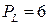 ;
; 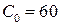 ;
;
18.14. 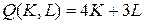 ;
; 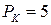
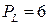 ;
; 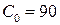 ;
;
18.15. 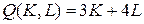 ;
; 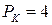
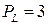 ;
; 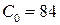 .
.
